Презентация, доклад по теме Качественные задачи ЕГЭ. Механика.

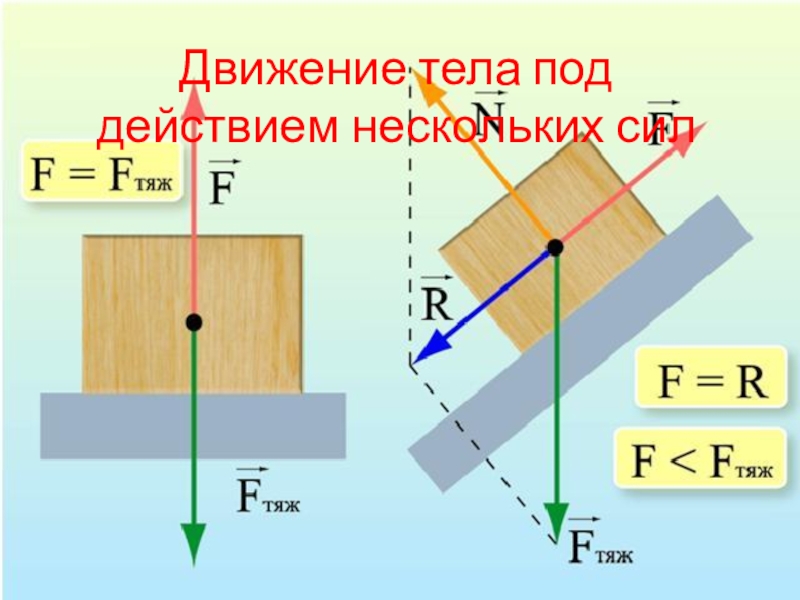
Брусок массой m кладут на плоскость, наклонённую под углом α к горизонту, и отпускают с начальной скоростью равной нулю. Коэффициент трения между бруском и плоскостью равен μ . При каких α брусок будет съезжать по плоскости? Чему равна при этом сила трения бруска о плоскость?



Решение. При равномерном скольжении Fтр = mgx = mgsin α , mgy = N,
Fтр = μN = μ mgcos α. mgsin α= μ mgcos α, μ= sinα / cos α = tg α.
α = arctg μ.
Брусок начнёт съезжать с наклонной плоскости при условии α > arctg μ.
Сила трения равна Fтр = μ mgcos α.

Деревянный брусок плавает на поверхности воды в миске. Миска покоится на поверхности Земли. Что произойдет с глубиной погружения бруска в воду, если миска будет стоять на полу лифта, который движется с ускорением, направленным вертикально вверх? Ответ поясните, используя физические закономерности.
Решение: По второму закону Ньютона, ma = FА – mg (1), где m – масса бруска,  FA  — Архимедова сила, равная весу вытесненной бруском воды: FA  = mж(g + a) = ρVж(g + a) (2). Жидкости практически несжимаемы, поэтому плотность воды не зависит от ускорения и остается постоянной при любом движении описанной системы. В покоящемся лифте ρgV = mg (3), а в движущемся, с учетом (1),  ρV1(g + a ) = m(g + a) (4).  Из выражения (4), получаем, что ρV1 = m, и, сравнивая его с (3), заключаем, что V1 = V, т.е. глубина погружения бруска не изменится.