- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Правильные многоугольники (9 класс)
Содержание
- 1. Презентация по геометрии на тему Правильные многоугольники (9 класс)
- 2. Определите , какую величину можно найти, используя
- 3. Реши устно задачи:Сторона правильного шестиугольника равна
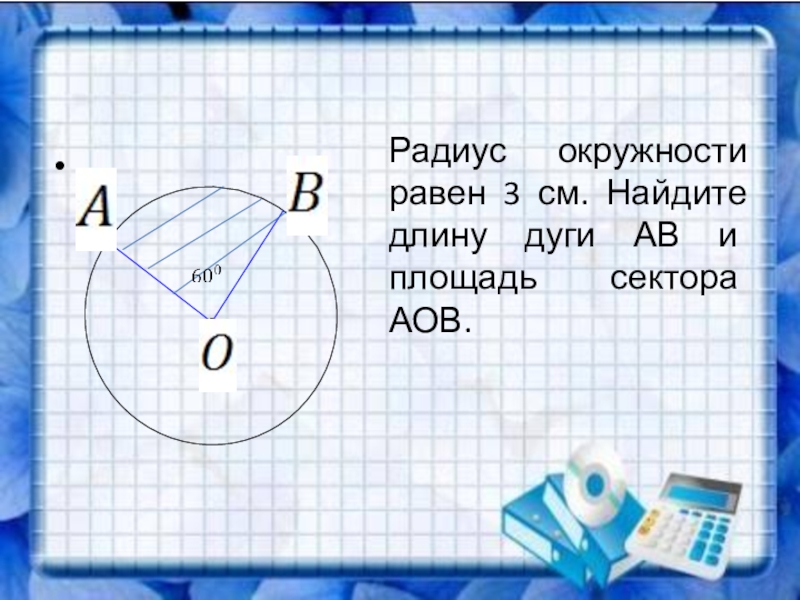
- 4. Радиус окружности равен 3 см. Найдите длину дуги АВ и площадь сектора АОВ.
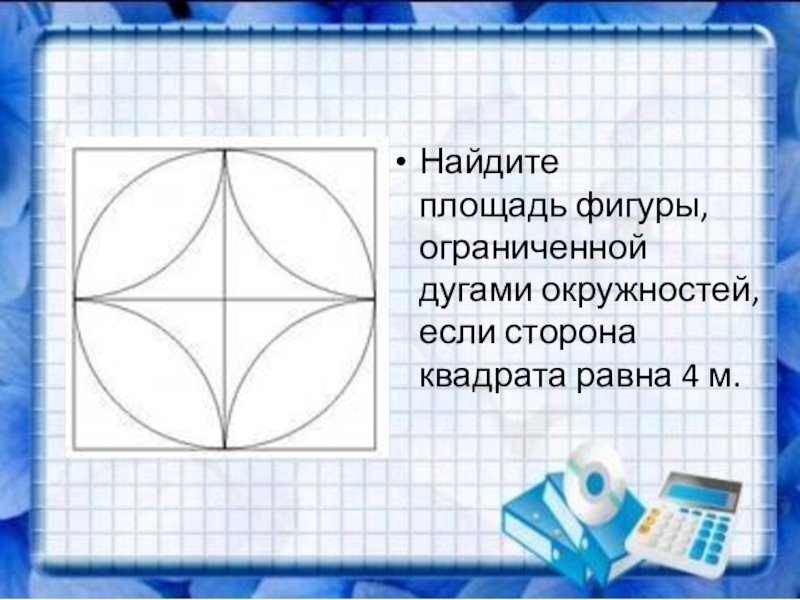
- 5. Найдите
- 6. Найдите площадь кольца, если радиус большей окружности равен 5 дм, а радиус меньшей- 4 дм.
- 7. Самостоятельная работа№1104(б),№1119№1104(а),№1117 (а)
- 8. Решение A
- 9. Самостоятельная работаРешениеО- центр описанной окружности и середина
- 10. Слайд 10
Определите , какую величину можно найти, используя это выражение сSrSn anSSαLсαn
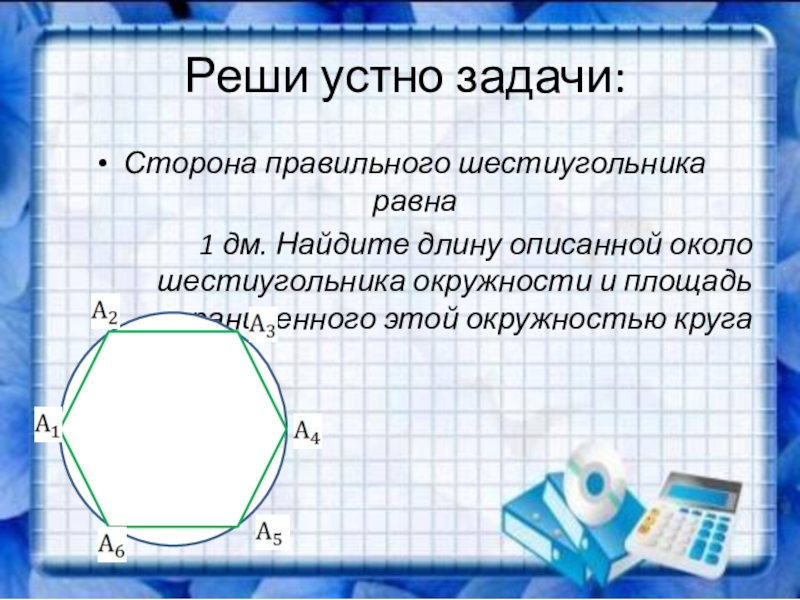
Слайд 3 Реши устно задачи:
Сторона правильного шестиугольника равна
1 дм. Найдите длину
описанной около шестиугольника окружности и площадь ограниченного этой окружностью круга
Слайд 9Самостоятельная работа
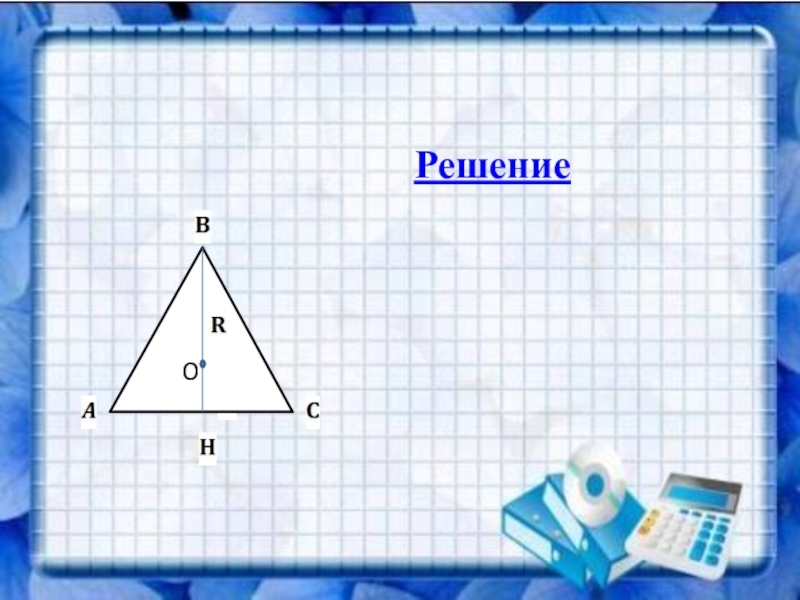
Решение
О- центр описанной окружности и середина гипотенузы AB
Тогда OA= OB=R
=
№ 1104 (б)
С= 2π= π2R= π
O