- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по физикеГород доступная среда(на примере пандусов)
Содержание
- 1. Презентация по физикеГород доступная среда(на примере пандусов)
- 2. Проект выполнен учащимися 10 класса школы
- 3. Цель и задачи проектаЦель проекта: раскрыть проблему
- 4. НАКЛОННАЯ ПЛОСКОСТЬ Наклонная плоскость применяется для перемещения
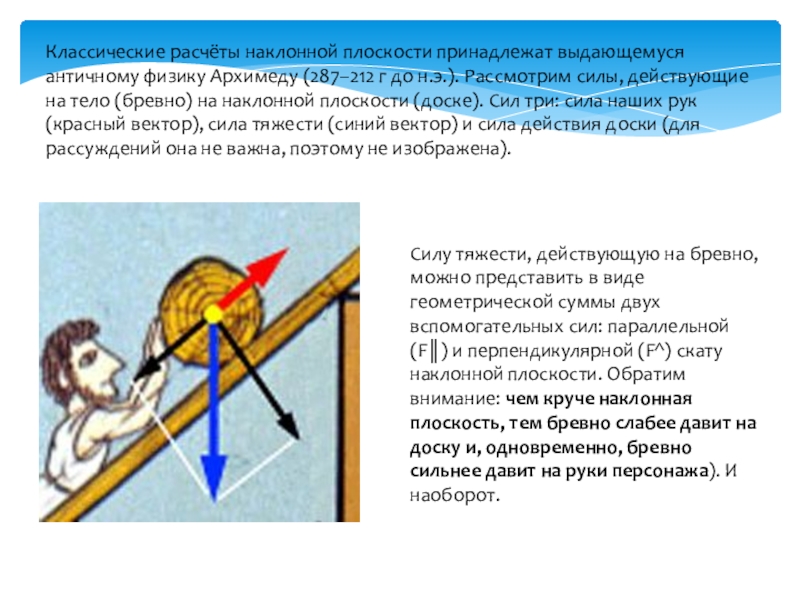
- 5. Классические расчёты наклонной плоскости принадлежат выдающемуся античному
- 6. условие равновесия сил на наклонной плоскостиРисунок на
- 7. Если не учитывать силу трения, то расчёты
- 8. Очень остроумно использована наклонная плоскость на Красноярской
- 9. А почему горные дороги вьются пологим "серпантином"?
- 10. Это международный документ, согласно которому все страны
- 11. Одна из важнейших характеристик пандуса — уклон. Если наклонные поверхности пандуса
- 12. Уклон пандуса может быть выражен в градусах, процентах и в виде отношения высоты к длине
- 13. Пандус для маломобильных групп Нормативный угол наклона пандуса
- 14. Исследование зависимости силы тяги наклонной плоскости от
- 15. Запишем второй закон Ньютона для равномерного движенияFтяг
- 16. Вывод:По результатам измерений видно, что чем больше
- 17. Роль силы трения покоя Исследования показали, что
- 18. Почему люди самостоятельно не могут воспользоваться некоторыми
- 19. Исследование зависимости КПД наклонной плоскости от угла
- 20. Если трение отсутствует, то коэффициент трения μ
- 21. Результаты измерений и расчетовВывод: Чем больше угол
- 22. Измеряем длину пандуса рулеткойОна оказалась 6,4м, что
- 23. Мозговой штурмКак практически определить высоту пандуса, если прямые измерения невозможны?
- 24. Решение проблемы1. Измерить высоты ступенек и найти
- 25. Слайд 25
- 26. Измеряем среднюю линию пандуса . Она оказалась
- 27. Результаты проверки соответствия уклона пандуса принятым стандартам
- 28. Длина пандуса и максимальный коэффициент трения покоя
- 29. Учитывая недостаточное пространство у входа в школу
- 30. ЛитератураЛ.Э. Генденштейн, Ю.И. Дик Учебник физики 10
- 31. Спасибо за внимание
Слайд 1Проект
«Город-доступная среда обитания»
Работу выполнили ученики 10 класса Г
ГБОУ школа
Руководитель Гречихина Т.С.
Слайд 2Проект выполнен учащимися 10 класса школы
№ 1741, 2-ое подразделение
Руководители проекта:
Учитель
Учитель математики Балашова Елена Георгиевна
Москва 2018г
Слайд 3Цель и задачи проекта
Цель проекта: раскрыть проблему города как доступной среде
Задачи проекта:
1. Ответить на вопрос: почему люди самостоятельно не могут воспользоваться некоторыми пандусами?
2. Исследовать получение выигрыша в силе с помощью наклонной плоскости, роль силы трения при подъеме по наклонной плоскости.
3.Выяснить соответствие пандусов у школы государственным стандартам.
Слайд 4НАКЛОННАЯ ПЛОСКОСТЬ
Наклонная плоскость применяется для перемещения тяжелых предметов на более высокий
. Сегодня примерами наклонных плоскостей являются трапы, пандусы, эскалаторы, конвейеры, а также горный «серпантин» автомобильных дорог. Все эти наклонные плоскости применяются для того, чтобы облегчить подъём на высоту.
Слайд 5Классические расчёты наклонной плоскости принадлежат выдающемуся античному физику Архимеду (287–212 г
Силу тяжести, действующую на бревно, можно представить в виде геометрической суммы двух вспомогательных сил: параллельной (F║) и перпендикулярной (F^) скату наклонной плоскости. Обратим внимание: чем круче наклонная плоскость, тем бревно слабее давит на доску и, одновременно, бревно сильнее давит на руки персонажа). И наоборот.
Слайд 6условие равновесия сил на наклонной плоскости
Рисунок на титульном листе книги С.
"Тело на наклонной плоскости удерживается силой, которая ... по величине во столько раз меньше веса этого тела, во сколько раз длина наклонной плоскости больше ее высоты".
Условие равновесия сил на наклонной плоскости сформулировал голландский ученый Симон Стевин (1548-1620).
Слайд 7Если не учитывать силу трения, то расчёты (или измерения) показывают: если
Слайд 8Очень остроумно использована наклонная плоскость на Красноярской ГЭС. Здесь вместо шлюзов
Слайд 10Это международный документ, согласно которому все страны – участники обязаны соблюдать
Конвенция ООН по правам инвалидов.
Слайд 11Одна из важнейших характеристик пандуса — уклон.
Если наклонные поверхности пандуса выполнены с уклоном, превышающим нормы —
Слайд 13Пандус для маломобильных групп
Нормативный угол наклона пандуса для колясок должен быть не более 1:20
Слайд 14Исследование зависимости силы тяги наклонной плоскости от угла ее наклона к
Оборудование: трибометр, брусок, линейка ученическая.
Измеряем силу тяги при
различных углах наклона
Слайд 15Запишем второй закон Ньютона для равномерного движения
Fтяг + Fmp + N
В проекции на оси координат после несложных преобразований получим:
Fтяг = mg(sinα + μcosα).
Если трение отсутствует, то μ = 0 и тогда
Fтяг = mgsinα.
Эту силу называют скатывающей силой
Слайд 16Вывод:
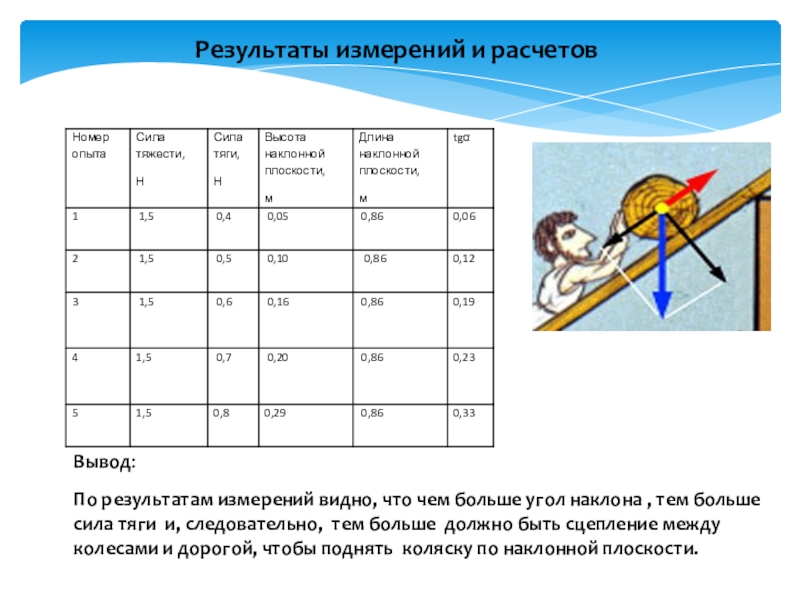
По результатам измерений видно, что чем больше угол наклона , тем
Результаты измерений и расчетов
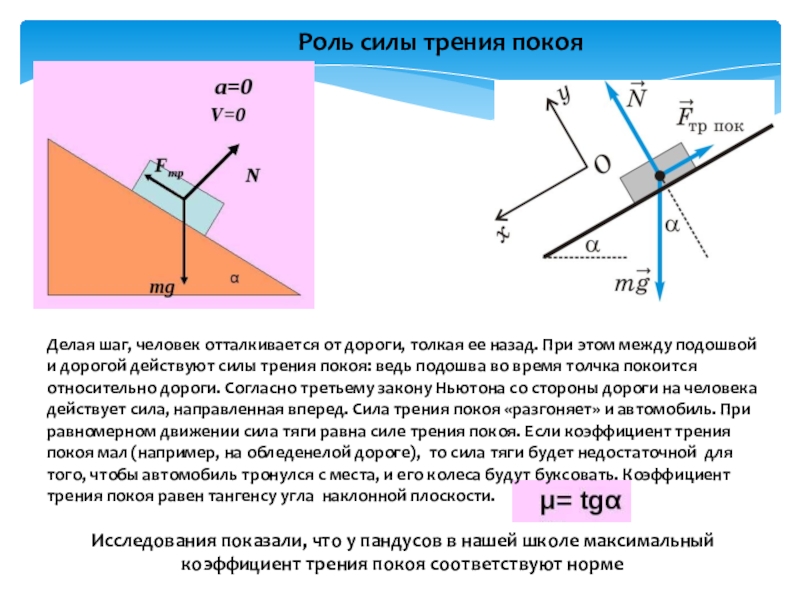
Слайд 17Роль силы трения покоя
Исследования показали, что у пандусов в нашей
Делая шаг, человек отталкивается от дороги, толкая ее назад. При этом между подошвой и дорогой действуют силы трения покоя: ведь подошва во время толчка покоится относительно дороги. Согласно третьему закону Ньютона со стороны дороги на человека действует сила, направленная вперед. Сила трения покоя «разгоняет» и автомобиль. При равномерном движении сила тяги равна силе трения покоя. Если коэффициент трения покоя мал (например, на обледенелой дороге), то сила тяги будет недостаточной для того, чтобы автомобиль тронулся с места, и его колеса будут буксовать. Коэффициент трения покоя равен тангенсу угла наклонной плоскости.
Слайд 18Почему люди самостоятельно не могут воспользоваться некоторыми пандусами?
Допустим, ребенок вместе с
Силу тяги. Fтяг = mg(sinα + μcosα).
Вычислим, какую силу нужно приложить, чтобы по пандусу в коляске
подняться к нам в школу.
Из данных справочника по физике и технике узнали коэффициент трения качения - 0,02.
Fтяг. = 60*10(0,175+0,02*0,98) =120Н
У входа в школу со двора:
У входа в школу с улицы:
Fтяг. = 60*10(0,44+0,02*0,98) =384Н
Это равнозначно тому, чтобы нести сумку массой 38 кг.
Это равнозначно тому, чтобы нести сумку массой 12 кг
Слайд 19Исследование зависимости КПД наклонной плоскости от угла ее наклона к горизонту.
Оборудование:
Как известно, КПД наклонной плоскости (рис.)
η = (An/Ac)•100 %,
где Аn = Fтягl − полезная работа, т. е. работа по равномерному подъему тела без трения (l − длина наклонной плоскости), а Ас = Fтягl − работа при наличии трения (совершенная работа).
Запишем второй закон Ньютона для равномерного движения
Fтяг + Fmp + N + mg = 0 (в векторном виде).
В проекции на оси координат после несложных преобразований получим:
Fтяг = mg(sinα + μcosα).
Слайд 20Если трение отсутствует, то коэффициент трения μ = 0 и тогда
Fтяг
Таким образом,
η = sinα/(sinα + μcosα),
или
η = 1/(1 + μctgα).
Отсюда следует, что для того, чтобы найти η (КПД) как функцию угла α, надо знать коэффициент трения μ. Для определения μ подберем угол наклона α0 трибометра (наклонной плоскости) таким образом, чтобы брусок двигался вниз с небольшим ускорением. Тогда
l = at2/2. (1)
Длину наклонной плоскости l измеряем линейкой. Время движения определим по секундомеру.
Из выражения (1) имеем: ускорение
а = 2l/t2. (2)
Из второго закона Ньютона уравнение движения:
ma = mgsinα0 − μmgcosα0. (3)
совместное решение уравнений (2) и (3) дает:
μ = (gsinαo − 2l/t2)/(gcosαo). (4)
Преобразовав выражение (4), имеем:
μ = tgαo − 2l/(gt2cosαo).
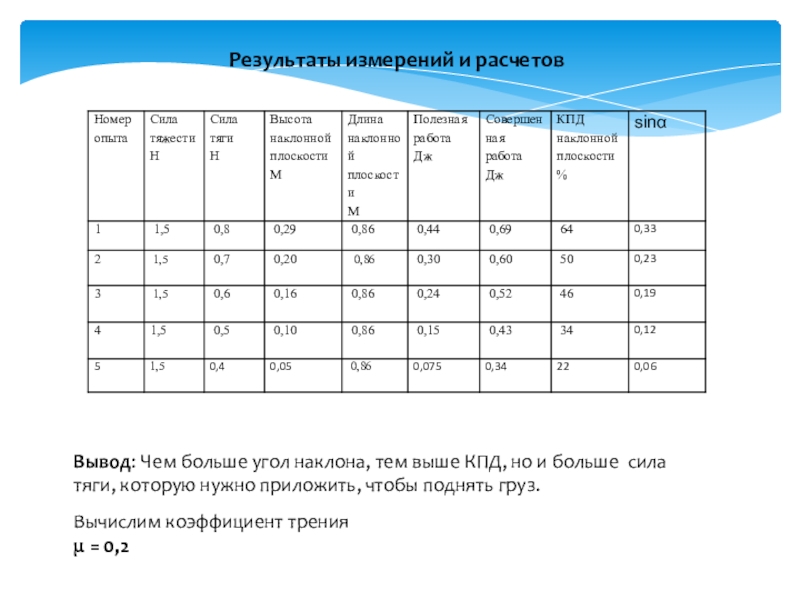
Слайд 21Результаты измерений и расчетов
Вывод: Чем больше угол наклона, тем выше КПД,
Вычислим коэффициент трения
μ = 0,2
Слайд 22Измеряем длину пандуса рулеткой
Она оказалась 6,4м, что соответствует норме (длина одного
Вход в нашу школу
Слайд 24Решение проблемы
1. Измерить высоты ступенек и найти их сумму
2.На стене здания
параллельную дороге, и измерить высоту
3.Использовать свойства средней линии треугольника
Выбираем последнее решение
Слайд 26Измеряем среднюю линию пандуса .
Она оказалась 56 см.
Высота пандуса
на основе свойства средней линии
Слайд 28Длина пандуса и максимальный коэффициент трения покоя соответствуют норме
Уклон пандуса при
Уклон пандуса при входе в школу с улицы превышает нормативный угол наклона в 9 раз
Вывод
Слайд 29Учитывая недостаточное пространство у входа в школу предлагаем изменить форму пандуса,
Предложения
Слайд 30Литература
Л.Э. Генденштейн, Ю.И. Дик Учебник физики 10 класс
Б.М. Яворский Основы физики
А.С.
Интернет - ресурсы