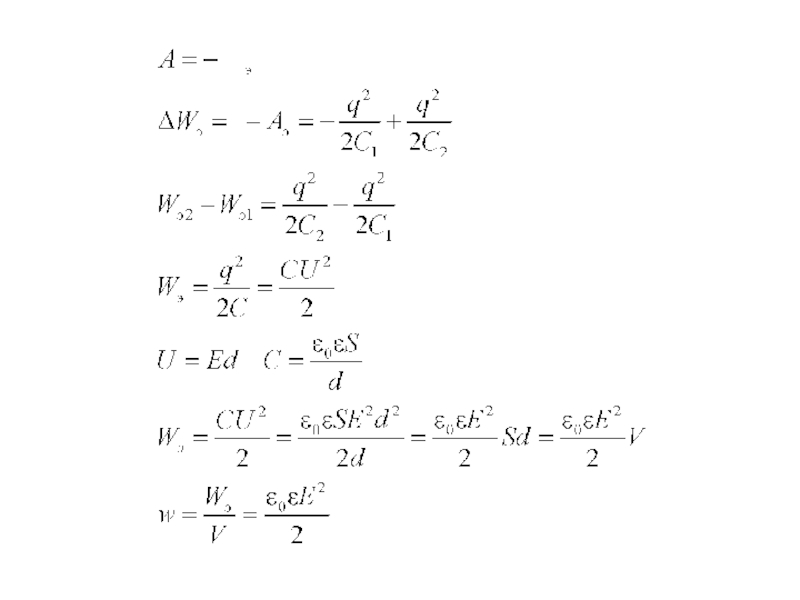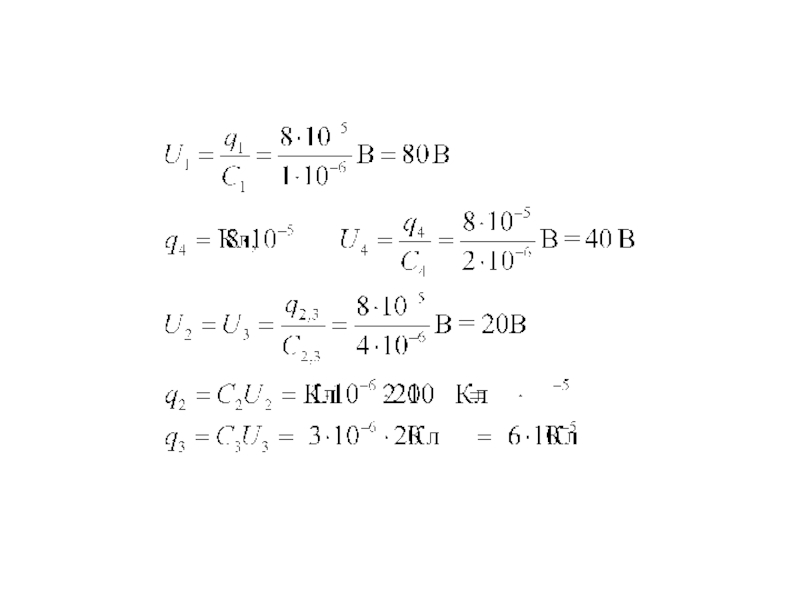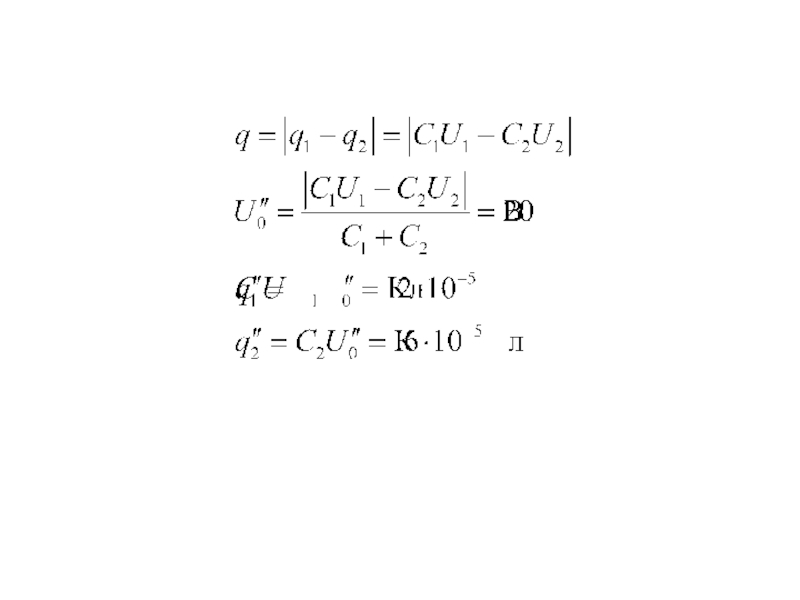- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по физике на темуРазность потенциалов, потенциал
Содержание
- 1. Презентация по физике на темуРазность потенциалов, потенциал
- 2. Работа электростатической силы по перемещению заряда
- 3. Слайд 3
- 4. ПотенциалПотенциалом в данной точке поля называется отношение
- 5. Потенциал в данной точке поля равен потенциальной
- 6. Эквипотенциальные поверхностиГеометрическое место точек, имеющих одинаковый потенциал, называется эквипотенциальной поверхностью.
- 7. Силовые линии перпендикулярны эквипотенциальным поверхностям. А1
- 8. Принцип суперпозиции для потенциалаПотенциал поля диполя
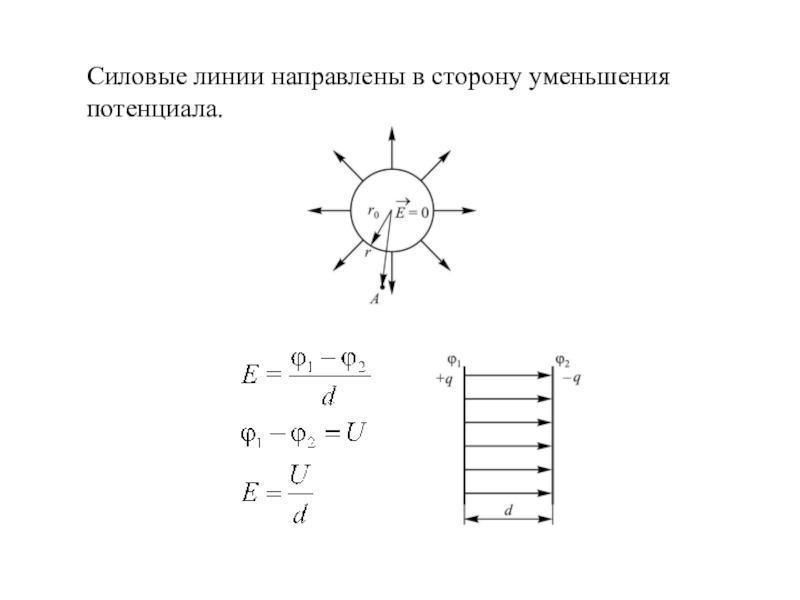
- 9. Связь напряженности электрического поля с потенциалом
- 10. Силовые линии направлены в сторону уменьшения потенциала.
- 11. Примеры решения задачЗамечания:1) если поле создается заряженными
- 12. Задача 1. Одинаковые одноименные точечные заряды 4
- 13. Задача 2. На расстоянии l = 40
- 14. Задача 3. В центре металлической сферической оболочки
- 15. Слайд 15
- 16. Задача 4. Проводящую сферу радиусом 20 см
- 17. Задача 5. Два одинаковых шарика, имеющих одинаковые
- 18. Задача 6. Протон с начальной скоростью υ0
- 19. Задача 7. Два небольших проводящих заряженных шара
- 20. Задача 8. N одинаковых сферических капелек ртути
- 21. Слайд 21
- 22. Электроемкость. Энергия электрического поляЭлектроемкость уединенного проводника
- 23. Электроемкость конденсатора
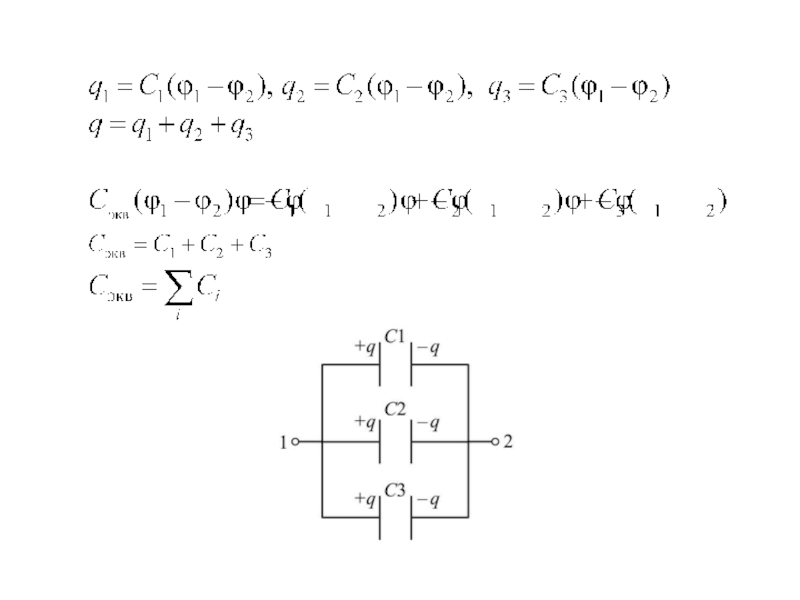
- 24. Последовательное и параллельное соединение конденсаторов
- 25. Слайд 25
- 26. Энергия электрического поля1. Плоский конденсатор.
- 27. Слайд 27
- 28. 2. Энергия системы проводников.
- 29. Примеры решения задачСоединение конденсаторовПлан решения задач 1)
- 30. Задача 1. Четыре конденсатора электроемкостями С1 =
- 31. Слайд 31
- 32. Задача 2. Определите эквивалентную электрическую емкость
- 33. Задача 3. Определите электроемкость системы конденсаторов, изображенной
- 34. Задача 4. Определите емкость системы, изображенной на
- 35. Задача 5. Конденсатор электроемкостью С1 = 1
- 36. Слайд 36
- 37. Задача 6. Энергия плоского воздушного конденсатора
- 38. Задача 7. Пластины плоского конденсатора подключены к
- 39. Задача 8. В плоский воздушный конденсатор вставляется
- 40. Задача 9. Определите изменение заряда проводящей сферы
Работа электростатической силы по перемещению заряда
Слайд 4Потенциал
Потенциалом в данной точке поля называется отношение работы электростатической силы по
перемещению положительного заряда из данной точки на бесконечность к величине этого заряда.
Слайд 5Потенциал в данной точке поля равен потенциальной энергии, которой обладает единичный
положительный заряд, помещенный в эту точку поля:
Wпот + Wкин = const
Слайд 6Эквипотенциальные поверхности
Геометрическое место точек, имеющих одинаковый потенциал, называется эквипотенциальной поверхностью.
Слайд 7Силовые линии перпендикулярны эквипотенциальным поверхностям.
А1 2 = q (1
– 2), 1 = 2, А1 2 = 0
А = qEr cos
cos = 0, = π/2
А = qEr cos
cos = 0, = π/2
Поверхность проводника всегда является эквипотенциальной поверхностью. Внутри проводника потенциал постоянен и равен потенциалу поверхности.
Слайд 11Примеры решения задач
Замечания:
1) если поле создается заряженными проводниками, то необходимо учесть,
что внутри проводника напряженность равна нулю, а потенциал постоянен;
2) если проводник заземлен, то потенциал проводника равен нулю, заряд же может быть отличен от нуля.
2) если проводник заземлен, то потенциал проводника равен нулю, заряд же может быть отличен от нуля.
Слайд 12Задача 1. Одинаковые одноименные точечные заряды 4 10-7 Кл расположены
в двух вершинах равностороннего треугольника
со стороной а = 1 м. Определите значение напряженности
и потенциала в третьей вершине А треугольника.
Решение.
Решение.
Слайд 13Задача 2. На расстоянии l = 40 см от поверхности заряженного
металлического шарика радиусом r = 10 см помещен точечный заряд q2 = 8 10-9 Кл. Заряд шарика
q1 = 4 10-9 Кл. Определите потенциал шарика.
Решение.
Решение.
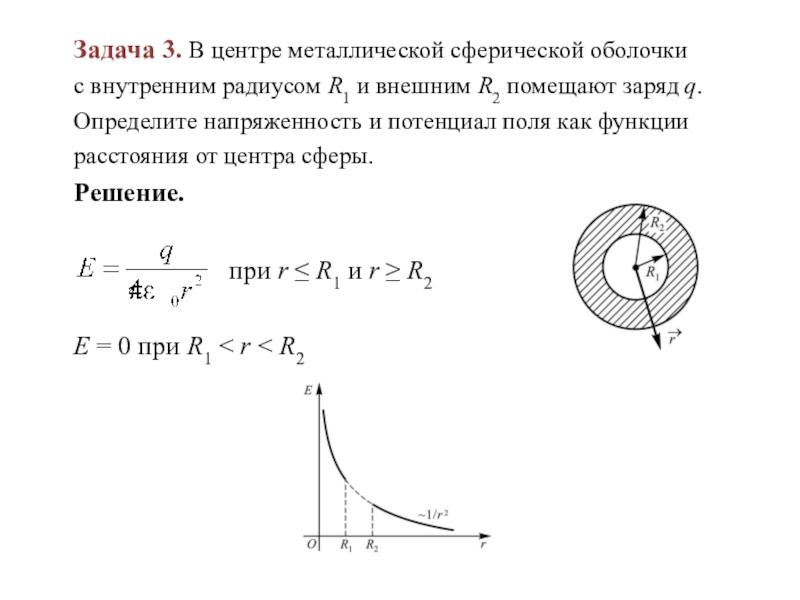
Слайд 14Задача 3. В центре металлической сферической оболочки с внутренним радиусом R1
и внешним R2 помещают заряд q. Определите напряженность и потенциал поля как функции расстояния от центра сферы.
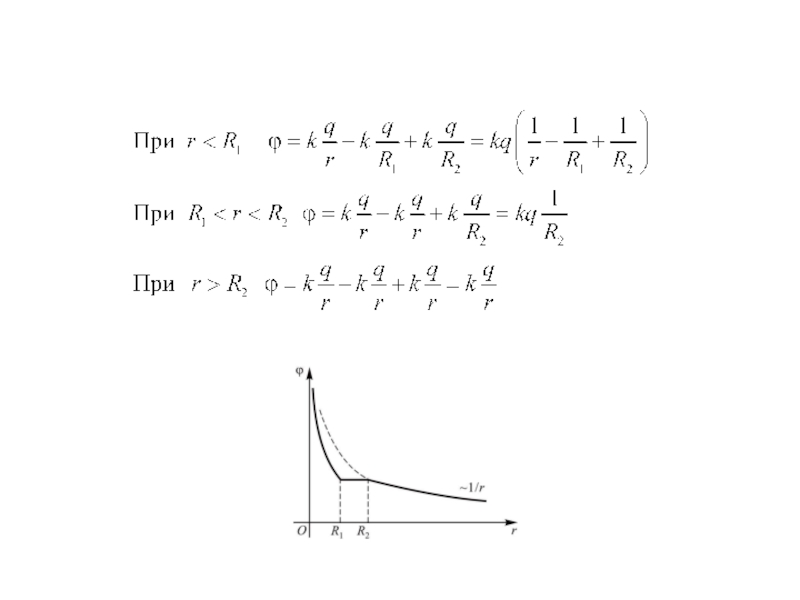
Решение.
Е = 0 при R1 < r < R2
Решение.
Е = 0 при R1 < r < R2
при r R1 и r R2
Слайд 16Задача 4. Проводящую сферу радиусом 20 см окружили тонкой сферической оболочкой
радиусом 40 см и с зарядом 2 10-6 Кл. Определите заряд сферы после того, как ее заземлили, а также потенциал оболочки.
Решение.
Решение.
Слайд 17Задача 5. Два одинаковых шарика, имеющих одинаковые одноименные заряды, соединены пружиной,
жесткость которой
k = 20 Н/м, а длина l0 = 4 см. Шарики колеблются так,
что расстояние между ними меняется от 3 см до 6 см.
Найдите заряды шариков.
Решение.
Решение.
Слайд 18Задача 6. Протон с начальной скоростью υ0 летит прямо на первоначально
покоящееся ядро гелия. Каковы скорости частиц в тот момент, когда расстояние между ними минимально? Считать, что масса ядра гелия равна учетверенной массе протона.
Решение.
Решение.
Слайд 19Задача 7. Два небольших проводящих заряженных шара радиуса r расположены на
расстоянии l друг от друга (l >> 2r). Шары поочередно на некоторое время заземляют.
Определите потенциал шара, который был заземлен первым. Первоначально каждый шар имел заряд q.
Решение.
Решение.
Слайд 20Задача 8. N одинаковых сферических капелек ртути заряжены до одного и
того же потенциала 0. 1) Каким будет потенциал большой капли, если все капли сольются в одну? 2) Оцените,
при каких значениях зарядов капель это может произойти?
Решение.
Решение.
Слайд 29Примеры решения задач
Соединение конденсаторов
План решения задач
1) Делаем рисунок.
2) Определяем последовательно
и параллельно соединенные конденсаторы. Напоминаем, что признаком последовательного соединения является равенство заряда, а параллельного одинаковая разность потенциалов.
3) Если соединения неочевидны, то находим точки схемы, потенциалы которых равны.
4) Соединяем эти точки или не учитываем наличие конденсатора, присоединенного к этим точкам, т.к. он не накапливает электрический заряд.
5) Рисуем эквивалентную схему, которую используем для расчета Сэкв.
3) Если соединения неочевидны, то находим точки схемы, потенциалы которых равны.
4) Соединяем эти точки или не учитываем наличие конденсатора, присоединенного к этим точкам, т.к. он не накапливает электрический заряд.
5) Рисуем эквивалентную схему, которую используем для расчета Сэкв.
Слайд 30Задача 1. Четыре конденсатора электроемкостями С1 = 1 мкФ, С2 =
1 мкФ, С3 = 3 мкФ, С4 = 2 мкФ соединены, как показано
на рисунке. К точкам А и В подводится напряжение U = 140 В. Найдите заряд и напряжение на каждом из конденсаторов.
Решение.
Решение.
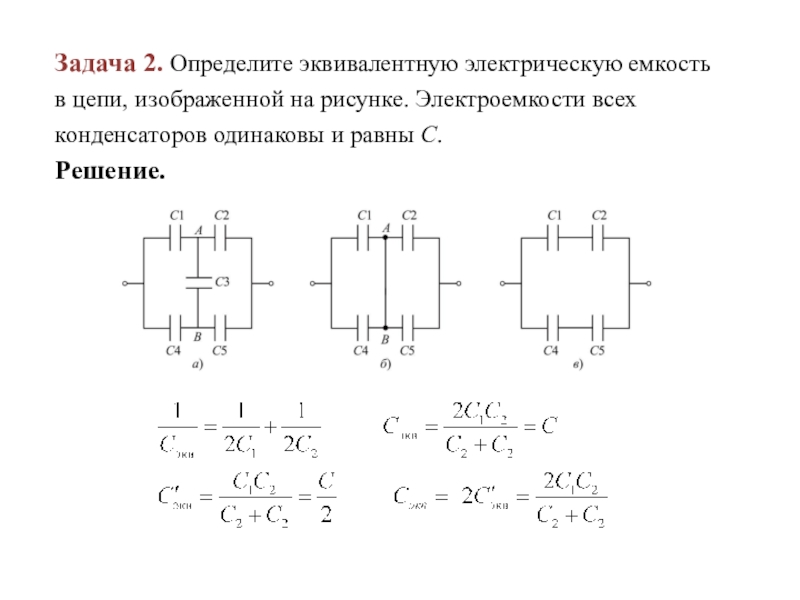
Слайд 32Задача 2. Определите эквивалентную электрическую емкость в цепи, изображенной на рисунке.
Электроемкости всех конденсаторов одинаковы и равны С.
Решение.
Решение.
Слайд 33Задача 3. Определите электроемкость системы конденсаторов, изображенной на рисунке, если разность
потенциалов подводится к точкам а) A, D; б) В, D.
Решение.
а) B = E
б) А = E
Сэкв2 = 2С
Решение.
а) B = E
б) А = E
Сэкв2 = 2С
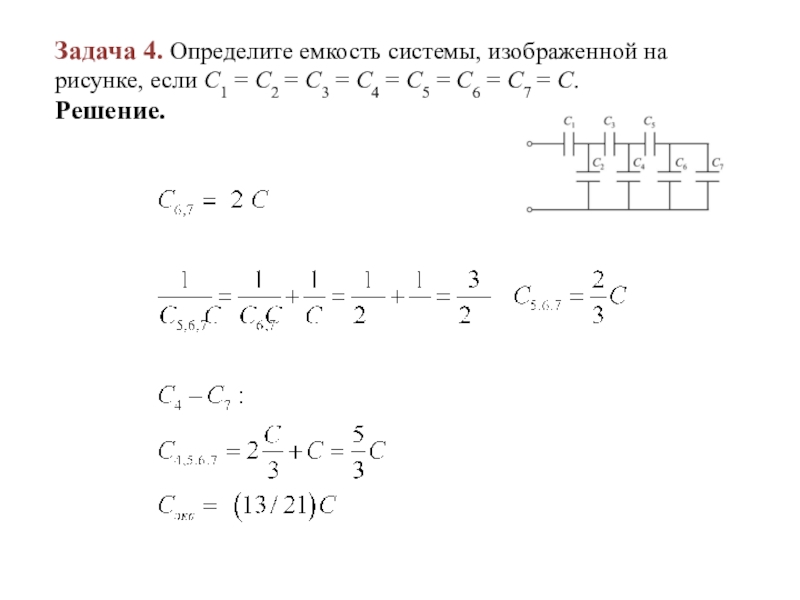
Слайд 34Задача 4. Определите емкость системы, изображенной на рисунке, если C1 =
С2 = С3 = С4 = С5 = С6 = С7 = С.
Решение.
Решение.
Слайд 35Задача 5. Конденсатор электроемкостью С1 = 1 мкФ, заряженный до разности
потенциалов U1 = 100 В и отключенный от источника, соединили параллельно с конденсатором электроемкостью С2 = 3 мкФ, заряженным до разности потенциалов U2 = 60 В. Определите заряд каждого
из конденсаторов и разность потенциалов между обкладками после их соединения, если
1) соединяются обкладки, имеющие одноименные заряды;
2) соединяются обкладки, имеющие разноименные заряды.
Решение.
1) соединяются обкладки, имеющие одноименные заряды;
2) соединяются обкладки, имеющие разноименные заряды.
Решение.
Слайд 37Задача 6. Энергия плоского воздушного конденсатора W1 = 2 10-7
Дж. Определите энергию конденсатора после заполнения его диэлектриком с диэлектрической проницаемостью = 2, если:
1) конденсатор отключен от источника питания;
2) конденсатор подключен к источнику питания.
Решение.
1) конденсатор отключен от источника питания;
2) конденсатор подключен к источнику питания.
Решение.
Слайд 38Задача 7. Пластины плоского конденсатора подключены к источнику U = 2 В.
Определите изменение емкости и энергии электрического поля конденсатора, если конденсатор наполовину заполнен диэлектриком с диэлектрической проницаемостью = 2. Расстояние между пластинами d = 1 см, площадь пластин S = 50 см2.
Решение.
Решение.
Слайд 39Задача 8. В плоский воздушный конденсатор вставляется металлическая пластина толщиной d0.
Заряд на обкладках конденсатора q. Конденсатор отключен от источника. Расстояние между пластинами d, площадь пластин S. Определите изменение электроемкости конденсатора и энергии его электрического поля, если конденсатор не подключен к источнику.
Решение.
Решение.
Слайд 40Задача 9. Определите изменение заряда проводящей сферы радиуса 10 см, первоначально
заряженной до потенциала 104 В, если с течением времени она частично потеряла заряд и ее энергия уменьшилась на 1,5 10-4 Дж.
Решение.
Решение.