- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по физике на тему Механические колебания (11 класс)
Содержание
- 1. Презентация по физике на тему Механические колебания (11 класс)
- 2. Колебания - один из самых распространенных процессов
- 3. СВОБОДНЫЕ – колебания, возникающие в системе
- 4. УСЛОВИЯ ВОЗНИКНОВЕНИЯ СВОБОДНЫХ КОЛЕБАНИЙ при выведении тела
- 5. Уравнение движение груза, подвешенного на пружине
- 6. Уравнение движения математического маятникаУравнение движения математического маятникаМатематический
- 7. xm – модуль максимального смещения точки
- 8. φ – фаза колебаний, которая определяет
- 9. Периодические изменения физической величины в зависимости от
- 10. Во всех трех случаях для синих кривых
- 11. Графики координаты x(t), скорости υ(t) и ускорения a(t) тела, совершающего гармонические колебания.
- 12. Закон сохранения энергии для пружинного маятника
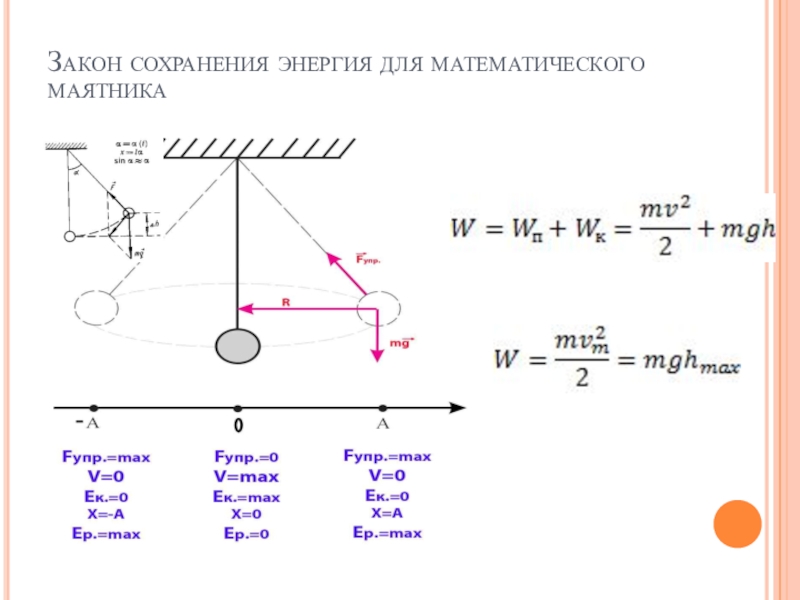
- 13. Закон сохранения энергия для математического маятника
- 14. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ.Затухающими наз. колебания, энергия (а значит,
- 15. Резонанс
Слайд 1Механические колебания
Автор: учитель физики МАОУ «Ждановская СОШ»
Трухов Александр Геннадьевич
Слайд 2Колебания - один из самых распространенных процессов в природе и технике
Механические
Колебания
Свободные вынужденные автоколебания
Слайд 3СВОБОДНЫЕ – колебания, возникающие в системе под действием внутренних сил
ВЫНУЖДЕННЫЕ–
АВТОКОЛЕБАНИЯ – незатухающие колебания, которые могут существовать в системе без воздействия на нее внешних периодических сил, за счет источника энергии (например, часы с маятником)
Слайд 4УСЛОВИЯ ВОЗНИКНОВЕНИЯ СВОБОДНЫХ КОЛЕБАНИЙ
при выведении тела из положения равновесия в
силы трения в системе должны быть достаточно малы.
Слайд 5Уравнение движение груза, подвешенного на пружине
- условие равновесия
- возвращающая сила
- собственная частота маятника
- уравнение движения маятника
Тело, подвешенное на пружине и совершающее колебания вдоль вертикальной оси под действием силы упругости пружины, называется пружинным маятником
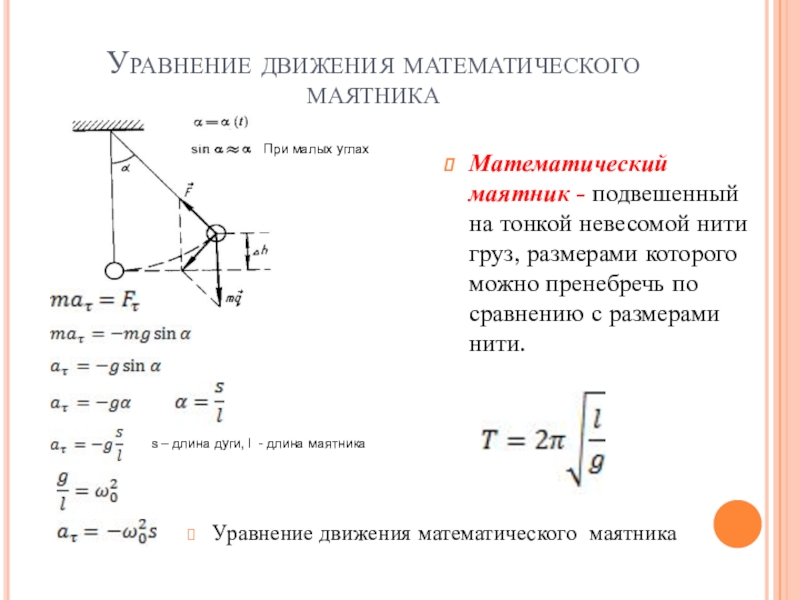
Слайд 6Уравнение движения математического маятника
Уравнение движения математического маятника
Математический маятник - подвешенный на
s – длина дуги, l - длина маятника
Слайд 7 xm – модуль максимального смещения точки от положения равновесия называется
Т – время одного полного колнбания называется периодом;
Т = t/n, где n – число полных колебаний
x – смещение точки от положения равновесия в данный момент времени.
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ
Слайд 8 φ – фаза колебаний, которая определяет состояние колебательной системы в
φ = ѡ0t + φ0 [φ] = рад
число колебаний в единицу времени называется частотой;
ѵ = 1/Т – линейная частота колебаний
ѵ = n/t [ѵ] = 1/c = 1 Гц (Герц)
Ѡ0 =2π/Т – циклическая частота колебаний
[ѡ0] = рад/с
Слайд 9Периодические изменения физической величины в зависимости от времени, происходящие по закону
x = xm sin(ω0 t + φ0)
уравнение гармонического колебания
Слайд 10
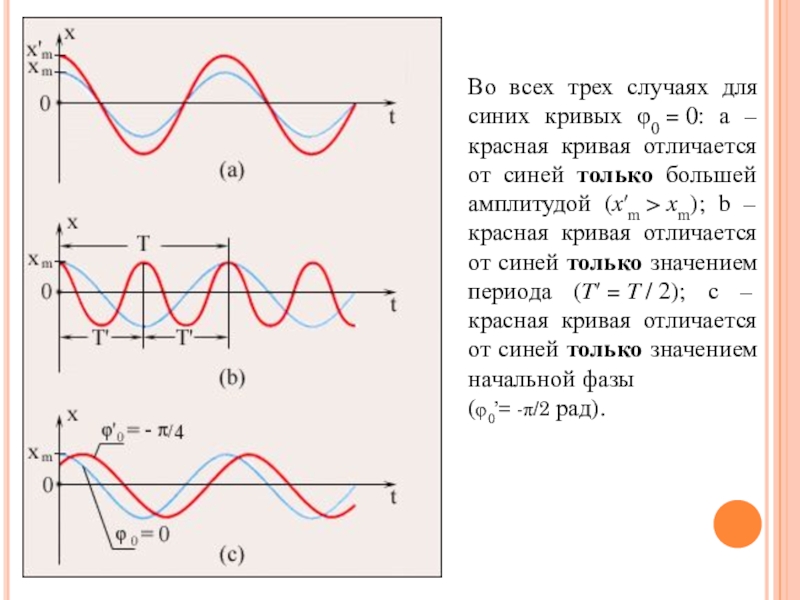
Во всех трех случаях для синих кривых φ0 = 0: а – красная
(φ0’= -π/2 рад).
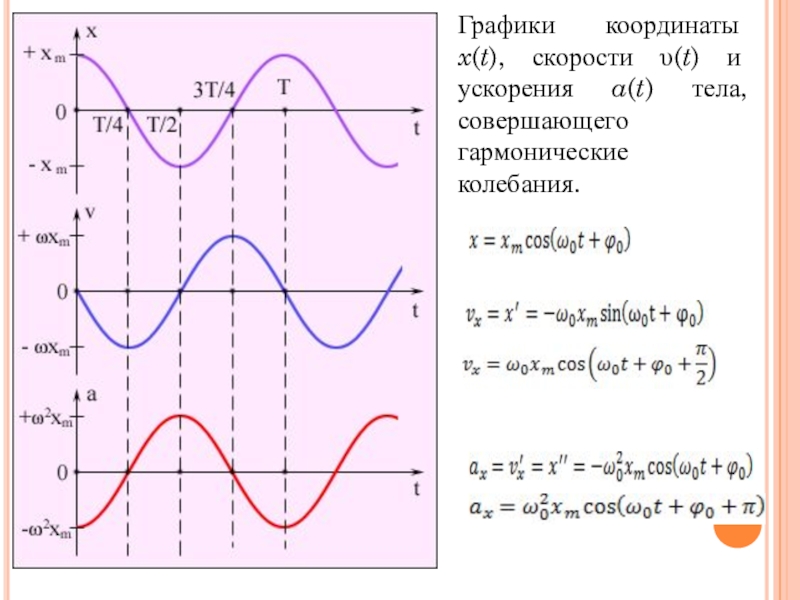
Слайд 11Графики координаты x(t), скорости υ(t) и ускорения a(t) тела, совершающего гармонические
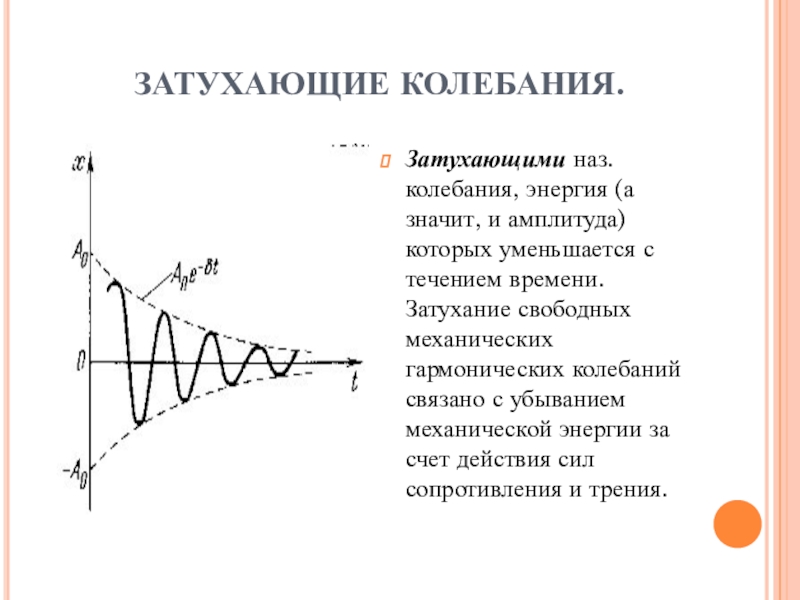
Слайд 14ЗАТУХАЮЩИЕ КОЛЕБАНИЯ.
Затухающими наз. колебания, энергия (а значит, и амплитуда) которых уменьшается
Слайд 15
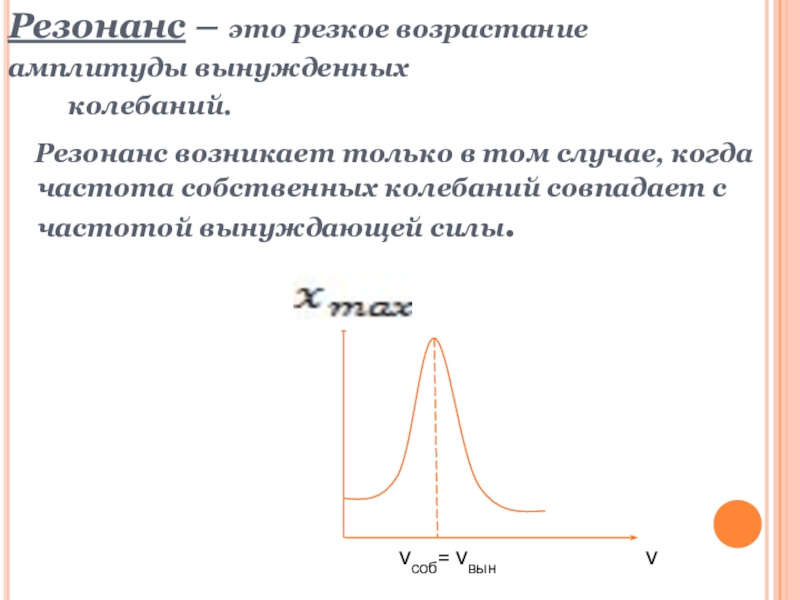
Резонанс – это резкое возрастание
амплитуды вынужденных
колебаний.
Резонанс возникает только в том случае, когда частота собственных колебаний совпадает с частотой вынуждающей силы.
соб= вын