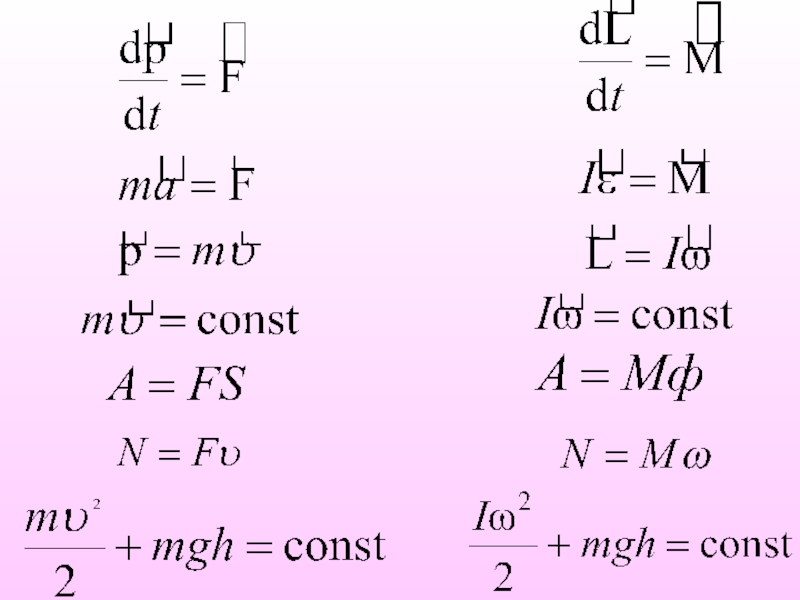точки.
2. Динамика вращательного движения твердого тела относительно оси.
3. Расчет моментов инерции некоторых простых тел. Теорема Штейнера.
4. Кинетическая энергия вращающегося тела.
5. Закон сохранения момента импульса.
6. Законы сохранения и их связь с симметрией пространства и времени.
7. Сходство и различие линейных и угловых характеристик движения.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по физике на тему Динамика вращательного движения твердого тела
Содержание
- 1. Презентация по физике на тему Динамика вращательного движения твердого тела
- 2. 1. Динамика вращательного движения твердого тела относительно
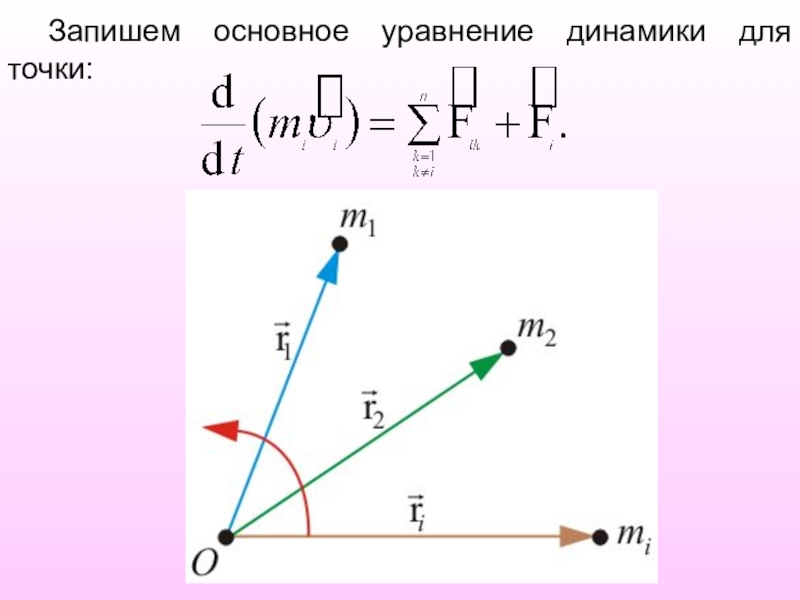
- 3. Запишем основное уравнение динамики для точки:
- 4. Умножим обе части векторно на Знак производной
- 5. Векторное произведение точки на
- 6. Векторное произведение проведенного в точку приложения
- 7. C учетом новых обозначений: Запишем систему n
- 8. Здесь сумма производных равна производной суммы:где
- 9. Основной закон динамики вращательного движения твердого тела,
- 10. Или L = [r,p]Здесь L − трехмерный момент импульса относительно центра вращения О.
- 11. 2. Динамика вращательного движения твердого тела относительно
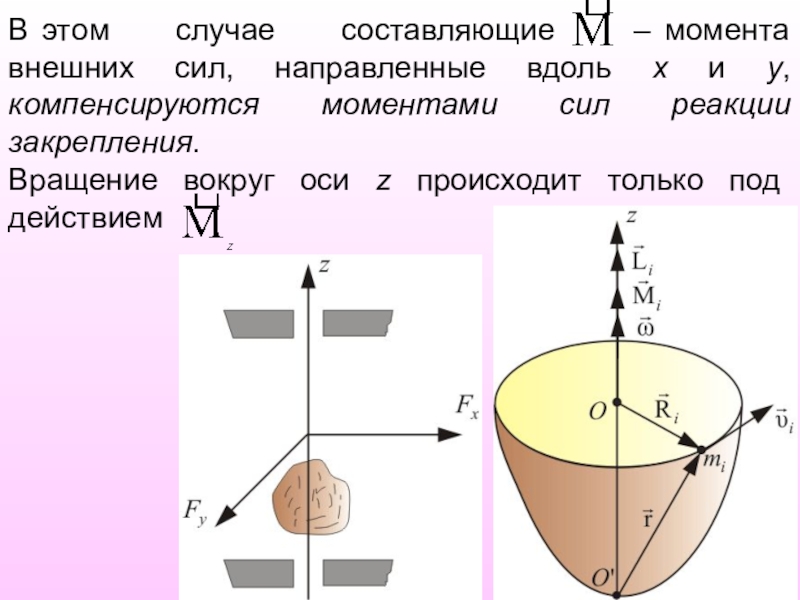
- 12. В этом случае
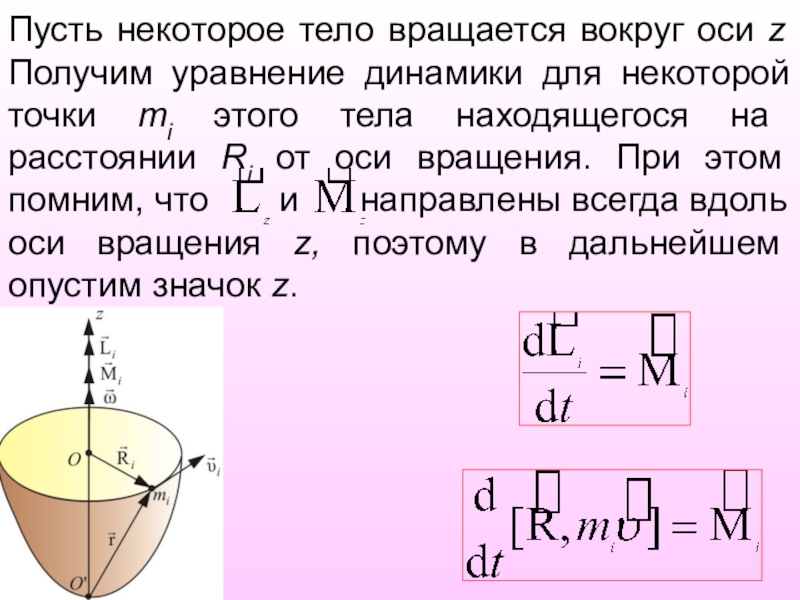
- 13. Пусть некоторое тело вращается вокруг оси z
- 14. Так как у всех
- 15. Обозначим Ii – момент инерции точки находящейся
- 16. Просуммировав по всем i-ым точкам, получим Это основное
- 17. где – момент импульса тела вращающегося
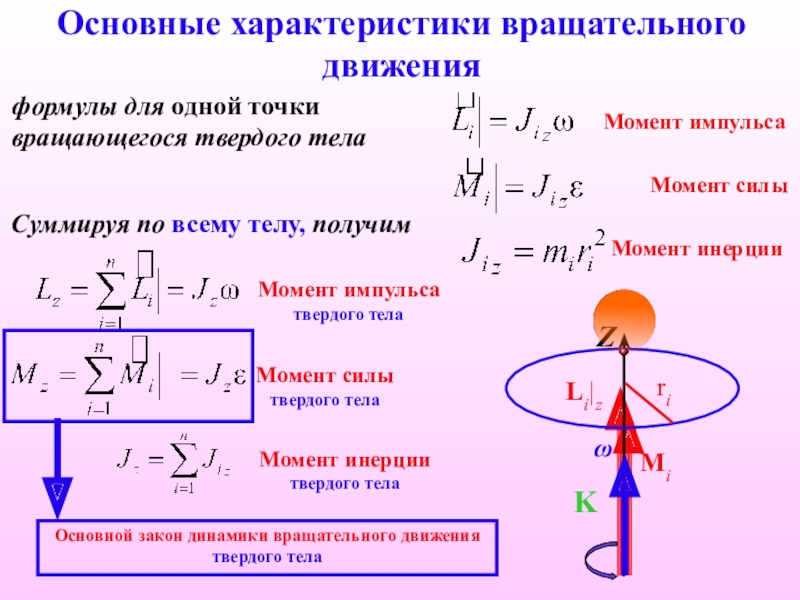
- 18. Основные характеристики вращательного движенияМомент импульсаформулы для одной
- 19. 3. Расчет моментов инерции некоторых простых тел.
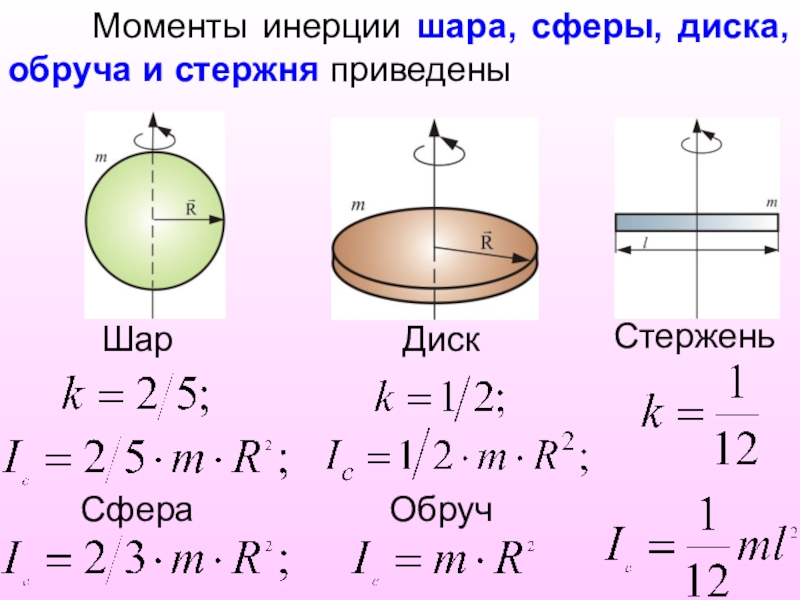
- 20. Моменты инерции шара, сферы, диска, обруча и стержня приведеныШарСфераДискОбручСтержень
- 21. При вычислении момента инерции тела, вращающегося вокруг
- 22. Момент инерции тела относительно любой оси вращения
- 23. Пример: стержень массой m, длиной l, вращается вокруг оси, проходящей через конец стержня.
- 24. 4. Кинетическая энергия вращающегося тела
- 25. Если тело вращается вокруг неподвижной оси z
- 26. В общем случае движение твердого тела можно
- 27. Пример:Скорость центра масс обруча равна v, масса
- 28. 5. Закон сохранения момента импульсаЗакон сохранения момента
- 29. Закон сохранения момента импульса – момент импульса
- 30. Если момент внешних сил относительно неподвижной оси
- 31. Используется гироскоп в различных навигационных устройствах кораблей,
- 32. Слайд 32
- 33. Слайд 33
- 34. 6. Законы сохранения и их связь
- 35. Импульс и момент импульса сохраняются в том
- 36. Равнозначность следует понимать в том смысле, что
- 37. 2. В основе закона сохранения импульса лежит
- 38. 3. В основе закона сохранения момента импульса
- 39. Если задана сила, действующая на материальную точку
- 40. Принципы запрета:Любое явление, при котором не выполняются
- 41. Может ли покоящееся тело за счет внутренней
- 42. При этом возникшие осколки могут двигаться так,
- 43. Фундаментальность законов сохранения заключается в их универсальности:
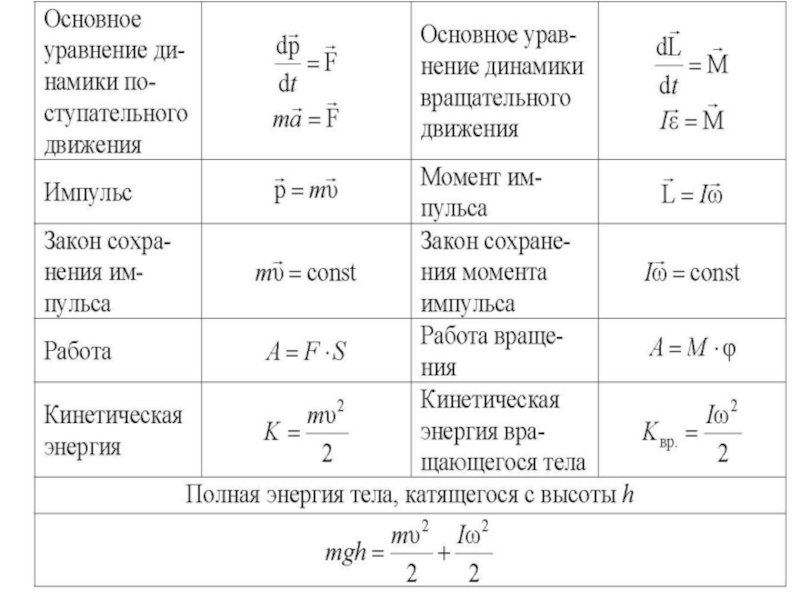
- 44. 7. Сходство и различие линейных и угловых
- 45. Поступательное движение Вращательное движение
- 46. Слайд 46
- 47. Слайд 47
- 48. Слайд 48
1. Динамика вращательного движения твердого тела относительно точкиРассмотрим твердое тело, как некую систему (рис.), состоящую из n точек (m1 m2 … mn); – радиус-вектор i-ой точки, проведенный из точки О – центра неподвижной
Слайд 1ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
1. Динамика вращательного движения твердого тела относительно
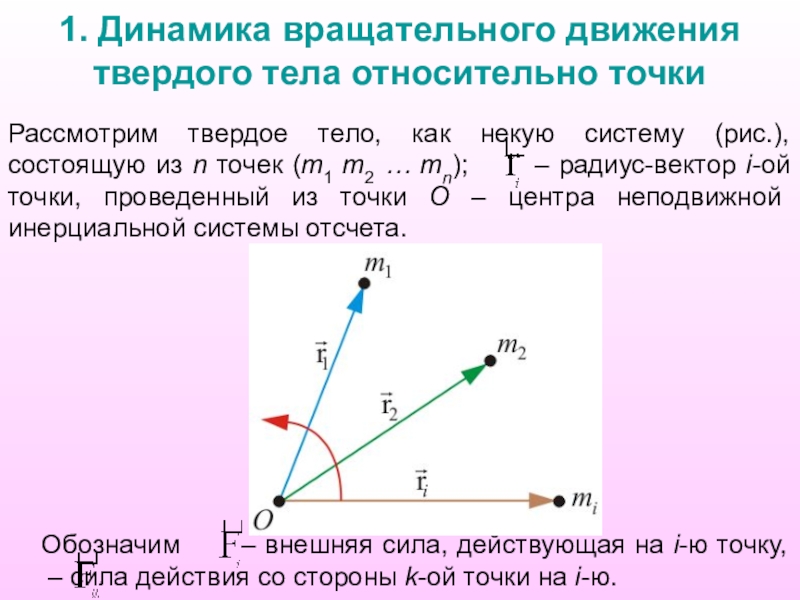
Слайд 21. Динамика вращательного движения твердого тела относительно точки
Рассмотрим твердое тело, как
некую систему (рис.), состоящую из n точек (m1 m2 … mn); – радиус-вектор i-ой точки, проведенный из точки О – центра неподвижной инерциальной системы отсчета.
Обозначим – внешняя сила, действующая на i-ю точку, – сила действия со стороны k-ой точки на i-ю.
Обозначим – внешняя сила, действующая на i-ю точку, – сила действия со стороны k-ой точки на i-ю.
Слайд 4Умножим обе части векторно на
Знак производной можно вынести за знак
векторного произведения (и знак суммы тоже), тогда:
Слайд 5 Векторное произведение точки на её импульс называется моментом
импульса этой точки относительно точки О.
Эти три вектора образуют правую тройку векторов, связанных «правилом буравчика»:
Слайд 6Векторное произведение проведенного в точку приложения сил, на эту силу
называется моментом силы
Обозначим li – плечо силы Fi, . Т.к.
то:
Слайд 7C учетом новых обозначений:
Запишем систему n уравнений для всех точек
системы и сложим, левые и правые части уравнений:
Так как
то
Слайд 8 Здесь сумма производных равна производной суммы:
где – момент
импульса системы,
– результирующий момент всех внешних сил относительно точки О.
Окончательно получим:
– результирующий момент всех внешних сил относительно точки О.
Окончательно получим:
Слайд 9Основной закон динамики вращательного движения твердого тела, вращающегося вокруг точки.
Момент импульса
системы является основной динамической характеристикой вращающегося тела.
Основное уравнение динамики поступательного движения
Основное уравнение динамики поступательного движения
![Или L = [r,p]Здесь L − трехмерный момент импульса относительно центра вращения О.](/img/thumbs/59a082d4fa2be708451976e85fdf24c4-800x.jpg "Презентация по физике на тему Динамика вращательного движения твердого тела Или L = [r,p]Здесь L − трехмерный момент импульса относительно центра вращения О.")
Слайд 112. Динамика вращательного движения твердого тела относительно оси
Вычислить вектор
– момент импульса системы относительно произвольной точки не просто: надо знать шесть проекций (три задают положение тела, три задают положение точки).
Значительно проще найти момент импульса тела, вращающегося вокруг неподвижной оси (z)
Значительно проще найти момент импульса тела, вращающегося вокруг неподвижной оси (z)
Слайд 12В этом случае составляющие –
момента внешних сил, направленные вдоль x и y, компенсируются моментами сил реакции закрепления.
Вращение вокруг оси z происходит только под действием
Вращение вокруг оси z происходит только под действием
Слайд 13Пусть некоторое тело вращается вокруг оси z Получим уравнение динамики для
некоторой точки mi этого тела находящегося на расстоянии Ri от оси вращения. При этом помним, что и направлены всегда вдоль оси вращения z, поэтому в дальнейшем опустим значок z.
Слайд 14Так как у всех точек разная, введем, вектор
угловой скорости , причем
Тогда
Так как тело абсолютно твердое, то в процессе вращения mi и Ri останутся неизменными. Тогда:
Слайд 15Обозначим Ii – момент инерции точки находящейся на расстоянии R от
оси вращения:
Так как тело состоит из огромного количества точек и все они находятся на разных расстояниях от оси вращения, то момент инерции тела равен:
где R – расстояние от оси z до dm.
Как видно, момент инерции I – величина скалярная.
Слайд 16Просуммировав по всем i-ым точкам, получим
Это основное уравнение динамики тела вращающегося
вокруг неподвижной оси.
Основное уравнение динамики поступательного движения тела.
Основное уравнение динамики поступательного движения тела.
Слайд 17
где – момент импульса тела вращающегося вокруг оси z
(для поступательного
движения ).
При этом помним, что и динамические характеристики вращательного движения направленные всегда вдоль оси вращения..
При этом помним, что и динамические характеристики вращательного движения направленные всегда вдоль оси вращения..
Слайд 18Основные характеристики вращательного движения
Момент импульса
формулы для одной точки вращающегося твердого тела
Суммируя
по всему телу, получим
Момент силы
Li|z
Mi
Момент инерции
Момент импульса твердого тела
Момент силы твердого тела
Момент инерции твердого тела
Основной закон динамики вращательного движения твердого тела
Z
K
ω
ri
Слайд 21При вычислении момента инерции тела, вращающегося вокруг оси, не проходящей через
центр инерции, следует пользоваться теоремой о параллельном переносе осей или теоремой Штейнера (Якоб Штейнер, швейцарский геометр 1796 – 1863 гг.).
Теорема Штейнера
Слайд 22
Момент инерции тела относительно любой оси вращения равен моменту его инерции
относительно параллельной оси, проходящей через центр масс С тела, плюс произведение массы тела на квадрат расстояния между осями.
Теорема Штейнера
Слайд 25 Если тело вращается вокруг неподвижной оси z с угловой скоростью
то линейная скорость i-й точки
Следовательно,
Следовательно,
Момент инерции тела I – является мерой инертности при вращательном движении. Так же как масса m – мера инерции при поступательном движении.
Слайд 26 В общем случае движение твердого тела можно представить в виде суммы
двух движений – поступательного со скоростью и вращательного с угловой скоростью вокруг мгновенной оси, проходящей через центр инерции. Полная кинетическая энергия этого тела:
Здесь Ic – момент инерции относительно мгновенной оси вращения, проходящей через центр инерции.
Слайд 27Пример:Скорость центра масс обруча равна v, масса обруча m. Определим его
кинетическую энергию при движении по горизонтальной поверхности.
Имеем
Kполн = + ,
– линейная скорость обода.
Для наблюдателя,
движущегося вместе с центром
обруча, скорость точки
соприкосновения обруча с плоскостью
равна v. Поэтому = v.
Таким образом, Kполн = + = mv2.
Имеем
Kполн = + ,
– линейная скорость обода.
Для наблюдателя,
движущегося вместе с центром
обруча, скорость точки
соприкосновения обруча с плоскостью
равна v. Поэтому = v.
Таким образом, Kполн = + = mv2.
Слайд 285. Закон сохранения момента импульса
Закон сохранения момента импульса
Для замкнутой системы тел
момент внешних сил всегда равен нулю, так как внешние силы вообще не действуют на замкнутую систему:
Слайд 29 Закон сохранения момента импульса – момент импульса замкнутой системы тел относительно
любой неподвижной точки не изменяется с течением времени.
Это один из фундаментальных законов природы.
Аналогично для замкнутой системы вращающихся вокруг оси z:
Это один из фундаментальных законов природы.
Аналогично для замкнутой системы вращающихся вокруг оси z:
отсюда
или
Слайд 30 Если момент внешних сил относительно неподвижной оси вращения тождественно равен нулю,
то момент импульса относительно этой оси не изменяется в процессе движения.
Момент импульса и для незамкнутых систем постоянен, если результирующий момент внешних сил, приложенных к системе, равен нулю.
Момент импульса и для незамкнутых систем постоянен, если результирующий момент внешних сил, приложенных к системе, равен нулю.
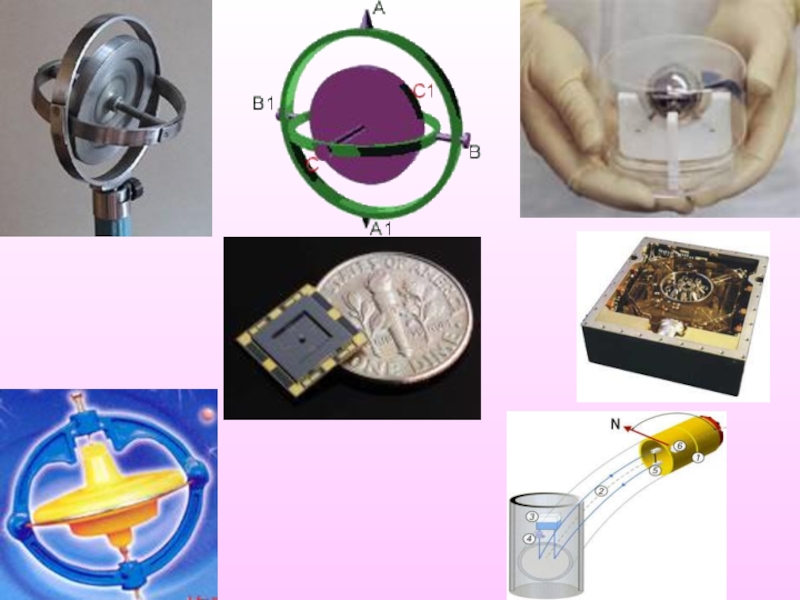
Слайд 31 Используется гироскоп в различных навигационных устройствах кораблей, самолетов, ракет (гирокомпас, гирогоризонт).
Уравновешенный гироскоп – быстро вращающееся тело, имеющее три степени свободы
Слайд 34
6. Законы сохранения и их связь с симметрией
пространства и времени
Законы сохранения
есть следствие симметрии пространства – времени.
Три фундаментальных закона природы:
закон сохранения импульса,
момента импульса,
энергии.
Эти законы выполняются только в инерциальных системах отсчета.
Три фундаментальных закона природы:
закон сохранения импульса,
момента импульса,
энергии.
Эти законы выполняются только в инерциальных системах отсчета.
Слайд 35 Импульс и момент импульса сохраняются в том случае, если систему можно
считать замкнутой (сумма всех внешних сил и всех моментов сил равна нулю).
Для сохранения энергии тела условия замкнутости недостаточно – тело должно быть еще и адиабатически изолированным (т.е. не участвовать в теплообмене).
Для сохранения энергии тела условия замкнутости недостаточно – тело должно быть еще и адиабатически изолированным (т.е. не участвовать в теплообмене).
Слайд 36Равнозначность следует понимать в том смысле, что замена моментом времени t1
на момент времени t2, без изменения значений координат и скорости частиц не изменяет механические свойства системы.
1. В основе закона сохранения энергии лежит однородность времени, т. е. равнозначность всех моментов времени (симметрия по отношению к сдвигу начала отсчета времени).
Слайд 372. В основе закона сохранения импульса лежит однородность пространства, т. е.
одинаковость свойств пространства во всех точках (симметрия по отношению к сдвигу начала координат).
Одинаковость следует понимать в том смысле, что параллельный перенос замкнутой системы из одного места пространства в другое, без изменения взаимного расположения и скоростей частиц, не изменяет механические свойства системы.
Одинаковость следует понимать в том смысле, что параллельный перенос замкнутой системы из одного места пространства в другое, без изменения взаимного расположения и скоростей частиц, не изменяет механические свойства системы.
Слайд 38 3. В основе закона сохранения момента импульса лежит изотропия пространства, т.
е. одинаковость свойств пространства по всем направлениям (симметрия по отношению к повороту осей координат).
Одинаковость следует понимать в том смысле, что поворот замкнутой системы, как целого, не отражается на её механических свойствах.
Одинаковость следует понимать в том смысле, что поворот замкнутой системы, как целого, не отражается на её механических свойствах.
Слайд 39Если задана сила, действующая на материальную точку и начальные условия, то
можно найти закон движения, траекторию, величину и направление скорости в любой момент времени и т. п.
Законы сохранения не дают нам прямых указаний на то, как должен идти тот или иной процесс. Они говорят лишь о том, какие процессы запрещены и потому в природе не происходят.
Законы сохранения не дают нам прямых указаний на то, как должен идти тот или иной процесс. Они говорят лишь о том, какие процессы запрещены и потому в природе не происходят.
Между законами и законами сохранения имеется принципиальная разница.
Слайд 40 Принципы запрета:
Любое явление, при котором не выполняются хотя бы один из
законов сохранения, запрещено, и в природе такие явления никогда не наблюдаются.
Всякое явление, при котором не нарушается ни один из законов сохранения, в принципе может происходить.
Всякое явление, при котором не нарушается ни один из законов сохранения, в принципе может происходить.
Слайд 41Может ли покоящееся тело за счет внутренней энергии начать двигаться? Этот
процесс не противоречит закону сохранения энергии. Нужно лишь, чтобы возникающая кинетическая энергия точно равнялась убыли внутренней энергии.
Такой процесс противоречит закону сохранения импульса. Раз тело покоилось, то его импульс был равен нулю. А если оно станет двигаться, то его импульс сам собой увеличится, что невозможно. Поэтому внутренняя энергия тела не может превратиться в кинетическую, если тело не распадётся на части.
Такой процесс противоречит закону сохранения импульса. Раз тело покоилось, то его импульс был равен нулю. А если оно станет двигаться, то его импульс сам собой увеличится, что невозможно. Поэтому внутренняя энергия тела не может превратиться в кинетическую, если тело не распадётся на части.
Слайд 42 При этом возникшие осколки могут двигаться так, чтобы их центр масс
оставался в покое, – а только этого и требует закон сохранения импульса.
Итак, для того чтобы внутренняя энергия покоящегося тела могла превратиться в кинетическую, это тело должно распадаться на части. Если же есть еще один какой-либо закон, запрещающий распад этого тела на части, то его внутренняя энергия и масса покоя будут постоянными величинами.
Итак, для того чтобы внутренняя энергия покоящегося тела могла превратиться в кинетическую, это тело должно распадаться на части. Если же есть еще один какой-либо закон, запрещающий распад этого тела на части, то его внутренняя энергия и масса покоя будут постоянными величинами.
Слайд 43Фундаментальность законов сохранения заключается в их универсальности:
- Они справедливы при
изучении любых физических процессов (механических, тепловых, электромагнитных, и др.).
- Они одинаково применимы в релятивистском и нерелятивистском движении,
в микромире, где справедливы квантовые представления
в макромире.
- Они одинаково применимы в релятивистском и нерелятивистском движении,
в микромире, где справедливы квантовые представления
в макромире.
Слайд 447. Сходство и различие линейных и угловых
характеристик движения
Формулы кинематики и динамики
вращательного движения легко запоминаются, если сопоставить их с формулами поступательного движения
