- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по физике Газовые законы
Содержание
- 1. Презентация по физике Газовые законы
- 2. Особенности газов. Виды газовСреди всех агрегатных состояний
- 3. Описание газов в физике Поскольку изучаемое
- 4. Кем и когда были открыты газовые законыЗакон
- 5. Закон Бойля-Мариотта (изотермический процесс)Изотермическим процессом называют изменение состояния
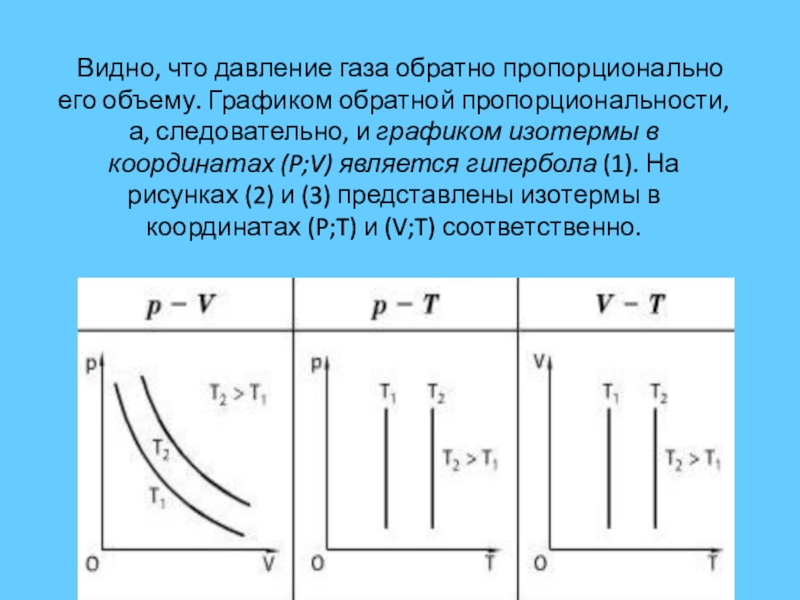
- 6. Видно, что давление газа обратно пропорционально
- 7. Закон Гей-Люссака (изобарный процесс) Изобарным процессом
- 8. Рассмотрим два изобарных процесса с
- 9. Закон Шарля (изохорный процесс)Изохорным процессом называют изменение
- 10. Рассмотрим два изохорных процесса с
- 11. Из всего выше сказанного, по поводу этих
- 12. Газовый закон Менделеева-Клапейрона Этот закон объединяет
- 13. Примеры решения задачЗадача 1 Задача: До
- 14. Задача 3 Задание: В кислородной системе,
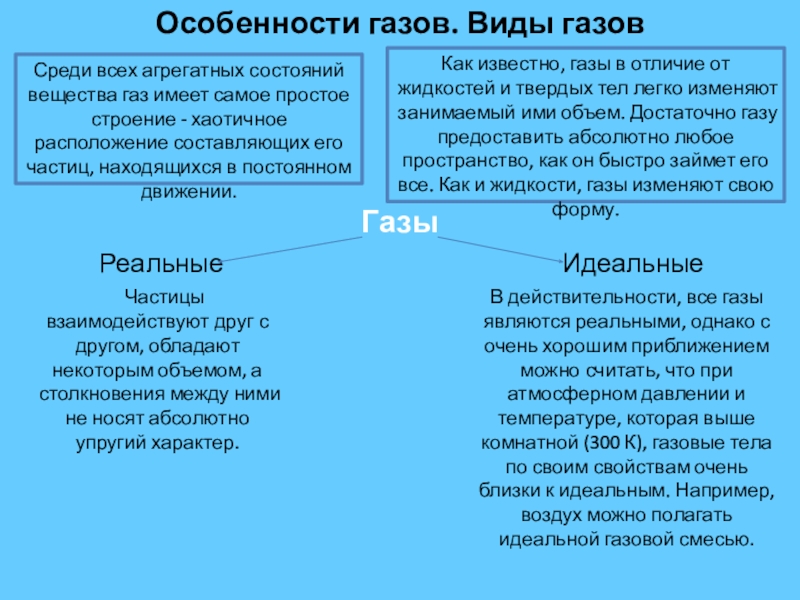
Слайд 2Особенности газов. Виды газов
Среди всех агрегатных состояний вещества газ имеет самое
Как известно, газы в отличие от жидкостей и твердых тел легко изменяют занимаемый ими объем. Достаточно газу предоставить абсолютно любое пространство, как он быстро займет его все. Как и жидкости, газы изменяют свою форму.
Газы
Реальные
Идеальные
Частицы взаимодействуют друг с другом, обладают некоторым объемом, а столкновения между ними не носят абсолютно упругий характер.
В действительности, все газы являются реальными, однако с очень хорошим приближением можно считать, что при атмосферном давлении и температуре, которая выше комнатной (300 К), газовые тела по своим свойствам очень близки к идеальным. Например, воздух можно полагать идеальной газовой смесью.
Слайд 3Описание газов в физике
Поскольку изучаемое агрегатное состояние вещества не
Важными термодинамическими макроскопическими характеристиками являются следующие:
Температура - мера энергии кинетической молекул и атомов газа. Измеряется в Кельвинах (К).
Давление - мера количества движения, которое передает стенкам сосуда частица при столкновении с ними. Эта величина зависит от температуры и числа частиц в заданном объеме. Измеряется оно в Паскалях (Па).
Объем - геометрическая макроскопическая характеристика, отражающая часть пространства, занимаемую газом. Измеряется в кубических метрах (м3).
Существует еще один параметр - это количество вещества. Оно отражает число частиц, которое содержит 1 грамм атомарного водорода или 2 грамма молекулярного водорода H2. Измеряется количество вещества в молях. Один моль равен числу Авогадро (NA = 6,02*1023).
Газовые законы – это законы, описывающие изопроцессы в идеальном газе.
Процессы, при которых один из параметров состояния газа остается постоянным называют изопроцессами.
Слайд 4Кем и когда были открыты газовые законы
Закон Бойля-Мариотта (изотермический процесс) был экспериментально
Роберт Бойль (1) / Эдм Мариотт (2)
Закон Гей-Люссака (изобарный процесс) был впервые опубликован в 1802 году химиком и физиком Жозефом Луи Гей-Люссаком
Закон Шарля или второй закон Гей-Люссака (изохорный процесс) был установлен в 1787 году Шарлем и уточнен Гей-Люссаком в 1802 году
Жак Шарль (3) / Жозеф Луи Гей-Люссак (4)
Слайд 5Закон Бойля-Мариотта (изотермический процесс)
Изотермическим процессом называют изменение состояния газа, при котором его
Для неизменной массы газа при постоянной температуре произведение давления газа на объем есть величина постоянная:
Этот же закон можно переписать в другом виде (для двух состояний идеального газа)
Этот закон следует из уравнения Менделеева – Клапейрона:
Очевидно, что при неизменной массе газа и при постоянной температуре правая часть уравнения остается постоянной величиной.
Графики зависимости параметров газа при постоянной температуре называются изотермами.
Обозначив константу буквой K1, запишем функциональную зависимость давления от объема при изотермическом процессе:
p = k1/V
Слайд 6 Видно, что давление газа обратно пропорционально его объему. Графиком обратной
Слайд 7Закон Гей-Люссака (изобарный процесс)
Изобарным процессом называют изменение состояния газа,
Для неизменной массы газа при постоянном давлении отношение объема газа к температуре есть величина постоянная:
V/T=const
Для двух состояний газа этот закон запишется в виде:
V1/T1=V2/T2
Этот закон также следует из уравнения Менделеева – Клапейрона:
V/T=const=mR/@*1/p
@-ню
Графики зависимости параметров газа при постоянном давлении называются изобарами.
Слайд 8 Рассмотрим два изобарных процесса с давлениями p1 и p2
Определим вид графика в координатах (V,T). Обозначив константу буквой k2, запишем функциональную зависимость объема от температуры при изобарном процессе:
V=k2*T
Видно, что при постоянном давлении объем газа прямо пропорционален его температуре. Графиком прямой пропорциональности, а, следовательно, и графиком изобары в координатах (V,T) является прямая, проходящая через начало координат (3). В реальности при достаточно низких температурах все газы превращаются в жидкости, к которым газовые законы уже неприменимы. Поэтому вблизи начала координат изобары (3) показаны пунктиром.
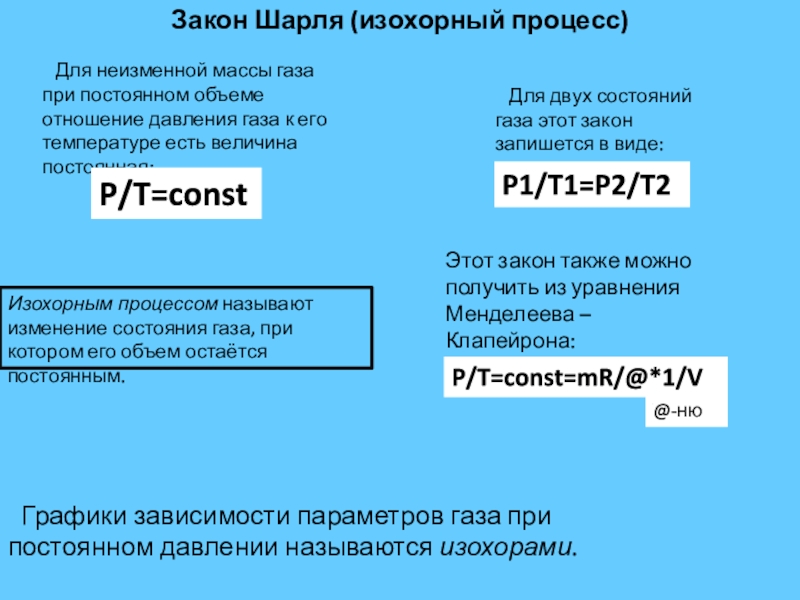
Слайд 9Закон Шарля (изохорный процесс)
Изохорным процессом называют изменение состояния газа, при котором
Для неизменной массы газа при постоянном объеме отношение давления газа к его температуре есть величина постоянная:
P/T=const
Для двух состояний газа этот закон запишется в виде:
P1/T1=P2/T2
Этот закон также можно получить из уравнения Менделеева – Клапейрона:
P/T=const=mR/@*1/V
@-ню
Графики зависимости параметров газа при постоянном давлении называются изохорами.
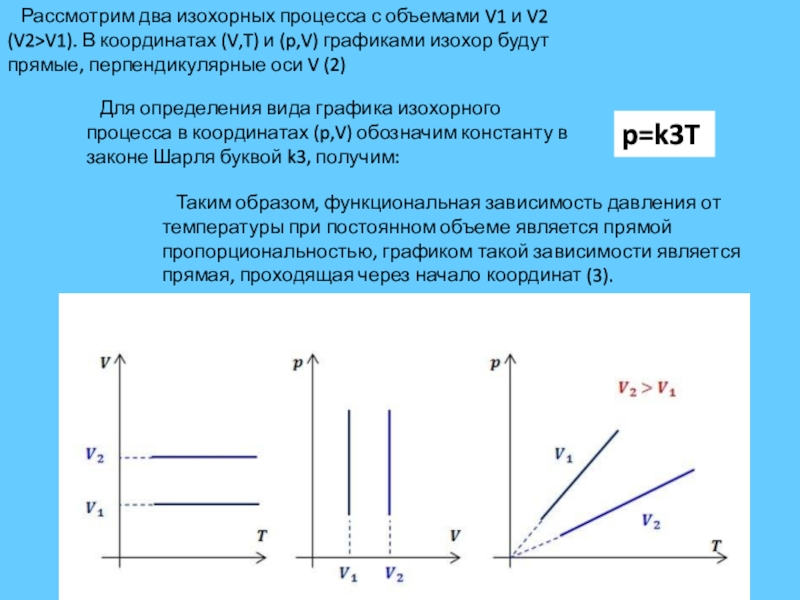
Слайд 10 Рассмотрим два изохорных процесса с объемами V1 и V2 (V2>V1).
Для определения вида графика изохорного процесса в координатах (p,V) обозначим константу в законе Шарля буквой k3, получим:
p=k3T
Таким образом, функциональная зависимость давления от температуры при постоянном объеме является прямой пропорциональностью, графиком такой зависимости является прямая, проходящая через начало координат (3).
Слайд 11Из всего выше сказанного, по поводу этих трёх законов, можно привести
Нагреем газ в закрытом сосуде. Ясно, что атомы или молекулы начнут двигаться быстрее, а значит, с большей силой случать в стенки. Вывод: при постоянном объеме газа его давление пропорционально температуре (закон Шарля).
Если газ нагревать и дать возможность расширяться (как в воздушном шарике), то будет расти уже его объем. Следовательно, при постоянном давлении объем газа пропорционален его температуре (закон Гей-Люссака).
Если сжать газ (уменьшить объем), сохраняя его температуру, молекулы в меньшем объеме будут быстрее преодолевать расстояние между стенками и чаще ударяться о них. Больше ударов — больше давление. Отсюда следует, что давление газа при постоянной температуре обратно пропорционально его объему (закон Бойля—Мариотта).
V/T=const
P/T=const
Слайд 12Газовый закон Менделеева-Клапейрона
Этот закон объединяет все изложенные и описанные
P*V = n*R*T
Видно, что это выражение объединяет все четыре макроскопических параметра (n, P, V, T), которые фигурируют в описанных ранее газовых законах. Универсальная газовая постоянная R - это величина, которая показывает значение работы, выполняемой 1 моль идеальным газом во время его расширения при нагреве на 1 К. Она равна 8,314 Дж/(моль*К).
Нетрудно догадаться, что полагая константой ту или иную величину, можно получить все предыдущие формулы для идеального газа.
Уравнение состояния было получено в первой половине XIX века французским физиком и инженером Эмилем Клапейроном, поэтому оно часто носит только его фамилию. Однако сам Клапейрон, анализируя экспериментальные данные, сформулировал это уравнение с использованием нескольких констант. Впоследствии русский химик Дмитрий Менделеев ввел понятие универсальной газовой постоянной, выразив ее через другие известные константы:
R = Na*kb
Где kb - это постоянная Больцмана (1,38*10^-23 Дж/К)
P*V = N*kb*T
Где N - количество частиц
Слайд 13Примеры решения задач
Задача 1
Задача: До какой температуры нужно изобарически
Решение: Изобарный процесс (p=const) описывается законом Гей-Люссака (V1/T1=V2/T2).
По условию задачи объем газа вследствие изобарного охлаждения уменьшается на одну четверть, V2=0,75V1
Тогда V2=0,75V1 V1/T1=0,75V1/T2
Откуда конечная температура газа T2=0,75T1
Переведем единицы в систему СИ: начальная температура газа T1=37C’=310K
Вычислим T2=0,75*310=233K
Ответ: Газ нужно охладить до температуры 233К
K=C’+273’
Задача 2
Задание: В закрытом сосуде находится газ под давлением 200 кПа. Каким станет давление газа, если температуру повысить на 30%?
Решение: Так как сосуд с газом закрытый, объем газа не меняется. Изохорный процесс описывается законом Шарля (p1/T1=p2/T2)
По условию задачи температура газа повысилась на 30%, поэтому можно записать T2=T1+0,3T1=1,3T1
Подставив последнее соотношение в закон Шарля, получим p1/T1=p2/1,3T2
Откуда p2=1,3p1
Переведем единицы в систему СИ: начальное давление газа p1=200кПа=2*10^5Па
Вычислим: p2=1,3*2*10^5=2,6*10^5Pa=260kPf
Ответ: Давление газа станет равным 260 кПа
Слайд 14Задача 3
Задание: В кислородной системе, которой оборудован самолет, имеется
Решение: Изотермический процесс (T=const) описывается законом Бойля-Мариотта (p1V1=p2(V1+V2))
Откуда давление, установившееся в системе p2=p1V1/V1+V2
Вычислим p2=2*10^7*2,8*10^-3/2,8*10^-3+5*10^-2=7,2*10^6 Pa
Ответ: В системе установится давление 7,2*10^6 Pa
Задача 4
Задача: Водород массой 0,5 кг закачали в баллон объемом 100 литров при температуре 300 К. Необходимо определить давление в баллоне, которое будет создавать газ.
Решение: Прежде чем воспользоваться универсальным уравнением, следует привести все единицы измерения к СИ V = 100 л = 0,1 м^3
Количество вещества n газа можно определить по следующей формуле n = m/M(H2) = 500 г/(2 г/моль) = 250 моль
Здесь MH2 - молярная масса молекулярного водорода
Теперь можно воспользоваться универсальным уравнением: P*V = n*R*T
P = n*R*T/V = 250*8,314*300/0,1 = 6235500 Па
Полученное давление соответствует значению 61,5 атмосферы. При таком давлении некоторые приближения идеального газа могут не выполняться.