- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Первый признак подобия треугольников
Содержание
- 1. Презентация Первый признак подобия треугольников
- 2. Повторение изученного № 549Дано:
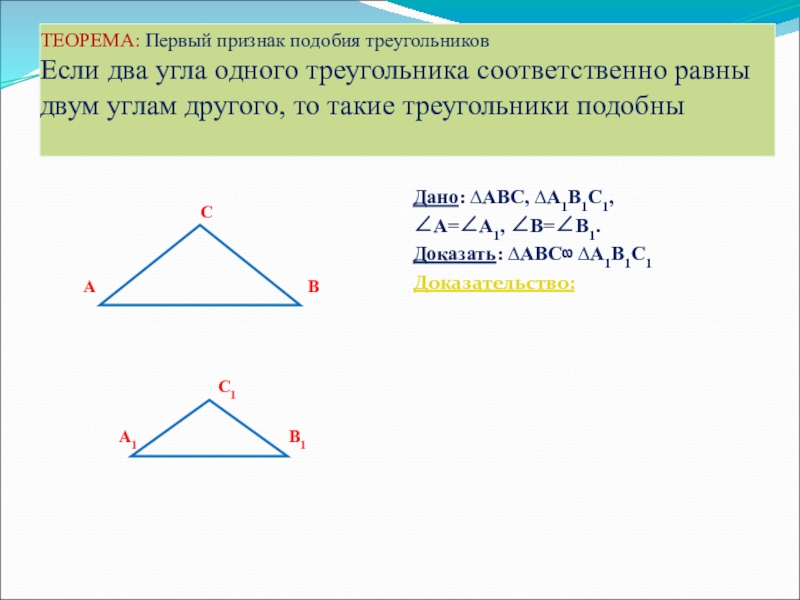
- 3. ТЕОРЕМА: Первый признак подобия треугольников Если два
- 4. Дано: ∆ABC, ∆A1B1C1, ∠A=∠A1, ∠B=∠B1.Доказать: ∆ABC∾ ∆A1B1C1Доказательство:1.Так
- 5. Закрепление № 550а)
- 6. Закрепление № 551(а)Дано: ABCD – параллелограмм,
- 7. Постановка домашнего задания Глава VII: §1, §2
- 8. Взаимопроверка домашнего задания по образцу № 551
- 9. Взаимопроверка домашнего задания по образцу №
- 10. Взаимопроверка домашнего задания по образцу №
Слайд 1Первый признак подобия треугольников
ГЕОМЕТРИЯ - 8
Ионашку Ирина Владимировна
МКОУ Кайгородская ООШ
Слайд 2
Повторение изученного № 549
Дано: ∆ABC ∾ ∆A1B1C1, BC
Найти: A1B1, B1C1, A1C1
Решение:
1.PABC = AB + BC + AC = 65 (см)
2.
3.
4.
5.
Ответ: A1B1=12см, B1C1=6см, A1C1=8см.
C
20 15
A 30 B
C1
A1 B1
Слайд 3ТЕОРЕМА: Первый признак подобия треугольников Если два угла одного треугольника соответственно равны
Дано: ∆ABC, ∆A1B1C1,
∠A=∠A1, ∠B=∠B1.
Доказать: ∆ABC∾ ∆A1B1C1
Доказательство:
C
A B
C1
A1 B1
Слайд 4Дано: ∆ABC, ∆A1B1C1, ∠A=∠A1, ∠B=∠B1.
Доказать: ∆ABC∾ ∆A1B1C1
Доказательство:
1.Так как по условию ∠A=∠A1,
2.Используем т. «Об отношении площадей ∆-ов, имеющих по равному углу, докажем, что стороны ∆ABC пропорциональны сходственным сторонам ∆A1B1C1:
3.Аналогично рассуждая и используя равенство углов ∠A=∠A1, ∠B=∠B1,
получим
4.Итак углы треугольников соответственно равны, их сходственные стороны пропорциональны, значит по определению подобных треугольников ∆ABC∾ ∆A1B1C1.
Что и требовалось доказать.
Слайд 5
Закрепление № 550
а) так как два угла
б) треугольники подобны по двум углам.
Найду неизвестный катет меньшего треугольника по теореме Пифагора:
Получаем:
Ответ: а) 9, б) 21
а) ?
8 х
?
12 6
б)
у 10
20 8
Слайд 6
Закрепление № 551(а)
Дано: ABCD – параллелограмм, E Є CD,
AE
Найти: EF, FC
Решение:
1.Так как ∠FEC=∠DEA – как вертикальные,
∠FCE=∠EDA – как накрест лежащие,
то ∆CEF∾ ∆ADE (по двум углам)
2.Значит
3.По свойству параллелограмма BC=AD=7см, отсюда:
Ответ: EF = 5см, FC = 3,5см.
F
C 4 E 8 D
7 10
B A
Слайд 7Постановка домашнего задания Глава VII: §1, §2 (п.59), вопросы 1-5, стр.160, теоремы с
Слайд 8
Взаимопроверка домашнего задания по образцу
№ 551 (б)
Дано: ABCD – параллелограмм, E
AE пересекает BC в точке F, AB=8см, AD=5см, CF=2см.
Найти: DE, CE
Решение:
1.Так как ∠FEC=∠DEA – как вертикальные,
∠FCE=∠EDA – как накрест лежащие,
то ∆CEF∾ ∆ADE (по двум углам)
2.Значит , AB=CD=8см.
Пусть CE=х, тогда DE=8-х.
3.Составлю пропорцию:
тогда
Ответ:
F
C E D
B A
Слайд 9
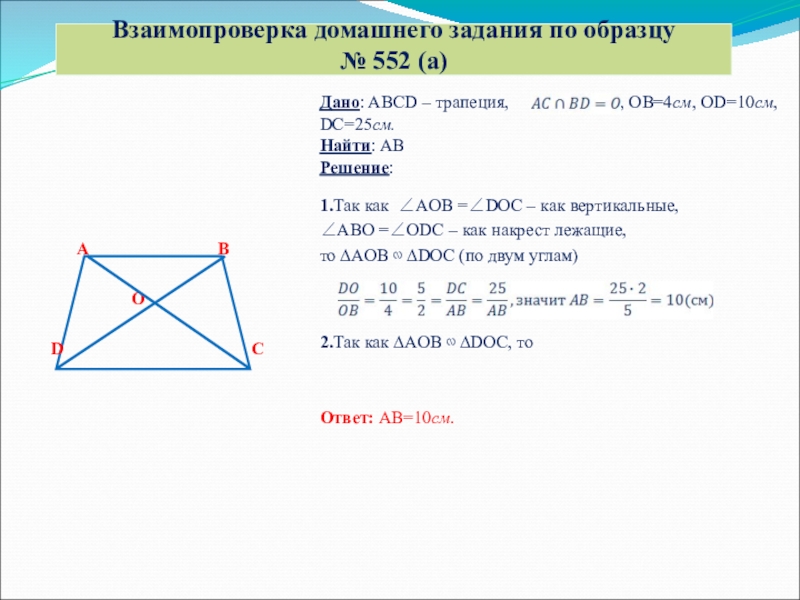
Взаимопроверка домашнего задания по образцу
№ 552 (а)
Дано: ABCD – трапеция,
Найти: AB
Решение:
1.Так как ∠AOB =∠DOC – как вертикальные,
∠ABO =∠ODC – как накрест лежащие,
то ∆AOB ∾ ∆DOC (по двум углам)
2.Так как ∆AOB ∾ ∆DOC, то
Ответ: AB=10см.
A B
O
D C
Слайд 10
Взаимопроверка домашнего задания по образцу
№ 554
Дано: ABCD – трапеция,
AB
Найти: BM, MC
Решение:
1.Так как ∠M – общий для ∆AMD и ∆BMC , ∠DAB =∠CBM
(как соответственные углы при параллельных CB и DA и секущей AM), то ∆AMD ∾ ∆BMC (по двум углам).
2.Так как ∆AMD ∾ ∆BMC то
3.Пусть BM = х, AM = 36+х
4. , x=6см
Значит BM=6см.
5.Пусть MC=y, тогда MD=y+3,9
Значит MC=6,5см.
Ответ: BM=6см, MC=6,5см
M
B 5 C
3,6 3,9
A 8 D