- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Открытый урок Применение производнойПлан урока
Содержание
- 1. Открытый урок Применение производнойПлан урока
- 2. Применение производной в физике, технике.11классНьютон Исаак(1643 – 1727) – английский физик и математик
- 3. Применение производной в физике, технике.11классНьютон Исаак(1643 – 1727) – английский физик и математик
- 4. Во всем мне хочется дойти до самой
- 5. Что называется
- 6. Что называется дифференциалом
- 7. Слайд 7
- 8. Слайд 8
- 9. Физический смысл производной.Скорость есть
- 10. Геометрический смысл
- 11. Слайд 11
- 12. Кроссворд По вертикали:1.Создатель дифференциального исчисления, использовавший понятие бесконечно
- 13. Ответы на вопросы кроссворда
- 14. Домашнее задание.Стр.137 рис.100, пример 7, разобрать, записать
- 15. Найти скорость и ускорение для точки,
- 16. Решение теста
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
Слайд 1Применение производной в физике, технике.
11класс
Ньютон Исаак
(1643 – 1727) –
английский физик
Слайд 2Применение производной в физике, технике.
11класс
Ньютон Исаак
(1643 – 1727) –
английский физик
Слайд 3Применение производной в физике, технике.
11класс
Ньютон Исаак
(1643 – 1727) –
английский физик
Слайд 4Во всем мне хочется дойти до самой сути… Эти слова Б.Л. Пастернака
Различные задачи естествознания – такие, как определение скорости, ускорения, силы тока, плотности вещества и многие другие – приводят к одним и тем же математическим вычислениям. Отвлекаясь от конкретного содержания каждой задачи, результат соответствующих математических вычислений называют производной.
Лейбниц Готфрид Фридрих
(1646 – 1716) – великий немецкий учёный. Философ, математик, физик, юрист, языковед. Создатель (наряду с Ньютоном) математического анализа.
Слайд 5Что называется
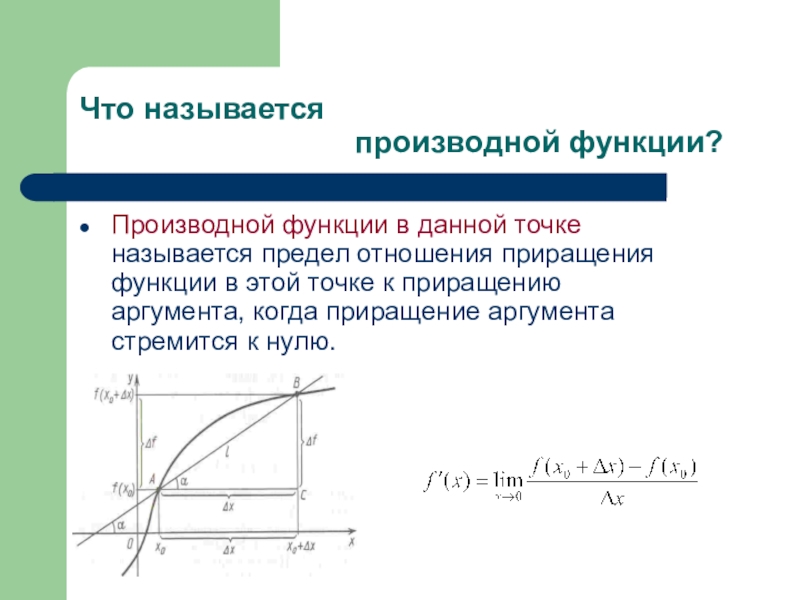
Производной функции в данной точке называется предел отношения приращения функции в этой точке к приращению аргумента, когда приращение аргумента стремится к нулю.
Слайд 6 Что называется дифференциалом
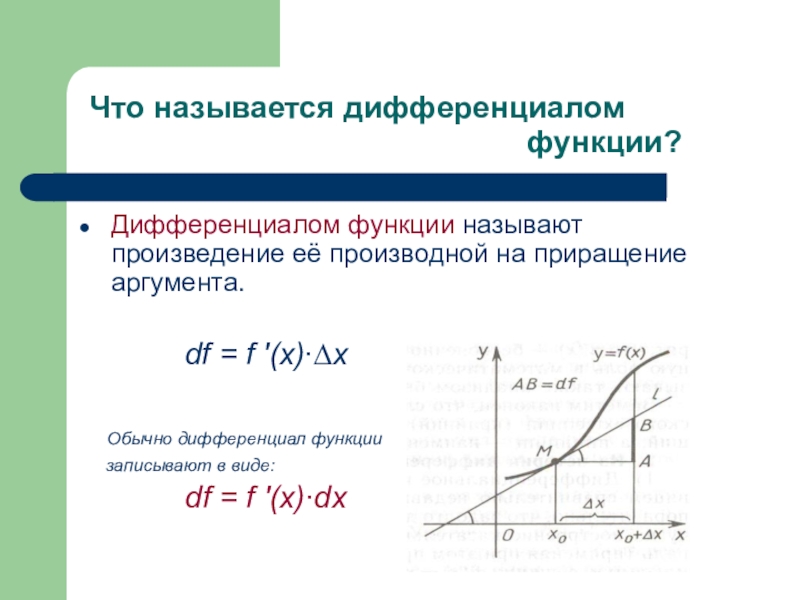
Дифференциалом функции называют произведение её производной на приращение аргумента.
df = f ′(x)∙∆x
Обычно дифференциал функции
записывают в виде:
df = f ′(x)∙dx
Слайд 7
Производная – одно из фундаментальных понятий математики. Оно возникло в XVII в. в связи с необходимостью решения ряда задач из физики, механики и математики, но в первую очередь для определения скорости прямолинейного движения и построения касательной к кривой.
Независимо друг от друга И.Ньютон и Г. Лейбниц разработали аппарат исчисления, которым мы пользуемся в настоящее время. Ньютон исходил в основном из задач механики (опирался на физическое представление о мгновенной скорости движения, считая его очевидным и, сводя к нему другие случаи производной), а Лейбниц по преимуществу исходил из геометрических задач (использовал понятие бесконечно малой).
Исчисление, созданное Ньютоном и Лейбницем, получило название дифференциального исчисления.
Слайд 8 Сведения из
Лозунгом многих математиков XVII в. был: «Двигайтесь вперёд, и вера в правильность результатов к вам придёт».
Термин «производная» - ( франц. deriveе - позади, за) ввёл в 1797 г. Ж . Лагранж. Он же ввёл современные обозначения y ' , f '
Обозначение lim –сокращение латинского слова limes (межа, граница). Термин «предел» ввёл И. Ньютон.
И. Ньютон называл производную флюксией, а саму
функцию - флюентой.
Г. Лейбниц говорил о дифференциальном
отношении и обозначал производную так:
Лагранж Жозеф Луи (1736-1813)
французский математик и механик
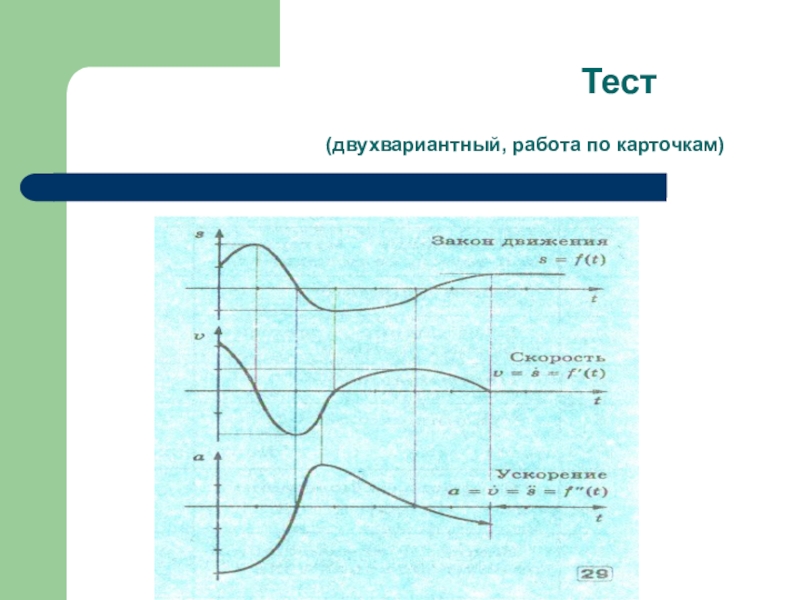
Слайд 9 Физический смысл производной.
Скорость есть производная от пути по
v(t) = x′(t)
Ускорение есть производная скорости по времени.
a(t) = v′(t) = x′′(t)
Слайд 10 Геометрический смысл
Угловой коэффициент касательной к графику функции равен производной этой функции, вычисленной в точке касания.
f′(x) = k = tga
Слайд 11 Дифференциал
Сила – производная работы по перемещению.
Сила тока – производная заряда по времени.
Линейная плотность – производная массы (тонкого стержня) по длине.
Теплоёмкость – производная теплоты по температуре.
Мощность – производная работы по времени.
Слайд 12 Кроссворд
По вертикали:
1.Создатель дифференциального исчисления, использовавший понятие бесконечно малой.
2. Коэффициент пропорциональности между
3. Создатель дифференциального исчисления, опирающийся на физическое представление о мгновенной скорости, считавший его очевидным и сводящий к нему другие случаи производной.
4. Производная от работы по времени.
5.Производная от количества электричества по времени - …?…. тока.
По горизонтали:
Производная от скорости по времени.
Производная от пути по времени.
Производная от массы неоднородного стержня по длине – линейная …….?……. .
Слайд 14Домашнее задание.
Стр.137 рис.100, пример 7, разобрать, записать вывод свойства параболы, имеющее
Стр. 138, № 269, 270, 271.
Слайд 15 Найти скорость и ускорение для точки, движущейся по закону в
Задача