Георгиевна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Несинусоидальные токи и напряжения
Содержание
- 1. Несинусоидальные токи и напряжения
- 2. Периодическими несинусоидальными токами и напряжениями называют токи и напряжения, изменяющиеся во времени по периодическому несинусоидальному закону.
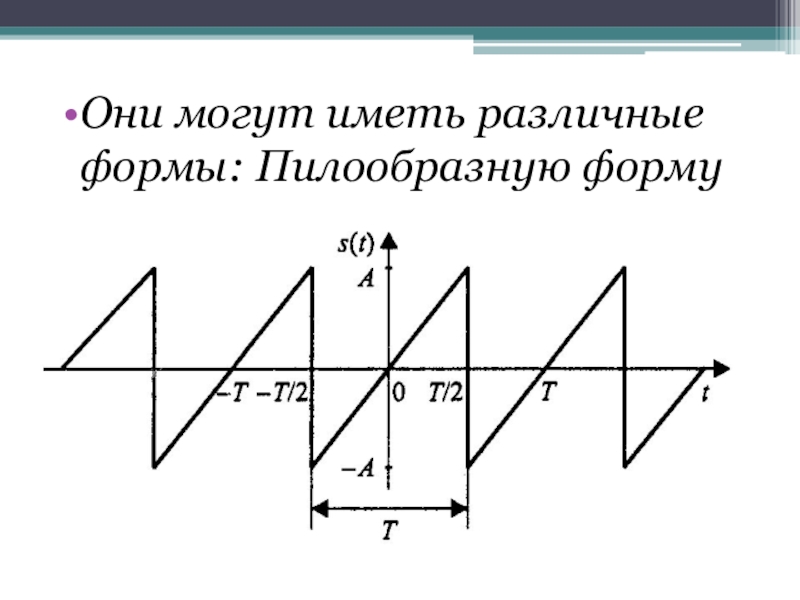
- 3. Они могут иметь различные формы: Пилообразную форму
- 4. Прямоугольная форма
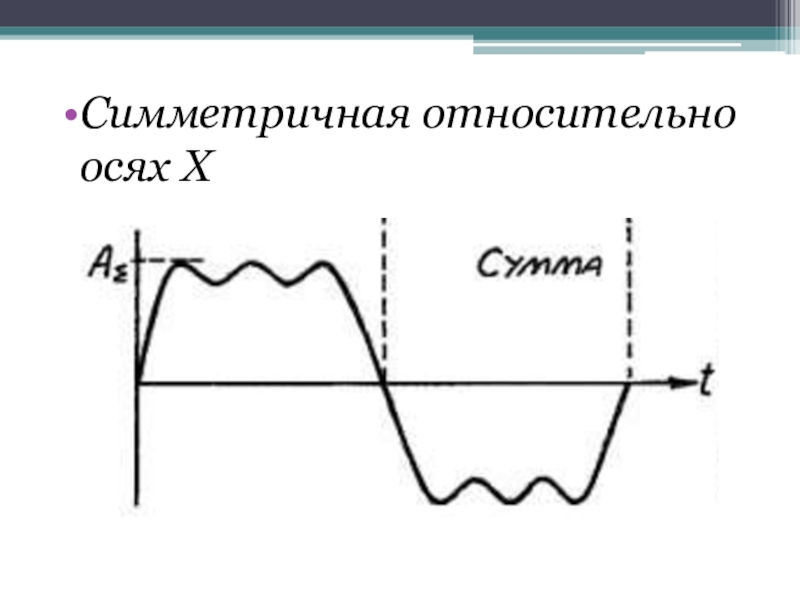
- 5. Симметричная относительно осях X
- 6. Трапециодальная форма
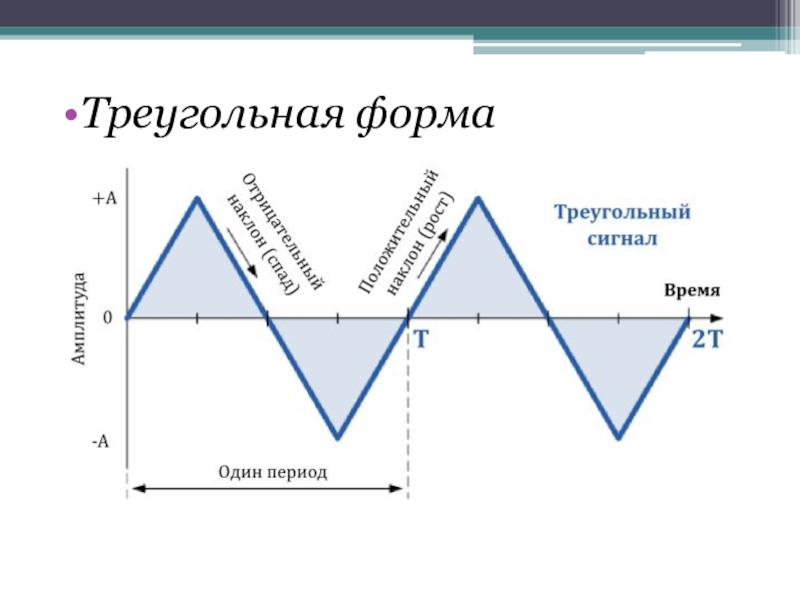
- 7. Треугольная форма
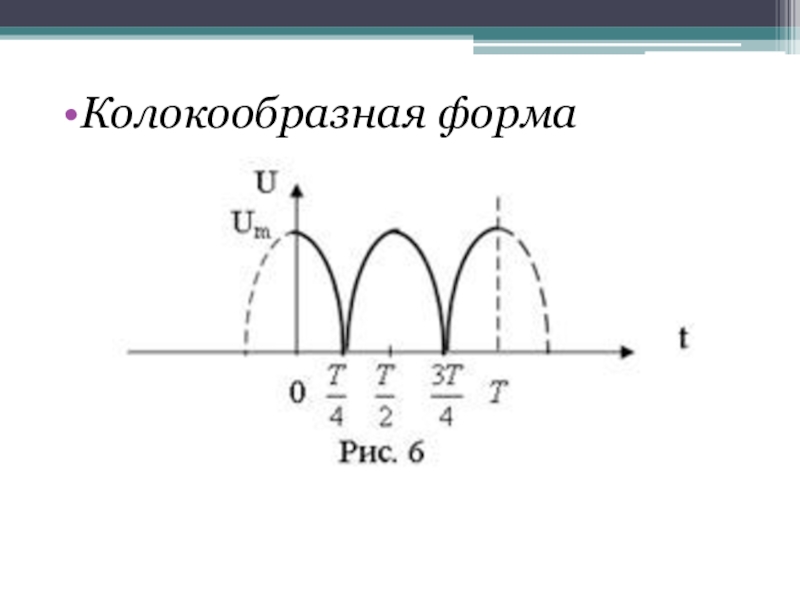
- 8. Колокообразная форма
- 9. Все электростанции вырабатывают синусоидальный ток , а эти несинусоидальные токи получаются из синусоидальных
- 10. Причины возникновения несинусоидальных токов и напряжений 1)
- 11. 3) Из-за подключения к сети генератора на
- 12. Аналитические выражения несинусоидальной периодической величиныНе синусоидальные периодические
- 13. ί= I0 + ί1 + ί2 +
- 14. Первая гармоническая составляющая имеет период ,равный периоду
- 15. Нельзя судить о номере гармоники только по
- 16. Действующие значения несинусоидального токаОпределяется по тому же
- 17. Действующее значения синусоидального переменного тока численно равно
- 18. Q= I2 * R * T –
- 19. Всё сложим:I2 * R * T =
- 20. Отсюда следует, что действительная величина несинусоидального тока
- 21. Пример Ток изменяется по закону:ί = 282
- 22. Левую и правую часть уравнения (1) сократим
- 23. Задача:Ток изменяется по следующему закону:ί = 242
- 24. I3 = Im3 / =
Периодическими несинусоидальными токами и напряжениями называют токи и напряжения, изменяющиеся во времени по периодическому несинусоидальному закону.
Слайд 1Электрические цепи с несинусоидальными токами и напряжениями
Материал подготовила преподаватель:
Махиня Альбина
Слайд 2Периодическими несинусоидальными токами и напряжениями называют токи и напряжения, изменяющиеся во
времени по периодическому несинусоидальному закону.
Слайд 9Все электростанции вырабатывают синусоидальный ток , а эти несинусоидальные токи получаются
из синусоидальных
Слайд 10Причины возникновения несинусоидальных токов и напряжений
1) При последовательном включении нескольких
генераторов синусоидальной ЭДС с кратными частотами( т.е. частоты отличаются в целое число раз)
2) Несовершенство источников питания (Зазоре между роторами и статором магнитная индуктивность распределается по синусоидальному закону )
2) Несовершенство источников питания (Зазоре между роторами и статором магнитная индуктивность распределается по синусоидальному закону )
Слайд 113) Из-за подключения к сети генератора на синусоидального напряжения специальной формы(
Блокинг генераторы, мультивибратор , триггер )
4) Из-за наличия в электрической цепи нелинейных элементов (полупроводниковые диоды, катушки индуктивности с ферритовыми сердечниками)
4) Из-за наличия в электрической цепи нелинейных элементов (полупроводниковые диоды, катушки индуктивности с ферритовыми сердечниками)
Слайд 12Аналитические выражения несинусоидальной периодической величины
Не синусоидальные периодические функции, так как и
синусоидальное наглядно изображается виде графиков. Для расчётов требуется аналитические выражения несинусоидальных функций, которые осуществляется с помощью теоремы Фурье, согласно которой любая периодическая функция y(ωt) может быть представлена в виде суммы ряда состовляющих, из которых одна состовлящяя постоянная, а другая является синусоидальными функциями с кратными частотами- гармоническими состовляющим просто гармониками.
Слайд 13ί= I0 + ί1 + ί2 + … + ίn =
I0 + Im1 sin(ωt+ψ1) + Im2 sin(2ωt+ψ2)+ … In sin(nωt+ψn)
Где I0 – постоянная состовляющая;
Im1 sin(ωt+ψ1) – основная гармоника она имеет наибольшую амплитуду (без учёта резонанса) и её период равен периоду изменения на sin20 тока.
ί1 , ί2 , ί3 и т.д. гармоники несинусоидального тока.
1ая , 2ая , 3ая и т.д. амплитуды гармонические составляющих.
С увеличением номера гармоники её амплитуда уменьшается (без учёта резонанса), а частота возрастает в целое число раз по сравнению с основной гармоникой (т.е. ω, 2ω, 3ω … nω)
ψ1 , ψ2 , ψ3 … ψn – начальные фазы гармоник.
Где I0 – постоянная состовляющая;
Im1 sin(ωt+ψ1) – основная гармоника она имеет наибольшую амплитуду (без учёта резонанса) и её период равен периоду изменения на sin20 тока.
ί1 , ί2 , ί3 и т.д. гармоники несинусоидального тока.
1ая , 2ая , 3ая и т.д. амплитуды гармонические составляющих.
С увеличением номера гармоники её амплитуда уменьшается (без учёта резонанса), а частота возрастает в целое число раз по сравнению с основной гармоникой (т.е. ω, 2ω, 3ω … nω)
ψ1 , ψ2 , ψ3 … ψn – начальные фазы гармоник.
Слайд 14Первая гармоническая составляющая имеет период ,равный периоду несинусоидальной кривой Im(ωt). Она
называется первой, или основной , гармоникой .
Все другие гармонические составляющие имеют частоты, в целое раз число больше частоты первой гармоники. Эти гармоники называются Высшими.
В этом законе содержатся все компоненты, т.е. все чётные и все нечётные гармоники, но бывают случай, когда присутствуют только чётные гармоники.
Все другие гармонические составляющие имеют частоты, в целое раз число больше частоты первой гармоники. Эти гармоники называются Высшими.
В этом законе содержатся все компоненты, т.е. все чётные и все нечётные гармоники, но бывают случай, когда присутствуют только чётные гармоники.
Слайд 15Нельзя судить о номере гармоники только по её месту в уравнении,
а надо проследить все последующие, т.е. она может быть 3ей , а может следующая 5ой , затем 7ой и т.д., т.е.нечётные или только чётные.
В электротехнике присутствует только 3 вида несинусоидальных кривых
- Симметричные относительно оси X
- Симметричные относительно оси Y
- Симметричные относительно начала координат.
В электротехнике присутствует только 3 вида несинусоидальных кривых
- Симметричные относительно оси X
- Симметричные относительно оси Y
- Симметричные относительно начала координат.
Слайд 16Действующие значения несинусоидального тока
Определяется по тому же принципу что и действующее
значение синусоидального тока.(Но не точно так же , а по тому же принципу)
Слайд 17Действующее значения синусоидального переменного тока численно равно такому постоянному току, при
котором выделяется столько же тепловой энергии, сколько при переменном токе в одном и том же резисторе за одинаковое время, равное одному периоду T. Из такого же условия определяют следующее значение переменного несинусоидального тока.
Слайд 18Q= I2 * R * T – Количество теплоты, которое выделяется
за один период T при несинусоидальном токе . ( где I2 – действующее значение sin-го тока)
Q0= I02 * R * T – Количество теплоты, которую выделяет постоянная составляющая за тоже время.
Qn= In2 * R * T - Количество теплоты, которую выделяет постоянная составляющая за время периода T при токе равном n-ной составляющей выделяется тепло (где Qn – количество теплоты n-ной гармоники. In2 – n-ная гармоника действующей величины тока.
Q0= I02 * R * T – Количество теплоты, которую выделяет постоянная составляющая за тоже время.
Qn= In2 * R * T - Количество теплоты, которую выделяет постоянная составляющая за время периода T при токе равном n-ной составляющей выделяется тепло (где Qn – количество теплоты n-ной гармоники. In2 – n-ная гармоника действующей величины тока.
Слайд 19Всё сложим:
I2 * R * T = I02 * R *
T + I12 * R * T + I22 * R * T + … + In2 * R * T (1)
I2 = I02 + I12 + I22 + … + In2
I2 = I02 + I12 + I22 + … + In2
Слайд 20Отсюда следует, что действительная величина несинусоидального тока явл. сл средней квадратичной
из постоянной составляющей и действующих величин синусоидальных составляющих этого тока:
Слайд 21Пример
Ток изменяется по закону:
ί = 282 sin ωt + 141
sin (3ωt – 560) + 70 sin (5ωt – 300) А
Определить действующее значение тока.
1) Найдём действующее значение 1ой гармоники
I1 = Im1 / = 282 / = 200 А
2) I3 = Im3 / = 1,41 /1,41 = 100 А
3) I5 = Im5 / = 70 /1,41 = 50 А
4 ) I = = = 205 А)
Определить действующее значение тока.
1) Найдём действующее значение 1ой гармоники
I1 = Im1 / = 282 / = 200 А
2) I3 = Im3 / = 1,41 /1,41 = 100 А
3) I5 = Im5 / = 70 /1,41 = 50 А
4 ) I = = = 205 А)
Слайд 22Левую и правую часть уравнения (1) сократим на T и получим
уравнения активных мощностей:
I2 * R = I02 * R + I12 * R + I22 * R + … + In2 * R
Или P = P0 + P1 + P2 + … + Pn – уравнение активных мощностей
Активная мощность в цепи не sin- ного тока равна сумме активных мощностей , соответветствующих постоянной величиной составляющей и отдельными гармоникам.
I2 * R = I02 * R + I12 * R + I22 * R + … + In2 * R
Или P = P0 + P1 + P2 + … + Pn – уравнение активных мощностей
Активная мощность в цепи не sin- ного тока равна сумме активных мощностей , соответветствующих постоянной величиной составляющей и отдельными гармоникам.
Слайд 23Задача:
Ток изменяется по следующему закону:
ί = 242 sin ωt + 141
sin 3ωt + 71 sin (ωt+300) А
Определить: Действующее значение тока.
В состав уравнения входит только нечётные гармоники: 1ая , 3ей , 5ая .
I =
Прежде всего определить действующие значения каждого тока.
I1 = Im1 / = 242 / = 172 А
Определить: Действующее значение тока.
В состав уравнения входит только нечётные гармоники: 1ая , 3ей , 5ая .
I =
Прежде всего определить действующие значения каждого тока.
I1 = Im1 / = 242 / = 172 А