- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Механические колебания и волны
Содержание
- 1. Механические колебания и волны
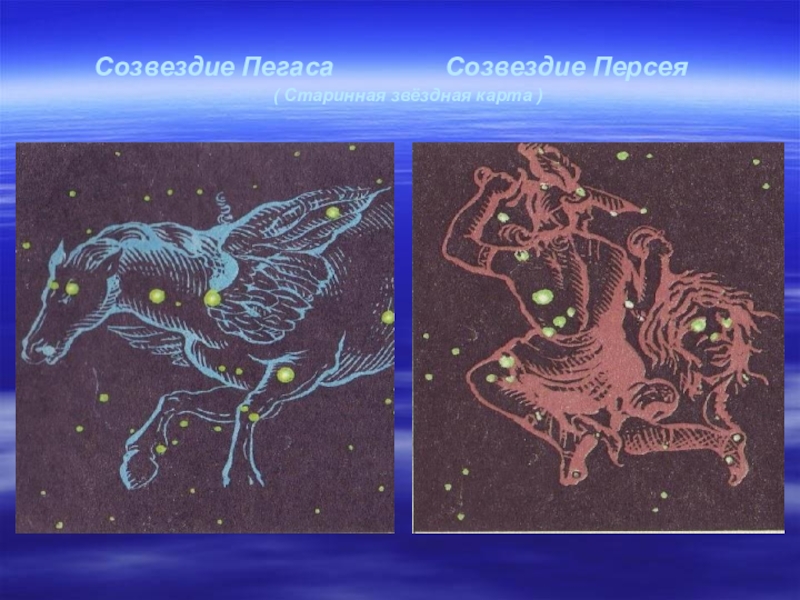
- 2. Созвездие
- 3. Урок 1.
- 4. Звёзды имеют разную яркость и цвет: белый,
- 5. 1 парсек = 3,26 светового года =
- 6. Слайд 6
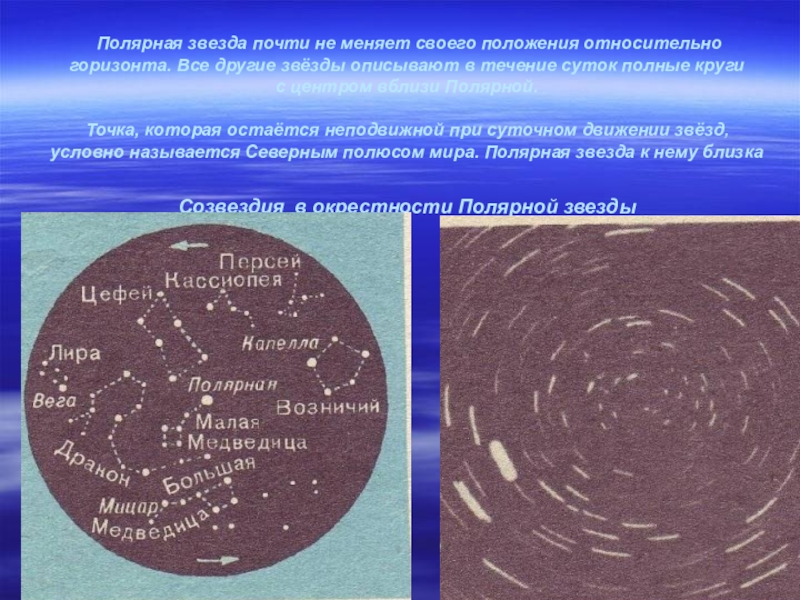
- 7. Полярная звезда почти не меняет своего
- 8. Вопросы для самоконтроля 1. Что называется
- 9. Тема: Небесные координаты. Эклиптика. Цель: Объяснить принцип
- 10. Небесная сфера – это воображаемая сфера произвольного
- 11. Экваториальные координаты. Небесные координаты определяют положение небесных
- 12. Прямое восхождение обозначается α. Его отсчитывают по
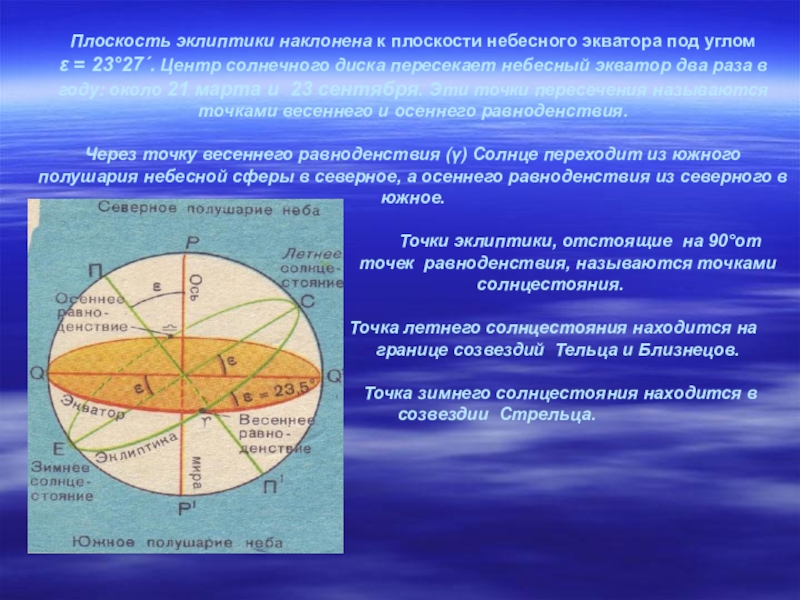
- 13. Плоскость эклиптики наклонена к плоскости небесного экватора
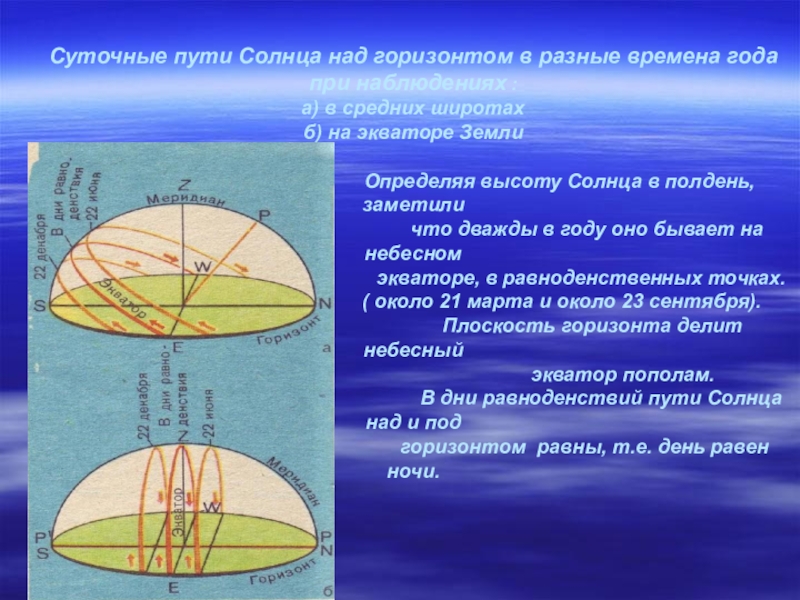
- 14. Суточные пути Солнца над горизонтом в разные
- 15. Кульминации светил – самое высокое и самое
- 16. Высота светила в верхней кульминации.
- 17. Вопросы для самоконтроля: 1. Можно
- 18. Тема: Календарь. Местное и поясное время. Цель:
- 19. Календарь – система отсчета длительных промежутков времени.
- 20. Некоторые задачи практической астрономии.
- 21. Слайд 21
- 22. Законы Кеплера.
- 23. Чтобы определить форму траектории и закономерности в
- 24. Эллипсом называется плоская замкнутая кривая, имеющая такое
- 25. Второй закон Кеплера. ( закон площадей )
- 26. Третий закон Кеплера. Квадраты звёздных периодов
- 27. Вопросы для самоконтроля. 1. Что утверждает
- 28. Тема: Методы определения расстояния в астрономии. Цель:
- 29. Горизонтальный параллакс. Угол,
- 30. Расстояние SС = D = R /
- 31. Годичный параллакс. Для определения расстояний до
- 32. Расстояние до звезды, годичный параллакс которой равен
- 33. Радиолокационный метод Этот метод
- 34. Определение размеров тел Солнечной системы. Углы,
- 35. Вопросы для самоконтроля: 1.
- 36. Литература: 1. Б.А. Воронцов – Вельяминов, М.М.Дагаев,
- 37. Данное пособие разработано для учащихся 9-х
Слайд 1Тема: Небесная сфера и небесные координаты.
Урок 1. Звездное небо.
Урок 2.
Урок 3. Календарь. Местное и поясное время.
Урок 4. Законы Кеплера.
Урок 5. Определение расстояний и размеров тел в солнечной системе.
Слайд 3Урок 1. Тема: Звездное небо. Цель: Познакомить учащихся с созвездиями и наиболее
Слайд 4Звёзды имеют разную яркость и цвет: белый, желтый, красноватый. Чем краснее
звезда, тем она холоднее. Наше Солнце относится к жёлтым звёздам.
В 1603 году Иоганн Байер начал обозначать яркие звезды каждого
созвездия буквами греческого алфавита в порядке убывания их
блеска. Эти обозначения используются и в наши дни.
Самые яркие звёзды ещё в древности назвали звёздами 1-й величины, а самые слабые
видимые на пределе зрения, - звёздами 6-й величины.
Звёздная величина ( обозначается m ) – характеризует световой поток, приходящий на Землю от звезды. Принято, что при разности в одну звёздную величину видимая яркость звёзд отличается примерно в 2,5 раза.
Звёзды 1-й величины в 100 раз ярче звёзд 6-й величины. Современные методы наблюдений дают возможность обнаружить звёзды до 25-й звёздной величины.
Точные измерения показывают, что звёзды имеют как дробные, так и отрицательные звездные величины.
Слайд 51 парсек = 3,26 светового года = 206265 а.е. = 3·10'³км.
которую имела бы звезда, находясь на стандартном расстоянии в 10 парсек.
Расстояние, которое свет проходит в течение года, называется
световым годом.
Связь абсолютной звёздной величины М и видимой звёздной величины т
с расстоянием до звезды R в парсеках выражается формулой
M = m + 5 – 5 Įg R
Слайд 6
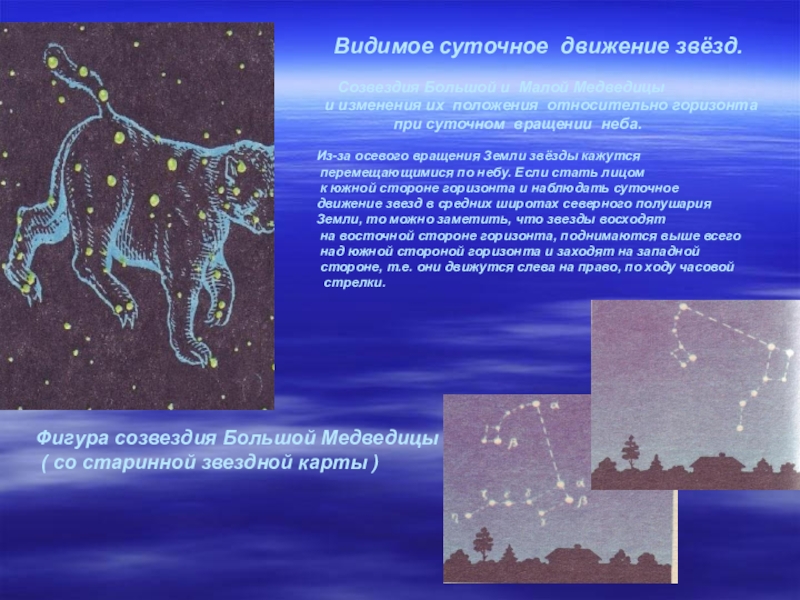
Слайд 7 Полярная звезда почти не меняет своего положения относительно горизонта. Все другие
Слайд 8Вопросы для самоконтроля
1. Что называется созвездием?
2. Сколько
3. Как обозначаются звёзды в созвездиях?
4. Что определяет звёздная величина?
Слайд 9Тема: Небесные координаты. Эклиптика. Цель: Объяснить принцип определения положения светил на небе
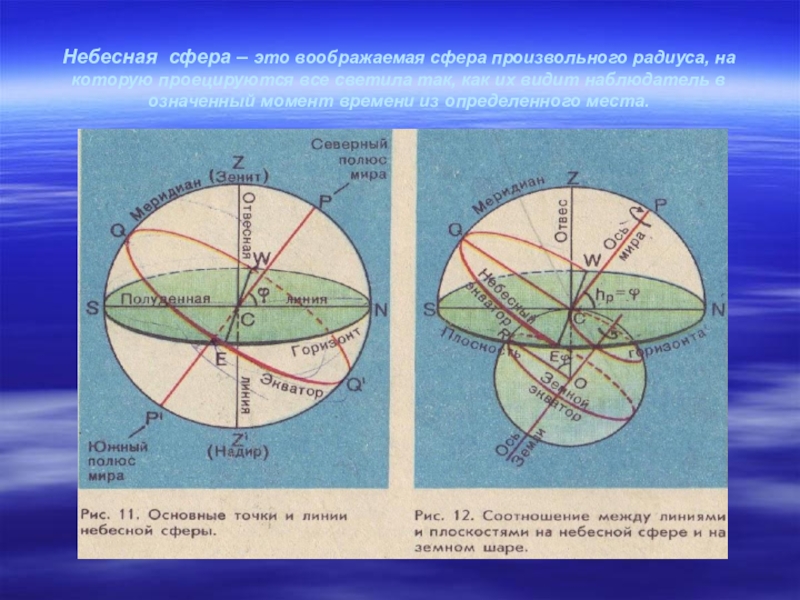
Для удобства измерений и решения практических задач по определению положения звёзд, движения планет и т.д. в астрономии используется понятие - небесная сфера.
На небесной сфере рассматривают лишь угловые расстояния.
Угловым расстоянием называется расстояние, измеряемое дугой или соответствующим ей центральным углом между двумя точками сферы.
Слайд 10Небесная сфера – это воображаемая сфера произвольного радиуса, на которую проецируются
Слайд 11Экваториальные координаты. Небесные координаты определяют положение небесных тел на небесной сфере. Они
Слайд 12Прямое восхождение обозначается α. Его отсчитывают по дуге небесного экватора от
Слайд 13Плоскость эклиптики наклонена к плоскости небесного экватора под углом ε =
Слайд 14Суточные пути Солнца над горизонтом в разные времена года при наблюдениях
Слайд 15Кульминации светил – самое высокое и самое низкое положение светила относительно
Слайд 16Высота светила в верхней кульминации.
Слайд 17Вопросы для самоконтроля: 1. Можно ли определить по картине вращения звездного
Слайд 18Тема: Календарь. Местное и поясное время. Цель: Дать понятие о методах счета
Солнечные сутки – это промежуток времени между двумя последовательными одноимёнными кульминациями Солнца.
Местное солнечное время – это время определяемое прохождением Солнца через местный меридиан, которое справедливо только для данной географической долготы.
Поверхность Земли условно разделена меридианами на 24 часовых пояса, каждый из которых простирается по долготе на 15°, или 1ч.
Начальный меридиан, от которого ведется счет долгот на Земле, проходит через Гринвич ( Великобритания). Он считается нулевым меридианом, а его временной пояс принят за нулевой часовой пояс.
Местное солнечное время Гринвичского меридиана принято в качестве всемирного времени.
Через территорию Казахстана проходят 4-й и 5-й часовые пояса.
Зная всемирное время (Т ) и порядковый номер пояса ( п ) можно найти поясное время любого места.
Астана и Алматы находятся в одном часовом поясе (5-м), который опережает всемирное время на 6 часов.
Местное солнечное время на географической долготе λ к востоку от Гринвича определяется добавлением ко всемирному времени значение долготы в часах.
Слайд 19Календарь – система отсчета длительных промежутков времени. Основой для ведения счета времени
Календари делятся на 3 типа: солнечные, лунные, лунно-солнечные.
Астрономический год приближенно равен 365 суткам 5 часам 48 минутам 46секундам.
В календаре введенном Юлием Цезарем в 46г.до н.э. продолжительность года принималась округлённо равной 365 суткам 6 часам. Каждые 4 года «довесок» в 6 часов накапливал одни сутки ( 24ч. ), которые прибавлялись к году. Так получался « високосный» год, содержащий в феврале 29 дней.
Разница между юлианским и астрономическим годом ( 11мин.14с) каждые 128 лет становилась равной одним суткам и к 16 веку стала весьма заметной. За 400 лет старый стиль отставал от действительного течения времени примерно на 3 суток.
В конце 16 века был введен новый календарь ( григорианский) в котором учитывалась ошибка прежнего, юлианского календаря.
В григорианском календаре (новом стиле), введенном в СССР в 1918 году годы оканчивающиеся на два нуля, за исключением 1600, 2000, 2400 и т.п. (т.е. тех, у которых число сотен делится на 4 без остатка ), не считаются високосными. Этим и исправляют ошибку в 3 суток, накапливающуюся за 400 лет.
К 20 веку разница между новым стилем и старым ( юлианским) достигла 13 суток. Разница в 13 суток сохранится и 21 веке, а в 22 веке возрастёт до 14 суток.
По новому стилю ошибка в 1 сутки накопится за 3300 лет.
Слайд 20Некоторые задачи практической астрономии.
Современное общество не
Строительство каналов, железных и шоссейных дорог начинается с астрономических наблюдений, позволяющих проложить на местности трассу, намеченную к строительству.
В последние годы прокладываются газо- и нефтепроводы протяженностью тысячи километров. В прокладке этих трасс участвуют астрономы – геодезисты, показывающие их направления.
Сейчас астрономическая ориентировка широко применяется в космонавтике. Для ориентировки автоматических космических аппаратов используются Солнце, Луна и яркие звезды ( Капелла, Вега, Канопус), координаты которых хорошо известны.
Переданная на Землю радиоинформация обрабатывается, и по этим результатам с Земли подаётся команда на корректирующие двигатели, ориентирующие корабль в нужном направлении. Те же светила используются космонавтами для определения координат пилотируемых кораблей.
Слайд 21
1. В чём разница между истинными и средними солнечными сутками?
2. Местному времени какого пункта на Земле соответствует всемир-
ное время?
3. Сколько часовых поясов и какие из них по номеру проходят через
территорию Республики Казахстан?
4. Одинаково ли местное время в двух столицах Казахстана? Что необ-
ходимо знать, чтобы рассчитать разницу местного времени между
этими городами?
5. Одинаково ли поясное время в Астане и Алматы?
Слайд 22Законы Кеплера.
Слайд 23Чтобы определить форму траектории и закономерности в движениях планет, он воспользовался
Результатом многолетнего труда И.Коперника стало открытие в 1609 – 1619 гг.трех законов планетных движений.
Первый закон Кеплера
( определяет форму орбиты планеты )
Каждая планета обращается по эллипсу
в одном из фокусов которого находится
Солнце.
Слайд 24Эллипсом называется плоская замкнутая кривая, имеющая такое свойство, что сумма расстояний
Точка О – центр эллипса, K и S – фокусы. Солнце находится в данном случае в фокусе S.
DO = ОА = а - большая полуось эллипса.
Большая полуось является средним расстоянием планеты от Солнца:
а = DS + SA / 2
Ближайшая к Солнцу точка орбиты А называется перигелием , а самая далекая от него точка D – афелием.
Степень вытянутости эллипса характеризуется его эксцентриситетом е.
Эксцентриситет равен отношению расстояния фокуса от центра
( ОК =О S ) к длине большой полуоси а , т.е. е = О S / ОА
При совпадении фокусов с центром ( е = 0 ) эллипс превращается в окружность.
Эксцентриситет орбиты Земли е = 0,017.
Слайд 25Второй закон Кеплера. ( закон площадей ) Радиус – вектор планеты за одинаковые
Слайд 26Третий закон Кеплера. Квадраты звёздных периодов обращения планет относятся как кубы больших полуосей
Большая полуось орбиты а¹, звёздный период обращения одной планеты
Т¹, а другой планеты - а² и т², формула третьего закона :
Т1² / Т2² = а1³ / а2³.
Этот закон Кеплера связывает средние расстояния планет от Солнца с их
звёздными периодами и позволяет установить относительные расстояния
планет от Солнца, т.е. позволяет выразить большие полуоси всех планет-
ных орбит в единицах большой полуоси земной орбиты.
Большая полуось земной орбиты принята за астрономическую единицу
расстояний ( а = 1а.е. = 149 600 000км )
Слайд 27Вопросы для самоконтроля.
1. Что утверждает первый закон Кеплера?
3. В каких точках скорость движения планеты по орбите максимальна и
минимальна?
4. Как изменяется значение скорости движения планеты при её перемеще-
нии от афелия к перигелию?
5. Большая полуось орбиты Юпитера 5 а.е. Чему равен период его
обращения вокруг Солнца?
Слайд 28Тема: Методы определения расстояния в астрономии. Цель: Познакомить учащихся с основными методами
Слайд 29Горизонтальный параллакс.
Угол, под которым со светила
лярный к лучу зрения, называется горизонтальным параллаксом.
Чем больше расстояние до светила, тем меньше угол p.
Этот угол равен параллактическому смещению светила для наблюдателей, находящихся в точках А и В.
Угол САВ равен углу DСА, как углы при параллельных прямых
( DС ║ АВ по построению).
Угол САВ = p ( параллакс )
Расстояние СВ - базис
Слайд 30Расстояние SС = D = R / sin p R = 6378км
Горизонтальный параллакс Луны составляет 57´.
Все планеты и Солнце гораздо дальше, и их параллаксы составляют секунды дуги.
Параллакс Солнца p = 8,8״.
При малых углах sin p ≈ p, если угол выражен в радианах.
Если р выражен в секундах дуги, вводится множитель
sin 1״ = 1 / 206265, где
206265 – число секунд в одном радиане.
Тогда sin p = p sin l״ = p / 206265״
Следовательно расстояние
по известному параллаксу
D = 206265" · R / р
Слайд 31Годичный параллакс.
Для определения расстояний до звёзд, расположенных не на
из двух противоположных точек орбиты Земли.
В этих целях в качестве базиса используют радиус орбиты Земли.
Годичный параллакс – это угол π, под которым радиус земной орбиты, перпендикулярный к лучу зрения, был бы виден со звезды.
R – расстояние до звезды.
R = a / sin π
Годичный параллакс всех звёзд
очень мал: он всегда меньше 1״.
Звезда с годичным параллаксом
1״ находится на расстоянии от Земли:
R = 1а.е./ sin 1״ = 206265а.е. = 3,086·10¹³км
Слайд 32Расстояние до звезды, годичный параллакс которой равен 1", называется парсеком (
Самая ближайшая к Земле звезда Проксима ( α – Центавра)
Её годичный параллакс равен 0,76".
Значит, расстояние до неё равно R = 1,3 пк
Слайд 33Радиолокационный метод
Этот метод основан на отправлении в
отраженного от него сигнала.
Скорость распространения радиоволны равна скорости света в вакууме и составляет с = 299792458 м/с.
Радиолокационные наблюдения Венеры позволили определить астрономическую единицу с большой точностью:
1а.е.= 149597868 ± 0,7км
Слайд 34Определение размеров тел Солнечной системы.
Углы, под которыми видны наблюдателю
системы определяются с помощью специальных методов.
Т –центр Земли, М – центр светила линейного радиуса r.
По определению горизонтального параллакса радиус Земли
R виден со светила под углом р. Радиус светила r виден с Земли под углом ρ.
R = D sinρ; расстояние до него D = Rз / sinp, где
Rз – радиус Земли. D = r / sinρ , то r = sinρ·Rз / sinp, если
углы ρ и р малой величины, то r = Rз ρ / р.
( этот способ определения размеров применим только тогда, когда виден диск светила ).
Линейный радиус светила вычисляется : r = D sinρ, или r = Dρ,
если угол выражен в радианах.
Слайд 35Вопросы для самоконтроля:
1. В чем состоит сущность
2. Как измерить расстояние до некоторой удаленной точки методом
параллакса?
3. Что такое горизонтальный параллакс светила?
4. Что такое годичный параллакс звезды?
5. Как определить расстояние до некоторой звезды, используя
годичный параллакс?
Слайд 36Литература:
1. Б.А. Воронцов – Вельяминов, М.М.Дагаев, Э.В. Кононович.
2. Ф.Ю. Зигель. Звёздная азбука.(пособие для учащихся).
Изд.М.«Просвещение», 1981г.
3. Ф.Ю. Зигель. Сокровища звёздного неба. Изд.М.«Наука», 1980г.
4. П.И. Бакулин, Э.В. Кононович, В.И. Мороз. Курс общей астрономии.
Изд.М. «Наука», 1977г.
5. Б.А. Воронцов- Вельяминов. Астрономия ( учебник для 10кл.)
Изд.М. « Просвещение», 1987г.
Слайд 37
Данное пособие разработано для учащихся 9-х классов по теме
Тема рассчитана на 5 часов.
Составитель: Аберле Людмила Петровна,
учитель физики высшей категории,
Ленинской средней школы,
Аккайынского района.