- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Работа к НПК начальных классов Системы счисления
Содержание
- 1. Работа к НПК начальных классов Системы счисления
- 2. ВведениеЦель: познакомиться с различными системами
- 3. История возникновения системы счисленияЧеловек пользовался окружавшими его
- 4. Системы счисления Люди не могли обозначать
- 5. Непозиционные системы счисленияДревнеегипетская система счисления- 1205
- 6. Непозиционные системы счисленияРимская система счисленияПредполагаемое происхождение
- 7. Непозиционные системы счисленияНедостатки непозиционной системы счисленияПостоянная
- 8. Двадцатеричная система Древних майя
- 9. Вавилонская система счисленияЧисла в этой системе счисления
- 10. Двенадцатеричная система счисленияВозникла в древнем ШумереГипотезы возникновения:•
- 11. Позиционные системы счисленияДесятичная система счисления«Изобретена» индусами;
- 12. Позиционные системы счисленияДвоичная система счисления В
- 13. Правила перехода из одной системы счисления в
- 14. Правила перехода из двоичной системы счисления в
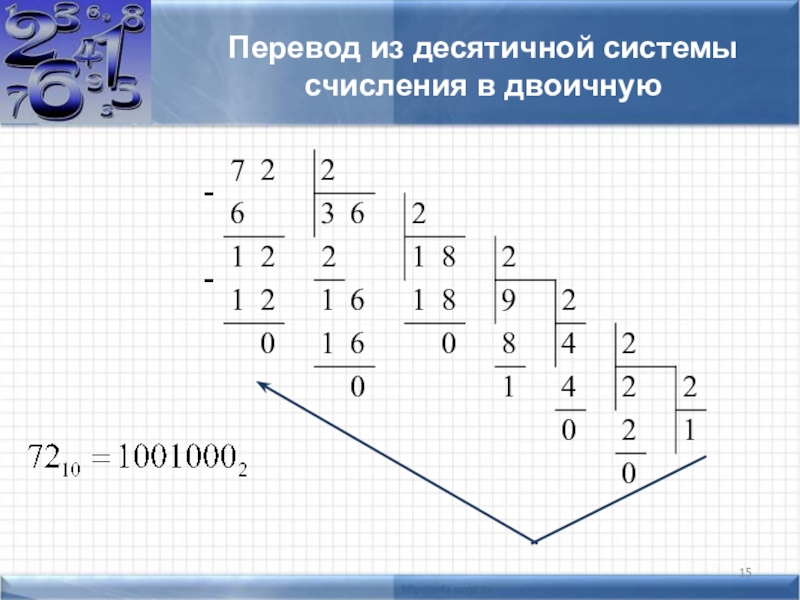
- 15. Перевод из десятичной системы счисления в двоичную
- 16. Перевод из двоичной системы счисления в десятичную
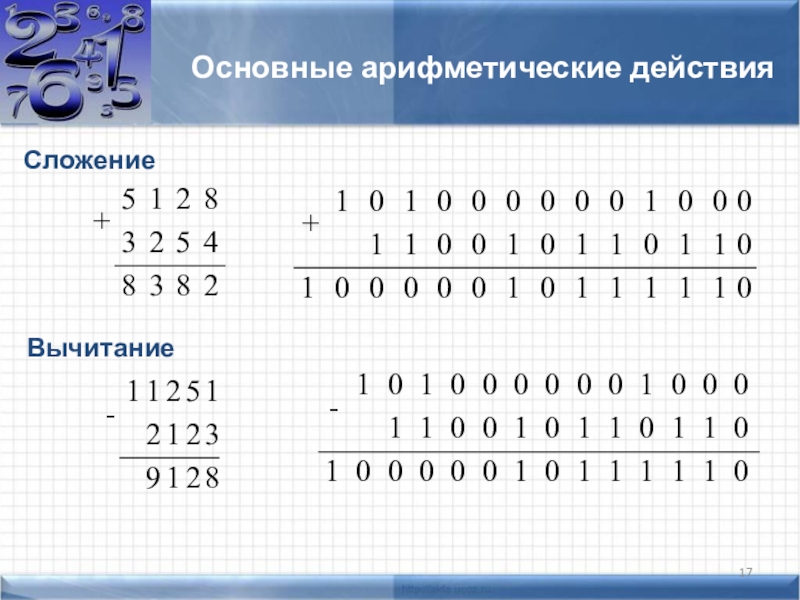
- 17. Основные арифметические действияСложениеВычитание
- 18. Основные арифметические действияУмножение
- 19. Основные арифметические действияДеление
- 20. Заключение Главное достоинство двоичной системы
- 21. Двоичная система имеет и
- 22. Спасибо за внимание!
Слайд 1Системы счисления.
Двоичная система счисления и основные арифметические действия в ней.
4 А класс
Слайд 2Введение
Цель:
познакомиться с различными системами счисления, узнать, для чего
Задачи:
изучить литературу о различных системах счисления,
выяснить почему в компьютерах информация представляется в двоичной системе счисления и чем она удобна,
где еще используется двоичная система счисления.
Слайд 3История возникновения системы счисления
Человек пользовался окружавшими его предметами как инструментами счета
Появление
Слайд 4Системы счисления
Люди не могли обозначать числа так, как им
СИСТЕМЫ СЧИСЛЕНИЯ
Непозиционные
Позиционные
Древнеегипетская
Римская
Древних майя
Вавилонская
Двенадцатеричная
Двоичная
Десятичная
Слайд 6Непозиционные
системы счисления
Римская система счисления
Предполагаемое происхождение цифр
Использование букв латинского алфавита
I
C – 100, D – 500, M – 1000.
264 – CCLXIV
Римская система счисления в наше время
номера глав в книгах, указание века,
числа на циферблате часов
Слайд 7Непозиционные
системы счисления
Недостатки непозиционной системы счисления
Постоянная потребность введения
новых знаков
чисел.
Сложность в выполнении
арифметических операций,
так как нет алгоритмов их
выполнения.
Слайд 8Двадцатеричная система Древних майя
1 2
Сначала использовали иероглифические символы.
Затем они стали записывать в виде точек и тире.
Точка означала единицы данного порядка, тире – пятерки.
Позиционные
системы счисления
Слайд 9Вавилонская система счисления
Числа в этой системе счисления составлялись из знаков двух
- обозначение единиц, - обозначение десятков.
- 3
- 20
- 52
Вавилонская система счисления в наше время
одна минута = 60 секунд, один час = 60 минут
Числа больше 60 записывались по разрядам, с пробелами
- 302
Позиционные
системы счисления
Слайд 10Двенадцатеричная система счисления
Возникла в древнем Шумере
Гипотезы возникновения:
• для счета использовались Фаланги
до 12 считали сидя, загибая 10 пальцев руки и 2 ноги.
Позиционные
системы счисления
Двенадцатеричная система счисления в наше время
1 год – 12 месяцев, чайные и столовые сервизы на 12 персон, в Англии в системе мер (1 фут = 12 дюймам).
Слайд 11Позиционные
системы счисления
Десятичная система счисления
«Изобретена» индусами;
в Европу ее занесли арабы
Ненаучная гипотеза происхождения
Количество углов соответствует числовому значению цифры: 0 – углов нет, 1 – один угол, 2 – два угла и т.д.
«Вес» цифры определяется ее позицией.
Слайд 12Позиционные
системы счисления
Двоичная система счисления
В записи числа участвуют только две
а число 2 представляет собой уже единицу следующего разряда.
100010 – 11111010002
Используется в различных областях техники
1 – включено, 0 – выключено
Недостаток
Быстрый рост числа разрядов, необходимых для записи чисел
Слайд 13Правила перехода из одной системы счисления в другую
Разделить десятичное число
Получится частное и остаток.
Частное опять разделить на 2.
Получится частное и остаток.
Выполнять деление до тех пор,
пока последнее частное
не станет меньшим 2.
Записать последнее частное
и все остатки в обратном порядке.
Полученное число и будет двоичной записью
исходного десятичного числа.
2310 = 101112
Правило перехода из десятичной с.с. в двоичную
Слайд 14Правила перехода из двоичной системы счисления в десятичную
Правило перехода из двоичной
Вклад единицы на первом месте справа есть число 1,
на втором – 2, на третьем – 4, на четвертом – 8 и т.д. Вклады нулей равны нулю.
1 0 1 1 12 = 16 + 4 + 2 + 1 = 2310
16 8 4 2 1
Слайд 20Заключение
Главное достоинство двоичной системы –
простота
Двоичная система счисления наиболее проста и удобна для автоматизации.
Из любой системы счисления можно перейти к двоичному коду.
Почти во всех компьютерах используют либо непосредственно двоичную систему счисления, либо двоичное кодирование какой-либо другой системы счисления.
Слайд 21 Двоичная система имеет и недостатки
ею пользуются только в
быстрый рост числа разрядов, необходимых для записи чисел.
Заключение