- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: Система работы над текстовой арифметической задачи в начальной школе
Содержание
- 1. Презентация по математике на тему: Система работы над текстовой арифметической задачи в начальной школе
- 2. Согласно стандартам нового поколения, выпускник начальной школы
- 3. Глобальной проблемой до сих пор является неумение
- 4. Учебники по математике тоже содержат большое количество
- 5. Но, к сожалению, учителя начальной школы часто
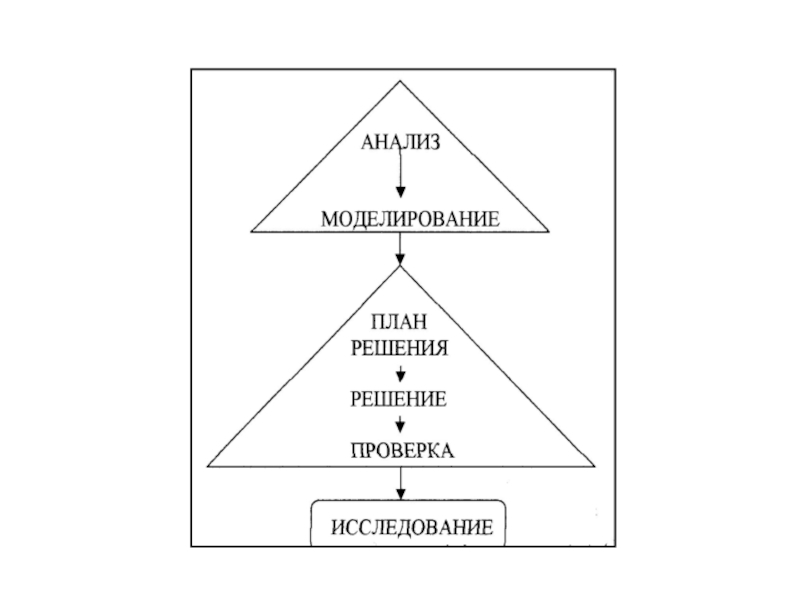
- 6. Схематично план решения арифметической задачи можно представить следующим образом:
- 7. Слайд 7
- 8. I ЭТАП ВОСПРИЯТИЕ И АНАЛИЗ ЗАДАЧИ Цель
- 9. Первый подэтап: 1) Чтение текста задачи: сначала
- 10. Второй подэтап (графическая работа с цветом): 4)
- 11. Вот как должен выглядеть текст задачи после
- 12. Третий подэтап: 6) Переформулировка текста задачи (отбрасывание
- 13. 7) Переконструирование текста задачи (У –В –
- 14. «Около школы росло 20 тополей. Сколько тополей
- 15. Дополнительно для обучения учащихся анализировать текст задачи можно использовать следующие упражнения:
- 16. 1) Анализ текстов задач с лишними и
- 17. 2) Анализ текстов задач с противоречивым условием.
- 18. 3) Анализ текстов задач с вопросом, в
- 19. 4) Анализ текстов задач с неопределённым условием.
- 20. 5) Сравнение текстов задач (сравниваются задачи, сходные
- 21. 6) Составление условия к данному вопросу. Составь
- 22. 7) Постановка вопроса к данному условию. Поставь
- 23. 8) Подбор условия к данному
- 24. Подбери вопрос к данному условию. «Дикие
- 25. I I этап - МОДЕЛИРОВАНИЕ
- 26. Моделирование - это замена действий
- 27. Для того, чтобы самостоятельно решать задачи,
- 28. Для формирования умения моделировать задачу, предлагаются следующие приёмы:
- 29. 1) Составление краткой записи задачи при помощи
- 30. 2) Выбор рисунка, схемы и т. д.
- 31. «В течение жизни человек спит 25 лет.
- 32. 3) Исправление ошибок в краткой записи задачи.
- 33. « В сосновом бору поселились 5
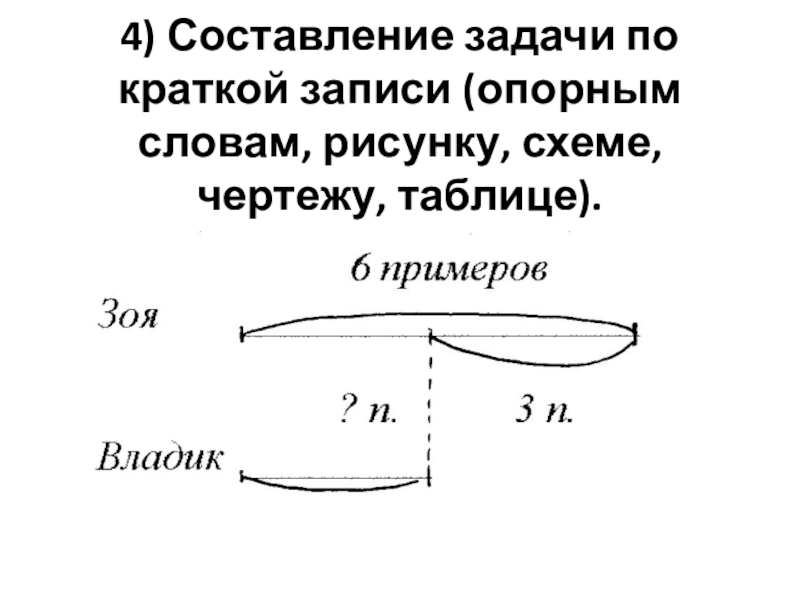
- 34. 4) Составление задачи по краткой записи (опорным словам, рисунку, схеме, чертежу, таблице).
- 35. 5) Подбор к схеме подходящего текста из предложенных. Подбери к схеме соответствующий текст задачи.
- 36. а) В конкурсе красоты приняли участие 5
- 37. 6) Установление взаимноодназначного соответствия – проведение «дорожек» от слова к его изображению на схеме.
- 38. Объясни данную схематическую модель в соответствии с
- 39. III ЭТАП ПОИСК И СОСТАВЛЕНИЕ ПЛАНА РЕШЕНИЯ ЗАДАЧИ
- 40. Самым важным на этом этапе является формирование
- 41. Чаще всего применяется аналитический способ рассуждения, но
- 42. 1) Разбор от вопроса к данным (
- 43. Чтобы помочь учащимся вести рассуждения аналитическим способом,
- 44. Можно оформить рассуждения в таблице. Учитель выдаёт
- 45. 2. Разбор от данных к вопросу
- 46. Для формирования умения выделять простые задачи
- 47. 1) Составь и реши простые задачи, используя
- 48. 2) Поставь вопрос к данному условию.
- 49. 3) Использование аналогии при поиске плана решения
- 50. 4) Поиск плана решения по модели
- 51. « С одного поля собрали 370
- 52. 5) Поиск плана решения путём составления уравнения
- 53. Схема уравнения: I
- 54. IV ЭТАП ЗАПИСЬ РЕШЕНИЯ И ОТВЕТА
- 55. Запись решения и ответа может производиться различными
- 56. Начиная с 3-го класса, решают каждую задачу
- 57. V ЭТАП ПРОВЕРКА РЕШЕНИЯ
- 58. Этот этап играет большую роль в развитии
- 59. Для проверки решения задач используются следующие приёмы:
- 60. Прикидка ответа или установление границ значений искомого
- 61. Установление соответствия между числами, полученными в результате
- 62. Составление и решение обратных задач. Этот способ
- 63. Решение задачи другим способом (если это возможно
- 64. VI ЭТАП ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА НАД ЗАДАЧЕЙ
- 65. Этот этап является очень важным и интересным,
- 66. Приёмы работы над задачей на данном этапе:
- 67. 1) Решение задачи другим способом (если это
- 68. 2) Составление аналогичной задачи с новыми данными.
- 69. 3) Постановка дополнительных вопросов к решённой задаче.
- 70. 4) Изменение вопроса задачи. - Измени вопрос
- 71. 5) Изменение условия задачи так, чтобы задача решалась другим действием.
- 72. 6) Изменение числовых данных задачи так, чтобы появился новый способ решения.
- 73. 7) Исследование решения. Сколько способов решения имеет
- 74. 8) Сравнение задач и их решения.
- 75. Кроме основного вида работы над задачей –
- 76. 1) Блиц-турниры Блиц-турнир предполагает устное решение
- 77. 2) Составление выражений, необходимых для решения задач с неопределёнными данными.
- 78. 3) Составление устного плана решения ( «Дерево
- 79. 5) Пояснение готовых способов решения задачи.
- 80. 6) Составление решения задачи разными способами в соответствии с данными пояснениями.
- 81. «От двух пристаней, находящихся на расстоянии
- 82. 7) Соотнесение пояснения с решением.
- 83. «Длина пришкольного участка прямоугольной формы 120 м
- 84. 8) Установление соответствия между содержанием задачи и
- 85. 9) Выбор среди нескольких схематических моделей
- 86. 11) Изменение текста задачи в соответствии с данным решением. 12) Нахождение ложного способа решения.
- 87. 13) Продолжение решения задачи.
- 88. 14) Объяснение выражений, составленных по данному условию.
- 89. 15) Составление выражений по вопросам к данному условию.
- 90. «На турбазе 8 маленьких палаток и 5
- 91. 16) Составление и определение смысла всевозможных выражений
- 92. Этот приём трудоёмкий, но очень полезный. При
- 93. 17) Составление задач: - по иллюстрации;
- 94. Слайд 94
- 95. Слайд 95
- 96. Слайд 96
- 97. Слайд 97
Согласно стандартам нового поколения, выпускник начальной школы должен владеть обобщёнными способами решения учебных задач, его необходимо научить осмысленно обрабатывать информацию, анализировать её, выявлять главное, «ядро» информации, устанавливать взаимосвязи между понятиями, проводить классификацию, сравнивать, делать обобщения. Это
Слайд 2Согласно стандартам нового поколения, выпускник начальной школы должен владеть обобщёнными способами
решения учебных задач, его необходимо научить осмысленно обрабатывать информацию, анализировать её, выявлять главное, «ядро» информации, устанавливать взаимосвязи между понятиями, проводить классификацию, сравнивать, делать обобщения. Это мыслительные операции, которые включает в себя словесно – логическое мышление. Этот тип мышления должен стать доминирующим к концу начальной школы.
Слайд 3Глобальной проблемой до сих пор является неумение учащихся решать задачи, находить
разные способы решения, действовать в нестандартных ситуациях, например, при выполнении тестовых работ, приобретающих с каждым годом всё большую популярность.
Слайд 4Учебники по математике тоже содержат большое количество упражнений, направленных на формирование
общеучебных умений, а именно:
1) выполнять семантический и математический анализ текстовых задач
(представлять ситуацию, описанную в тексте задачи, выделять данные и искомые величины, устанавливать взаимосвязи между ними);
2) представлять выявленные взаимосвязи в виде схематических и символических моделей (переводить словесную модель в символическую);
3) составлять план решения задачи посредством рассуждений;
4) проверять решение задачи;
5) проводить исследовательскую работу над задачей.
Слайд 5Но, к сожалению, учителя начальной школы часто отказываются от нетрадиционных методов
работы над задачей в силу трудоёмкости и ограниченности во времени в рамках 40-минутного урока. Во главу угла ставится количество решённых задач, а не качество работы, что влечёт за собой поверхностное отношение к текстам задач, действия по образцу, неумение выполнять задания с нестандартными формулировками.
Слайд 8I ЭТАП ВОСПРИЯТИЕ И АНАЛИЗ ЗАДАЧИ Цель этапа: понять задачу, представить, о чём
эта задача; установить, что
известно, что нужно найти, как связаны между собой данные и искомое.
Слайд 9Первый подэтап: 1) Чтение текста задачи: сначала про себя, затем вслух одним
из учеников.
2) Пересказ задачи своими словами (этот приём способствует более глубокому осмыслению прочитанного).
3) Представление жизненной ситуации, описанной в задаче, инсценировка этой ситуации.
Слайд 10Второй подэтап (графическая работа с цветом): 4) Разбиение текста задачи на смысловые
части, подчёркивание условия и вопроса синим и красным цветом, выделение числовых данных.
5) Выделение наиболее важных слов в каждой смысловой части и в вопросе задачи.
Слайд 11Вот как должен выглядеть текст задачи после этого подэтапа: «Лена нарисовала 10
шариков. 3 шарика она раскрасила красным цветом , синим – на 2 шарика больше , остальные шарики – зелёным цветом. / Сколько зелёных шариков на рисунке у Лены? (Синим цветом выделяем условие, красным – вопрос).
Слайд 12Третий подэтап: 6) Переформулировка текста задачи (отбрасывание несущественных деталей, зачёркивание). Этот приём
целесообразно использовать, если текст задачи объёмный и
содержит много несущественных деталей.
«В саду было 5 кустов облепихи. Когда посадили ещё несколько, то в саду стало 9 кустов облепихи. Сколько кустов посадили?»
«Было 5 кустов облепихи. Стало 9 кустов. Сколько кустов посадили?»
Слайд 137) Переконструирование текста задачи (У –В – У, В – У
– У У – В )
Важно как можно чаще использовать тексты нетипичных конструкций: текст задачи состоит из одного сложного вопросительного или повествовательного предложения, в котором стоит сначала вопрос, потом условие; часть условия представлена в начале текста, потом следует вопрос и другая часть условия; вместо слова «сколько» в вопросе используются слова «найди», «узнай» и т. д.).
Слайд 14«Около школы росло 20 тополей. Сколько тополей посадили осенью, если стало
43 тополя?» (У – В – У)
«Сколько кроликов было в клетке, если после того, как отсадили 7 cерых кроликов, осталось 5 белых кроликов?» (В – У – У)
«Узнай массу яйца кукушки, если оно на 1 грамм меньше яйца стрижа, которое весит 4 грамма»
Слайд 15Дополнительно для обучения учащихся анализировать текст задачи можно использовать следующие упражнения:
Слайд 161) Анализ текстов задач с лишними и недостающими данными. «На дереве
сидело 8 птичек. Сначала улетели 3 птички, потом ещё 2. Сколько птичек улетело?»
«На одном проводе сидели ласточки, а на другом – 7 воробьёв. Сколько всего сидело птиц на проводах?»
Слайд 172) Анализ текстов задач с противоречивым условием. «На одной клумбе растёт 10
хризантем, а на другой – 15. Сколько тюльпанов на двух клумбах?»
Слайд 183) Анализ текстов задач с вопросом, в котором спрашивается о том,
что уже известно.
«На клумбе росло 5 тюльпанов и 3 розы. Сколько тюльпанов росло на клумбе?»
Слайд 194) Анализ текстов задач с неопределённым условием. « В вазе лежало 3
яблока, 5 апельсинов, а груш на 2 меньше. Сколько всего фруктов в вазе?» (не указано, с чем сравнивается количество груш).
Слайд 205) Сравнение текстов задач (сравниваются задачи, сходные по сюжету, но разные
по математическому содержанию, либо с одинаковым математическим содержанием, но совершенно разных по сюжету).
«В вазе лежало 3 яблока, а апельсинов на 2 больше. Сколько апельсинов лежало в вазе?»
«В вазе лежало 3 яблока, их на 2 больше, чем апельсинов. Сколько апельсинов лежало в вазе?»
Слайд 216) Составление условия к данному вопросу. Составь условие к данному вопросу. «Сколько
марок в двух конвертах?»
«Сколько зебр привезли в зоопарк?»
Слайд 227) Постановка вопроса к данному условию. Поставь вопрос к данному условию. «В Тихом
океане 9 морей, а в Атлантическом на 3 моря меньше».
«В Тихом океане 9 морей, а в Индийском океане 5 морей».
Слайд 23 8) Подбор условия к данному вопросу или вопроса к данному условию.
Подбери условие к данному вопросу.
«Сколько кленовых листьев засушила Таня?»
а) Осенью Таня засушила 4 кленовых и 5 дубовых листьев.
б) Осенью Таня засушила 9 листьев. Из них 4 дубовых.
в ) Осенью Таня засушила 5 кленовых листьев, а дубовых на 4 больше.
г) Осенью Таня засушила 9 дубовых листьев, а кленовых на 4 меньше.
Слайд 24 Подбери вопрос к данному условию. «Дикие гуси живут 80 лет, а собаки
20 лет».
а) Сколько всего лет живут гуси и собаки?
б) На сколько лет гуси живут больше, чем собаки?
в) На сколько лет гуси живут меньше, чем собаки?
г) Сколько лет живут гуси?
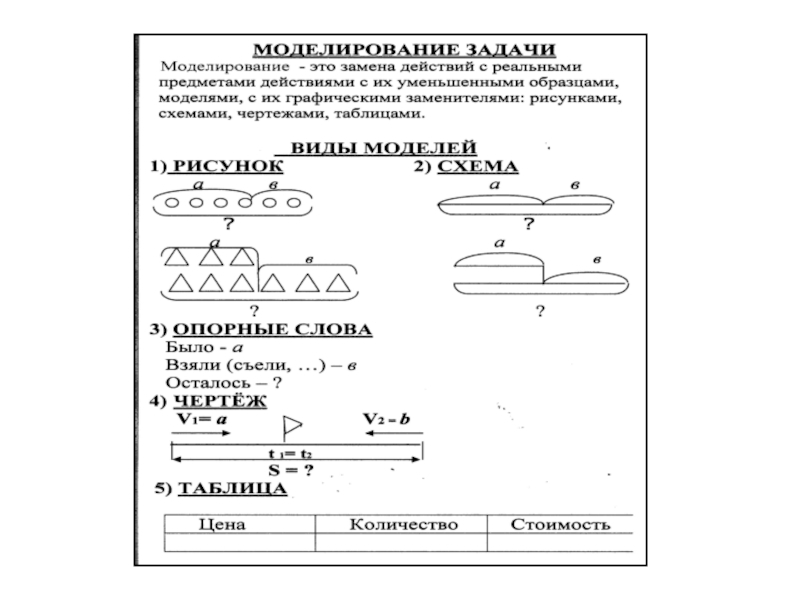
Слайд 26 Моделирование - это замена действий с реальными предметами действиями с уменьшенными
образцами, моделями, с их графическими заменителями: рисунками, схемами, чертежами, таблицами. Модель должна помочь ученику понять содержание задачи, выявить отношения между данными и искомым, найти разные способы решения задачи, увидеть новые,
не отражённые в задаче отношения.
Слайд 27 Для того, чтобы самостоятельно решать задачи, школьнику нужно освоить различные виды
моделей, научиться выбирать модель, соответствующую предложенной задаче и переходить от одной модели к другой. Наша задача – научить школьников применять тот способ моделирования, который наиболее подходит к той или иной задаче, помогает увидеть отношения между данными и искомым, найти разные способы решения задачи (если это возможно), увидеть скрытые взаимосвязи, не отражённые явно в тексте задачи.
Слайд 291) Составление краткой записи задачи при помощи опорных слов (рисунка, схемы,
таблицы и т. д.). Этот приём чаще всего используется на уроках в начальной школе.
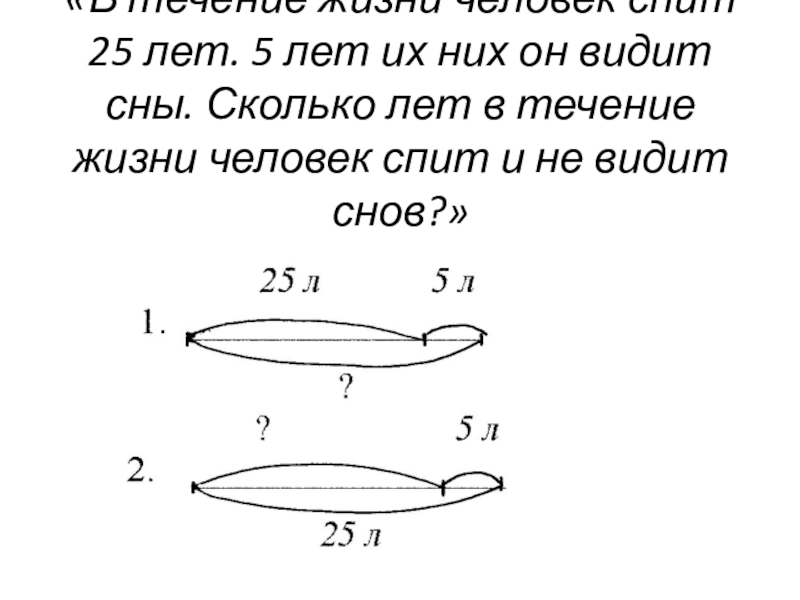
Слайд 31«В течение жизни человек спит 25 лет. 5 лет их них
он видит сны. Сколько лет в течение жизни человек спит и не видит снов?»
Слайд 323) Исправление ошибок в краткой записи задачи. Соответствует ли данная схема задаче?
Исправь ошибки в схеме, если они есть.
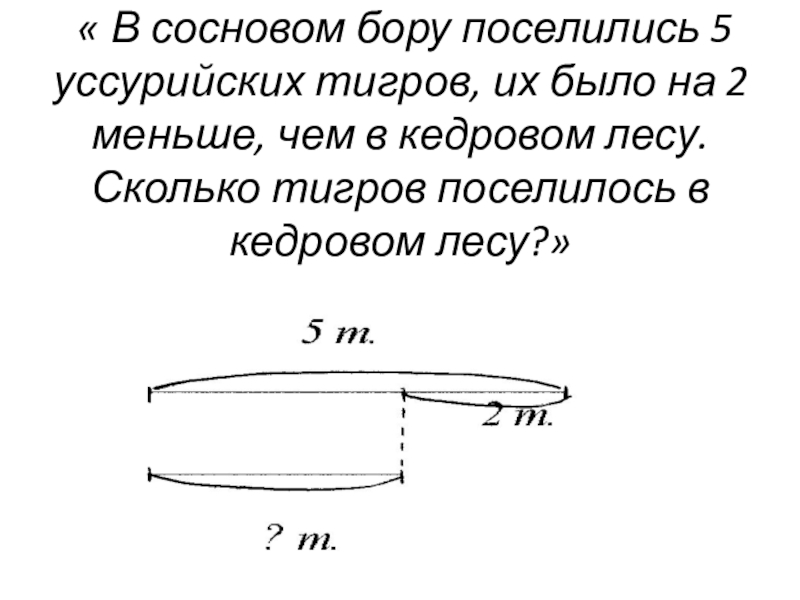
Слайд 33 « В сосновом бору поселились 5 уссурийских тигров, их было
на 2 меньше, чем в кедровом лесу. Сколько тигров поселилось в кедровом лесу?»
Слайд 355) Подбор к схеме подходящего текста из предложенных. Подбери к схеме соответствующий
текст задачи.
Слайд 36а) В конкурсе красоты приняли участие 5 бабочек махаонов, а бабочек
адмиралов – на 4 больше. Сколько адмиралов участвовало в конкурсе?
б) В конкурсе красоты приняли участие 9 бабочек адмиралов, а махаонов на 4 меньше. Сколько махаонов участвовало в конкурсе?
в) В конкурсе красоты приняли участие 5 бабочек махаонов, а бабочек адмиралов на 4 больше. Сколько всего бабочек приняли участие в конкурсе?
г) В конкурсе красоты приняли участие 5 бабочек махаонов, это на 4 меньше, чем бабочек адмиралов. Сколько адмиралов приняло участие в конкурсе?
д) В конкурсе красоты приняли участие 5 бабочек махаонов и 9 бабочек адмиралов. На сколько больше адмиралов приняли участие в конкурсе?
б) В конкурсе красоты приняли участие 9 бабочек адмиралов, а махаонов на 4 меньше. Сколько махаонов участвовало в конкурсе?
в) В конкурсе красоты приняли участие 5 бабочек махаонов, а бабочек адмиралов на 4 больше. Сколько всего бабочек приняли участие в конкурсе?
г) В конкурсе красоты приняли участие 5 бабочек махаонов, это на 4 меньше, чем бабочек адмиралов. Сколько адмиралов приняло участие в конкурсе?
д) В конкурсе красоты приняли участие 5 бабочек махаонов и 9 бабочек адмиралов. На сколько больше адмиралов приняли участие в конкурсе?
Слайд 376) Установление взаимноодназначного соответствия – проведение «дорожек» от слова к его
изображению на схеме.
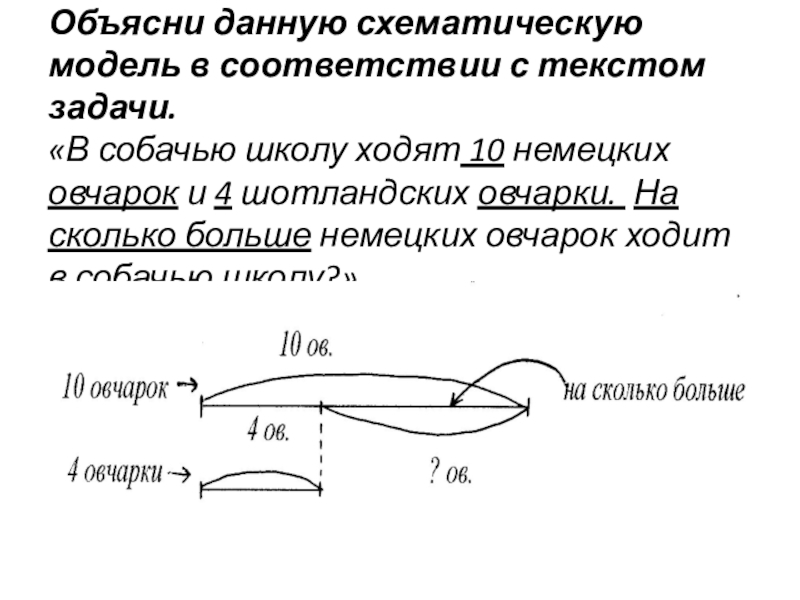
Слайд 38Объясни данную схематическую модель в соответствии с текстом задачи. «В собачью школу
ходят 10 немецких овчарок и 4 шотландских овчарки. На сколько больше немецких овчарок ходит в собачью школу?»
Слайд 40Самым важным на этом этапе является формирование умения рассуждать тем или
иным способом. Поиск плана решения задачи можно проводить двумя путями:
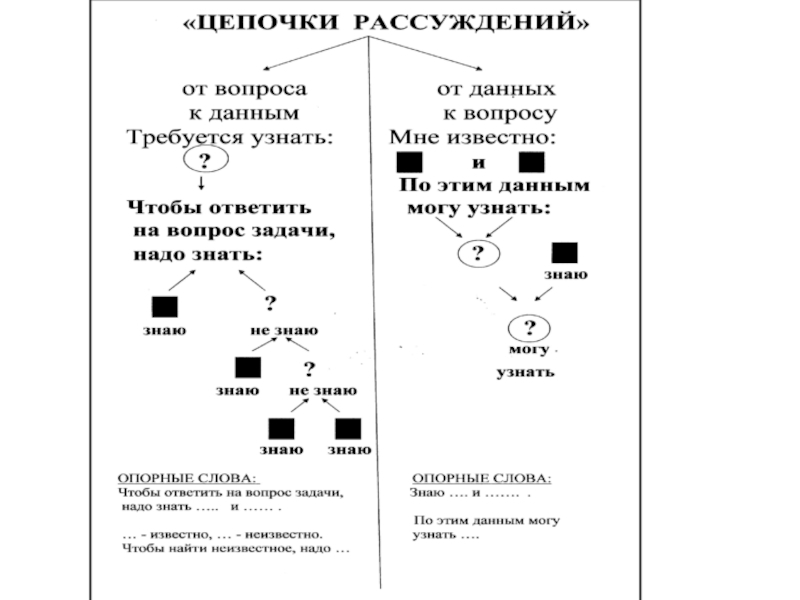
- аналитическим способом, рассуждая от вопроса к данным ( «Чтобы ответить на вопрос задачи, надо знать … и … );
- синтетическим, рассуждая от данных к вопросу.(«Мне известно … и …. По этим данным я могу узнать… и …).
Слайд 41Чаще всего применяется аналитический способ рассуждения, но с точки зрения психологии
в 1-2 классе ребёнку легче освоить синтетический способ разбора, так как в возрасте 6-8 лет формирование у ребёнка способности к синтезу несколько опережает формирование способности к анализу.
Слайд 421) Разбор от вопроса к данным ( аналитический способ)
Поиск плана решения данным способом начинается с вопроса задачи. Выясняется, что нужно узнать, чтобы ответить на вопрос задачи. Для этого необходимо найти какую-то величину. А что нужно знать, чтобы её найти? и т. д.
Слайд 43Чтобы помочь учащимся вести рассуждения аналитическим способом, можно использовать приём «ДЕРЕВО
РАССУЖДЕНИЙ». Суть его заключается в том, что по ходу рассуждений строится схема, которая помогает учащимся увидеть, какие простые задачи следует выделить (если это задача составная), и каким будет план решения данной задачи.
Слайд 44Можно оформить рассуждения в таблице. Учитель выдаёт заготовки таблицы, в которые
учащиеся записывают свои рассуждения. Такую работу целесообразно периодически проводить в 3, 4 классе.
Слайд 45 2. Разбор от данных к вопросу (синтетический)
Синтетический способ характеризуется тем, что основным, направляющим вопросом при поиске плана решения задачи является вопрос о том, что можно найти по двум или нескольким известным в задаче числовым значениям (данным). По вновь полученным числовым данным и другим известным в задаче данным вновь ищется ответ на вопрос, что можно узнать по этим значениям. И так до ответа на вопрос задачи. Суть этого способа состоит в выделении учащимися простой задачи из составной и решении её.
Слайд 46 Для формирования умения выделять простые задачи из составной, вести рассуждения
от данных можно использовать следующие упражнения:
Слайд 471) Составь и реши простые задачи, используя эти данные.
« С одной пасеки собрали 12 кг мёда, а с другой 9 кг. Весь мёд разлили в бидоне по 7 кг в каждый»
Слайд 48 2) Поставь вопрос к данному условию. Выбери только те простые
задачи, которые помогут ответить на главный вопрос.
«В школьный буфет привезли 5 ящиков яблок по 10 кг в каждом, и 4 ящика апельсинов, по 8 кг в каждом»
а) В школьный буфет привезли 5 ящиков яблок и 4 ящика апельсинов.
Сколько всего ящиков фруктов привезли в буфет?
б) В школьный буфет привезли 5 ящиков яблок по 10 кг в каждом.. Сколько кг яблок привезли?
в) В школьный буфет привезли 4 ящика апельсинов по 8 кг в каждом. Сколько кг апельсинов привезли?
Слайд 493) Использование аналогии при поиске плана решения
В основе этого способа лежит сравнение задач, при котором выявляется полное или частичное сходство отношений между данными величинами в условии ранее решённой задачи и вновь предложенной и высказывается предположение, что для решения новой задачи можно воспользоваться планом ранее решённой задачи.
Слайд 504) Поиск плана решения по модели В некоторых
случаях графическая модель подсказывает план решения задачи.
Слайд 51 « С одного поля собрали 370 т зерна, а с
другого – в два раза больше. Сколько тонн зерна собрали с двух полей?»
Данная модель показывает, для того, чтобы узнать общее количество зерна, нужно взять 3 раза по 370 тонн.
Слайд 525) Поиск плана решения путём составления уравнения
«С первого участка собрали 98 кг картофеля, со второго – 104 кг. Сколько кг картофеля собрали с третьего участка, если всего собрали 270 кг картофеля?»
- Что требуется узнать в задаче?
х кг – собрали картофеля с третьего участка
- Какие числовые данные известны в задаче?
98 кг – собрали с первого участка
104 кг – собрали со второго участка
270 кг – собрали всего с трёх участков
Слайд 55Запись решения и ответа может производиться различными способами: 1 класс – выражением
в одно действие или по действиям с пояснениями (составная задача);
2 класс - по действиям с пояснениями или вопросами;
3 класс – по действиями с пояснениями или вопросами, а также в виде числового или буквенного выражения;
4 класс – все способы + уравнением.
Слайд 56Начиная с 3-го класса, решают каждую задачу по действиям с пояснениями
или вопросами и обязательно составляют выражение. Таким образом, формирование умения записывать решение задачи с помощью выражения является более эффективным.
Слайд 58Этот этап играет большую роль в развитии самоконтроля, формировании умения рассуждать,
внимательно относиться к анализу задачи, активизирует познавательную деятельность. После анализа задачи и составления плана решения, мы выполняем прикидку ответа, то есть устанавливаем границы значений искомого с точки зрения здравого смысла.
После того, как задача решена, можно составить обратные задачи или решить задачу другими способами, если это возможно, и сравнить полученные результаты.
Слайд 60Прикидка ответа или установление границ значений искомого с точки зрения здравого
смысла (до решения).
В зоопарке было 2 зебры. Привезли ещё несколько зебр. Сколько зебр привезли, если их стало в зоопарке 7?»
- Если в зоопарке было 2 зебры, а стало 7 зебр, может получиться в ответе число большее 7? Обоснуйте свой ответ.
Слайд 61Установление соответствия между числами, полученными в результате решения задачи, и числами,
данными в условии (приём подстановки).
В зоопарке было 2 зебры. Привезли ещё несколько зебр. Сколько зебр привезли, если их стало в зоопарке 7?»
7 – 2 = 5 (з.)
- Было 2 зебры, привезли 5 зебр. Стало 7 зебр.
2 + 5 = 7 (з.)
- Сравните число, полученное при проверке с данным в задаче.
Слайд 62Составление и решение обратных задач. Этот способ вводится во 2 классе (1-4). Составить
обратную задачу – это значит преобразовать данную задачу так, чтобы искомое данной задачи стало данным числом, а одно из данных чисел – искомым.
Слайд 63Решение задачи другим способом (если это возможно в составной задаче).
Сравнение полученных результатов при решении задачи разными способами.
Слайд 65Этот этап является очень важным и интересным, хотя зачастую он опускается.
Именно работа над задачей на данном этапе способствует развитию творческой активности и мышления учащихся, повышает интерес к математике, к решению задач, позволяет целенаправленнее формировать компоненты общего умения решать задачи.
Слайд 66Приёмы работы над задачей на данном этапе: Эти приёмы также способствуют развитию
умения производить анализ задачи, устанавливать взаимосвязи между величинами, осознанно выбирать действие при решении задач.
Слайд 682) Составление аналогичной задачи с новыми данными. Этот приём помогает детям переносить
известную схему решения на другие задачи этого вида, учит обобщать их в группы.
Слайд 693) Постановка дополнительных вопросов к решённой задаче. Этот приём предполагает постановку дополнительных
вопросов, замену известных величин неизвестными, поиск новых решений. Что ещё можно узнать по имеющимся в тексте задачи и полученным данным?
Слайд 704) Изменение вопроса задачи. - Измени вопрос так, чтобы задача решалась в
одно действие, в два действия.
- Измени вопрос так, чтобы задача решалась вычитанием (делением, …).
Этот приём позволяет решить несколько задач по одному и тому же условию (при решении составных задач), тем самым экономя время, которое тратится на осмысление условия. Измени вопрос задачи так, чтобы задача решалась в два действия.
Слайд 737) Исследование решения. Сколько способов решения имеет задача? При каких условиях она
не имела бы решения? Какие приёмы целесообразны для поиска решения задачи?
Слайд 75Кроме основного вида работы над задачей – её решения, можно использовать
и другие виды работы, не включающие явное и полное решение задач, но способствующие формированию комплекса умений, необходимых для плодотворного решения задач, развитию мышления, творческой активности, познавательного интереса.
Слайд 761) Блиц-турниры Блиц-турнир предполагает устное решение простых и составных задач с
числами и с переменными (обобщённый вариант) за определённый отрезок времени, запись только решения задачи.
Слайд 783) Составление устного плана решения ( «Дерево рассуждений») и его объяснение
без последующих вычислений.
4) Разъяснение готового плана решения задачи (вопросы, «Дерево рассуждений»)
Слайд 81 «От двух пристаней, находящихся на расстоянии 510 км, отплыли Одновременно
навстречу друг другу катер и моторная лодка. Встреча произошла через 15 часов. Катер шёл со скоростью 19 км/ч. С какой скоростью шла моторная лодка?»
1способ.
1)…………. - прошёл катер до встречи
2) ………………… - проплыла моторная лодка до встречи
3) ………………… - скорость моторной лодки
2 способ.
1) …………………. - скорость сближения
2) …………………..- скорость моторной лодки
Слайд 827) Соотнесение пояснения с решением. Усложнённый вариант
– соотнесение групп пояснений с разными способами решений.
Слайд 83«Длина пришкольного участка прямоугольной формы 120 м ширина 85 м.
3 часть площади занята цветами, а остальная часть – овощами и ягодами.
Чему равна площадь участка, занятая овощами и ягодами?»
1) 120 * 85 = 10200 (кв.м ) длина участка, занятого цветами
2) 120 : 3 = 40 (м) площадь участка с цветами
3) 40 * 85 = 3400 (кв.м ) площадь участка, занятого овощами и ягодами
4) 10200 – 3400 = 6800 (кв.м ) длина участка с цветами
Слайд 848) Установление соответствия между содержанием задачи и её краткой записью (в
виде чертежа, рисунка, таблицы и т. д.) и, наоборот, между краткой записью и содержанием.
Слайд 85 9) Выбор среди нескольких схематических моделей (чертежей, таблиц, ….) той,
которая соответствует данной задаче.
10) Выбор равенства, являющегося решением задачи. Обоснование выбора.
Слайд 8611) Изменение текста задачи в соответствии с данным решением. 12) Нахождение ложного
способа решения.
Слайд 8713) Продолжение решения задачи.
«Заяц за 3 прыжка преодолел расстояние в 13 м. Первый прыжок составил 3 м, второй 5 м. Сколько метров преодолел заяц в третьем прыжке?»
1. 3 + 5 = 8(м) -……..
2.
Слайд 8814) Объяснение выражений, составленных по данному условию. «В вагоне поезда было
35 пассажиров. На станции вышли 7 пассажиров, а вошли 6.»
35 – 7 7 + 6 35 – ( 7+ 6)
35 + 6 7 - 6 35 – 7 + 6
«
Слайд 90«На турбазе 8 маленьких палаток и 5 больших. Маленькие палатки вмещают
4 человека, а большие – 10. Сколько человек может разместиться во всех этих палатках?»
Сколько всего человек вмещают маленькие палатки?______________________
Сколько всего больших и маленьких палаток на турбазе?___________________
На сколько больших палаток …, чем маленьких?___________________________
Сколько человек вмещает маленькая палатка?____________________________
Сколько всего человек вместят большие палатки?________________________
На сколько больше человек вмещают большие палатки, чем маленькие?______
Сколько всего человек вместят одна большая и маленькая палатки?_________
Слайд 9116) Составление и определение смысла всевозможных выражений ( в том числе
и не имеющих смысла в рамках данной задачи) из чисел, данных в условии задачи.
Слайд 92Этот приём трудоёмкий, но очень полезный. При его использовании учащиеся учатся
глубокому анализу числовых данных задачи, взаимосвязей между ними.
- Составь как можно больше числовых выражений с данными задачи, объясни их смысл ;
- Из числовых данных задачи и значений ранее составленных выражений составь другие выражения и объясни их смысл;
- Выбери те выражения, значения которых помогают ответить на вопрос задачи;
- Выпиши в отдельные столбцы выражения, которые имеют смысл и, которые смысла не имеют.
Слайд 9317) Составление задач: - по иллюстрации;
- по краткой записи (рисунку, чертежу, таблице, опорным
словам);
- по данной записи решения;
- по предложенной программе действий, по «Дереву
рассуждений»;
- по некоторым исходным данным: с числовыми данными 20,
25, 3;
- с определёнными условиями: в 3 действия, в ответе - 120 кг; со
словами «больше на…» и т. д.