- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Лист Мёбиуса (исследовательский проект 4 класс)
Содержание
- 1. Презентация Лист Мёбиуса (исследовательский проект 4 класс)
- 2. Творческая работаученика 4Д класса МБОУ СОШ №19
- 3. Узнать для себя что-то новое, что не
- 4. ПРОБЛЕМАЧто будет, если разрезать обычный лист бумаги?
- 5. ГИПОТЕЗА Лист Мёбиуса обладает свойствами, которых нет у кольца.
- 6. Цель: Исследование поверхности листа Мёбиуса
- 7. АВТОР Мёбиус Август Фердинанд Знаменитый
- 8. ИСТОРИЯ ОТКРЫТИЯЛист Мёбиуса относится к числу «математических
- 9. ИЗГОТОВЛЕНИЕ МОДЕЛИ Возьмём бумажную полоску в форме
- 10. ВОТ ЧТО ПОЛУЧИЛОСЬ У МЕНЯ
- 11. Исследование свойств листа МёбиусаЯ рассмотрел несколько опытов
- 12. Исследование свойств листа МёбиусаПосле этого я задался
- 13. Исследование свойств листа МёбиусаА сколько краёв имеет лист Мёбиуса?Вывод: Лист Мёбиуса имеет один край.
- 14. РАЗРЕЗАНИЕА что случится, если разрезать лист Мёбиуса
- 15. РАЗРЕЗАНИЕА если на три части? Три ленты?
- 16. РАЗРЕЗАНИЕА что получится, если разрезать на четыре
- 17. РАЗРЕЗАНИЕИтог: Получили 3 кольца, сцепленные между собой.
- 18. НЕСКОЛЬКО ПЕРЕКРУЧИВАНИЙЧтобы получить ленту, я повернул полоску
- 19. Слайд 19
- 20. ФОКУСЫ В силу своих необычных свойств лента
- 21. ФОКУСЫКак завязать на шарфе узел, не выпуская
- 22. ФОКУСЫ Как можно вывернуть наизнанку жилет,не снимая
- 23. я узнал, что существует удивительная лента ‒
- 24. Слайд 24
- 25. СПИСОК ЛИТЕРАТУРЫ 5. Гусев В.А., Орлов
- 26. СПАСИБО ЗА ВНИМАНИЕ
Слайд 2Творческая работа
ученика 4Д класса
МБОУ СОШ №19 г. Йошкар-Олы
Дербенёва Романа
Руководитель:
учитель начальных классов
Гибадуллина А. Н.
Год создания: 2015
Слайд 3Узнать для себя что-то новое,
что не изучается на уроках,
и
АКТУАЛЬНОСТЬ
Слайд 4ПРОБЛЕМА
Что будет, если разрезать обычный лист бумаги? Конечно же, два обычных
А что случится, если разрезать лист Мёбиуса вдоль посередине по всей длине? Распадётся и получится два кольца?
Слайд 6Цель:
Исследование поверхности листа Мёбиуса и его свойств
Задачи:
Узнать кто придумал такое
Изготовить модель;
Экспериментальным путём выяснить свойства листа Мёбиуса;
Показать сюрпризы этой поверхности;
Придумать математические фокусы с лентой;
Слайд 7АВТОР
Мёбиус Август Фердинанд
Знаменитый лист Мёбиуса (иногда говорят лента Мёбиуса)
Эта лента была названа в его честь лентой Мёбиуса.
Слайд 8ИСТОРИЯ ОТКРЫТИЯ
Лист Мёбиуса относится к числу «математических неожиданностей».
Рассказывают, что открыть
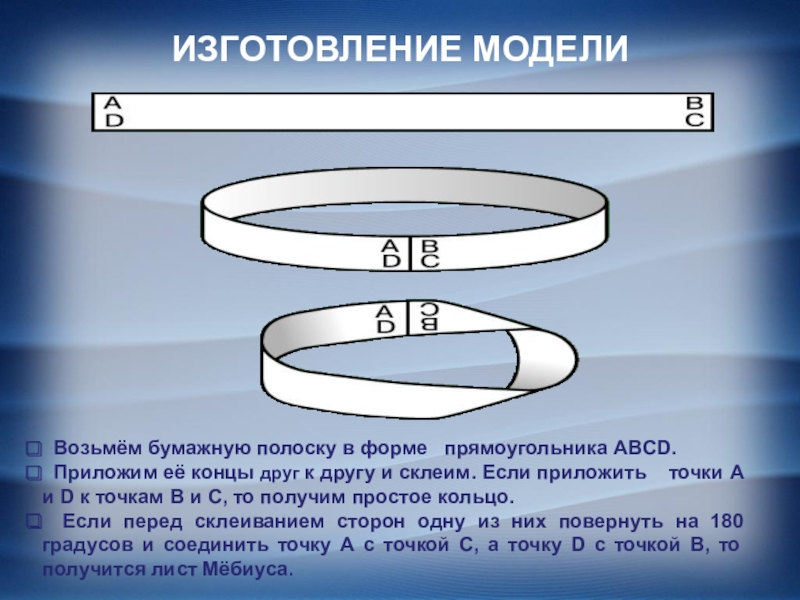
Слайд 9ИЗГОТОВЛЕНИЕ МОДЕЛИ
Возьмём бумажную полоску в форме прямоугольника ABCD.
Приложим
Если перед склеиванием сторон одну из них повернуть на 180 градусов и соединить точку А с точкой С, а точку D с точкой В, то получится лист Мёбиуса.
Слайд 11Исследование свойств листа Мёбиуса
Я рассмотрел несколько опытов с лентами, полученными из
Слайд 12Исследование свойств листа Мёбиуса
После этого я задался вопросом:
Означает ли это,
Две, как у любой другой?
Вывод: Лист Мёбиуса обладает удивительным свойством ‒ у него только одна сторона.
Слайд 13Исследование свойств листа Мёбиуса
А сколько краёв
имеет лист Мёбиуса?
Вывод: Лист Мёбиуса
Слайд 14РАЗРЕЗАНИЕ
А что случится, если разрезать лист Мёбиуса вдоль посередине по
Итог: Получили 1 кольцо, длина которого в два раза больше, ширина в два раза уже, перекручено на 1 полный оборот – «Афганская лента»
Слайд 15РАЗРЕЗАНИЕ
А если на три части? Три ленты? А ничего подобного!
Итог:
Слайд 16РАЗРЕЗАНИЕ
А что получится, если разрезать на четыре части?
Итог: получается 2 кольца
Слайд 17РАЗРЕЗАНИЕ
Итог: Получили 3 кольца, сцепленные между собой. Маленькое кольцо ‒ лист
А на пять частей?
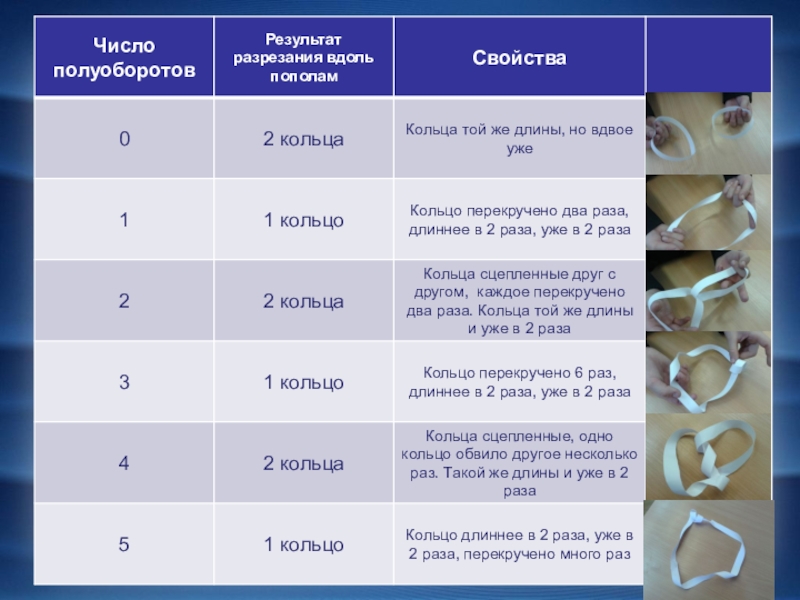
Слайд 18НЕСКОЛЬКО ПЕРЕКРУЧИВАНИЙ
Чтобы получить ленту, я повернул полоску бумаги на пол-оборота. А
Слайд 20ФОКУСЫ
В силу своих необычных свойств лента Мёбиуса широко используется
На основе исследований колец из перекрученной ленты я придумал и хочу показать серию фокусов.
Вручаем зрителю три больших бумажных кольца, каждое из которых получилось путём склеивания концов бумажной ленты. Зритель разрезает ножницами кольца вдоль ленты посередине, пока не вернётся в исходную точку. В результате из первого получится два отельных кольца. Из второго – одно кольцо, но вдвое длиннее, а из третьего – два кольца, сцепленные друг с другом.
Если трижды перекрученную ленту продеть сквозь перстень, склеить концы, а затем разрезать её вдоль посередине, то получим одно большое кольцо с узлом, завязанным вокруг перстня.
Слайд 21ФОКУСЫ
Как завязать на шарфе узел, не выпуская из рук его концов?
Это
Слайд 22ФОКУСЫ
Как можно вывернуть наизнанку жилет,
не снимая его?
Вывертывание жилета на
Слайд 23я узнал, что существует удивительная лента ‒ лист Мёбиуса;
познакомился с
научился изготавливать лист Мёбиуса и научил этому своих одноклассников;
экспериментальным путём я показал, что лист Мёбиуса является односторонней поверхностью с одним краем, что необычно для трёхмерной фигуры;
провел опыты с листом и доказал, что он изменяет свои свойства при разрезании;
увидел, что усложнение эксперимента не приводит к более эффектным результатам;
зная свойства ленты Мёбиуса, можно придумать различные фокусы и развлечения.
ВЫВОДЫ О ПРОДЕЛАННОЙ РАБОТЕ
Слайд 24
Лист Мебиуса – символ математики,
Что служит высшей мудрости венцом…
Он полон неосознанной
Здесь на глазах преобразилась плоскость
В поверхность без начала и конца.
Здесь нет пределов, нет ограничений,
Стремись вперед и открывай миры,
Почувствуй силу новых ощущений,
Прими познанья высшего дары.
Иванова Н. Ю.
Слайд 25СПИСОК ЛИТЕРАТУРЫ
5. Гусев В.А., Орлов А.И., Розенталь А.Л. Внеклассная
математике: ‒ М.: Вако, 2010
3. Стройк Д. Я. Краткий очерк истории математики : Пер. с нем. и
дополнения Погребысского И. Б. ‒ М.: Триада-Литера, 1994.
2. Лэнгдон Н., Снейп Ч. С математикой в путь: Пер. с англ. ‒ М.:
Педагогика, 1987.
1. Гарднер М. Математические чудеса и тайны: ‒ М.: Наука, 1978.
4. Шарыгин И. Ф., Еранжиева Л. Н. Наглядная геометрия: ‒ М.: Дрофа
2002.
Материалы сайтов:
http://arbuz.uz/t_lenta.html
http://www.frei.ru/golos/books/
http://umiranie.chat.ru/sphere.htm
http://school-sector.relarn.ru/dckt/projects/ctrana/matric/t_lm1.htm
http://www.kvant.info/
http://www.websib.ru/noos/math/listmebiusa/