- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Устный журнал по математике История развития тригонометрии
Содержание
- 1. Устный журнал по математике История развития тригонометрии
- 2. Тригонометрия – слово греческое и в буквальном
- 3. Наивысшими достижениями греческая тригонометрия обязана астроному Птоломею
- 4. Значительный вклад в развитие тригонометрии внесли арабские
- 5. Южно-индийские математики в 16 веке добились
- 6. Слайд 6
- 7. В 8 в ученые стран Ближнего
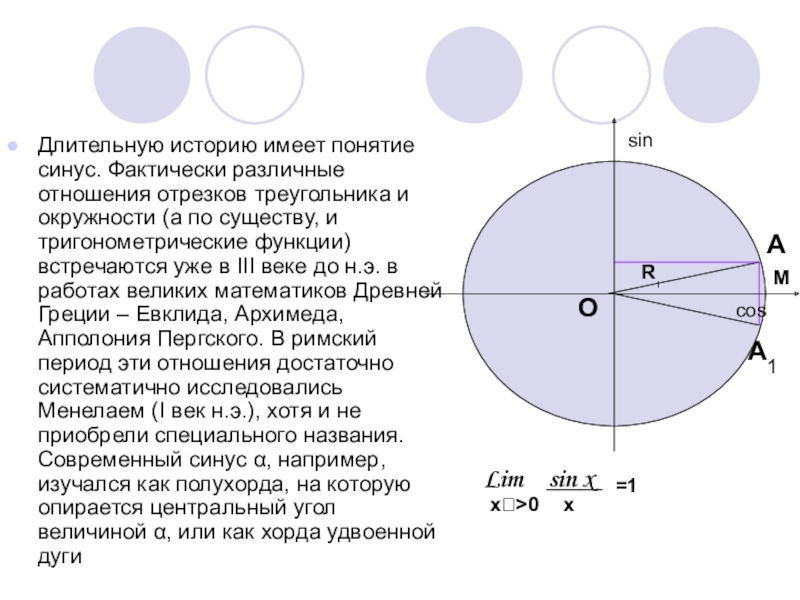
- 8. Длительную историю имеет понятие синус. Фактически различные
- 9. Слово косинус намного моложе. Косинус – это
- 10. Слайд 10
- 11. В IV-V веках появился уже специальный термин
- 12. Дальнейшее развитие тригонометрия получила в трудах выдающихся
- 13. Аналитическая теория тригонометрических функций в основном была
- 14. Пожалуй, наибольшие стимулы к развитию тригонометрии возникали
Слайд 2Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников
Слайд 3Наивысшими достижениями греческая тригонометрия обязана астроному Птоломею (2 век н.э.), создателю
Слайд 4Значительный вклад в развитие тригонометрии внесли арабские ученые Аль-Батани (850-929) и
Слайд 5 Южно-индийские математики в 16 веке добились больших успехов в области
А в анонимном трактате «Каранападдхати»(«Техника вычислений») даны правила разложения синуса и косинуса в бесконечные степенные ряды. Нужно сказать, что в Европе к подобным результатам подошли лишь в 17-18 веках. Так, ряды для синуса и косинуса вывел И.Ньютон около 1666 г., а ряд арктангенса был найден Дж Грегори в 1671 г. и Г.В.Лейбницем в 1673 г.
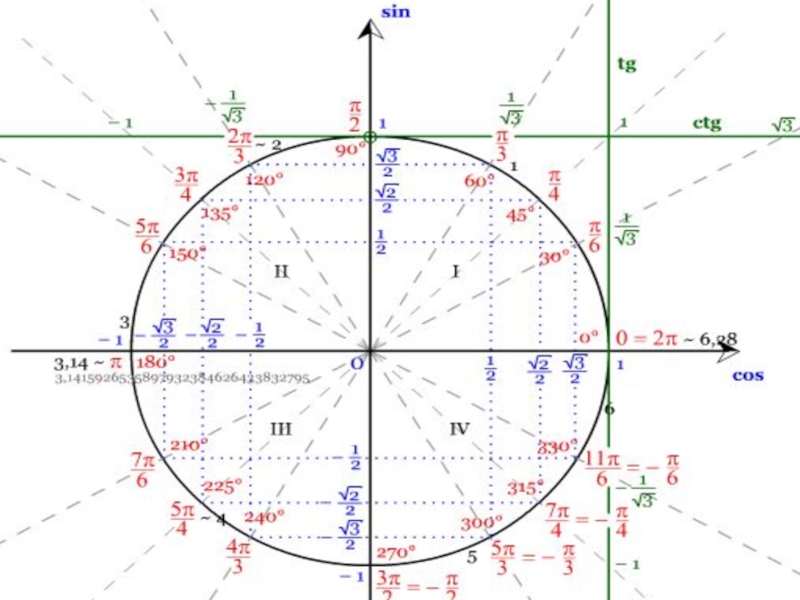
Слайд 6
sin a + cos a = 1,
sin a = cos (90° - a)
sin (a + B)= sin a * cos B + cos a * sin B.
2 2
Значительные высоты достигла тригонометрия и у индийских средневековых астрономов. Главным достижением индийских астрономов стала замена хорд синусами, что позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом в Индии было положено начало тригонометрии как учению о тригонометрических величинах.
Индийские ученые пользовались различными тригонометрическими соотношениями, в том числе и теми, которые в современной форме выражается как
Слайд 7 В 8 в ученые стран Ближнего и Среднего Востока познакомились
Слайд 8Длительную историю имеет понятие синус. Фактически различные отношения отрезков треугольника и
А
1
А
О
М
R
sin
cos
Lim sin x
_____
x
x>0
=1
Слайд 9
Слово косинус намного моложе. Косинус – это сокращение латинского выражения completely
Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь в XIV веке немецким математиком, астрономом Регимонтаном (1467 г.).
Слайд 11В IV-V веках появился уже специальный термин в трудах по астрономии
Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus – изгиб, кривизна).
Слайд 12Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543)
Слайд 13Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII
Слайд 14Пожалуй, наибольшие стимулы к развитию тригонометрии возникали в связи с решением
Начиная с XVII в., тригонометрические
функции начали применять
к решению уравнений,
задач механики, оптики,
электричества, радиотехники,