- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проект Графики в нашей жизни
Содержание
- 1. Проект Графики в нашей жизни
- 2. ГипотезаЯ предполагаю, что графики - неотъемлемая часть нашей жизни.
- 3. Цель:Выяснить, действительно ли нас повсюду окружают графики.
- 4. Задачи:Узнать историю происхождения графиков.Найти и рассмотреть графики,
- 5. Откуда к нам пришли графики?
- 6. Возникновение и понятие функции в Древнем ЕгиптеКогда
- 7. Возникновение и понятие функции в Древнем ВавилонеВысокого
- 8. Возникновение и понятие функции в Древней Греции В
- 9. Рене ДекартДекарт пришел к идеям о единстве
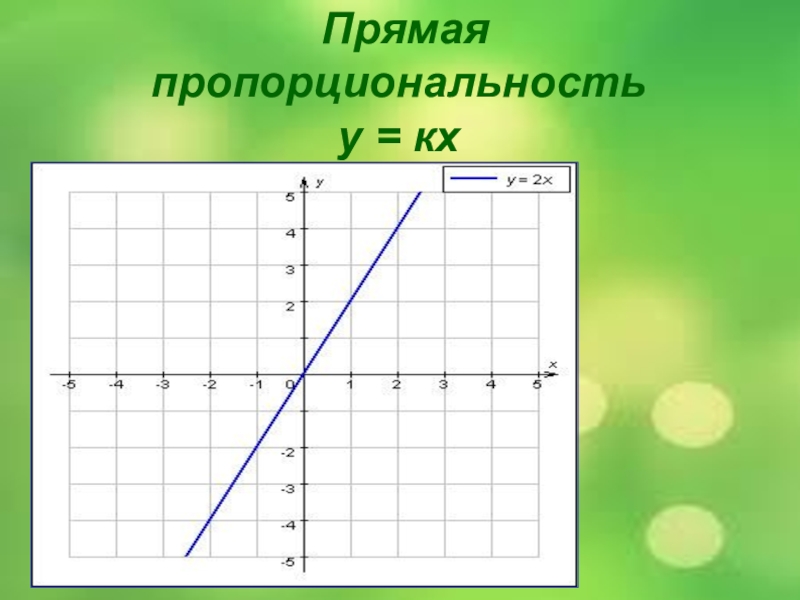
- 10. Прямая пропорциональность у = кх
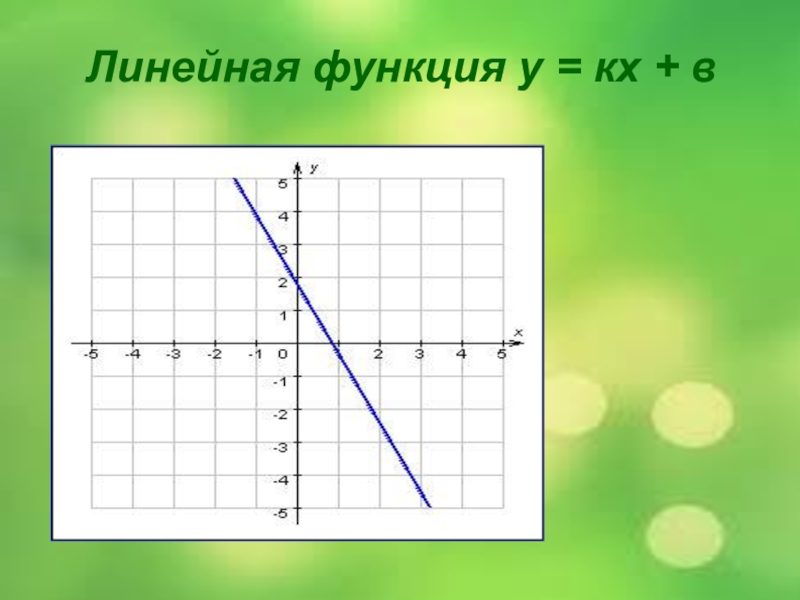
- 11. Линейная функция у = кх + в
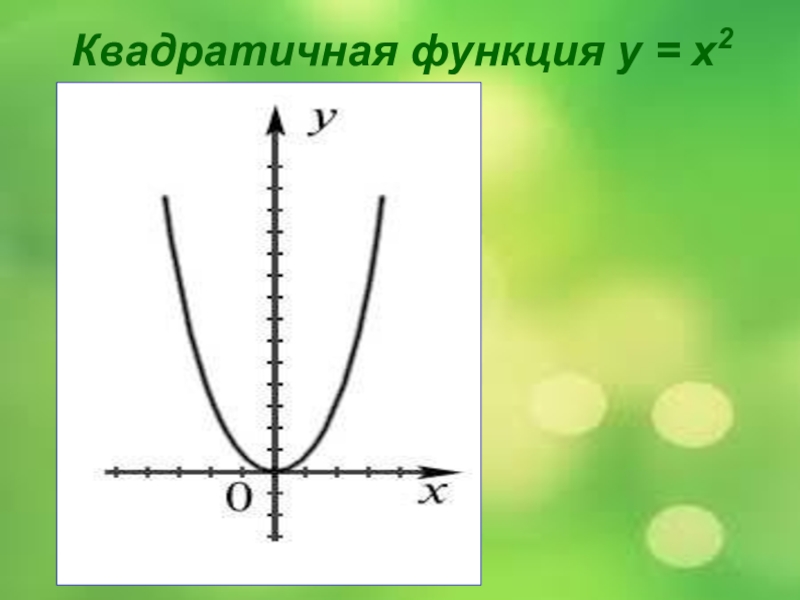
- 12. Квадратичная функция у = х2
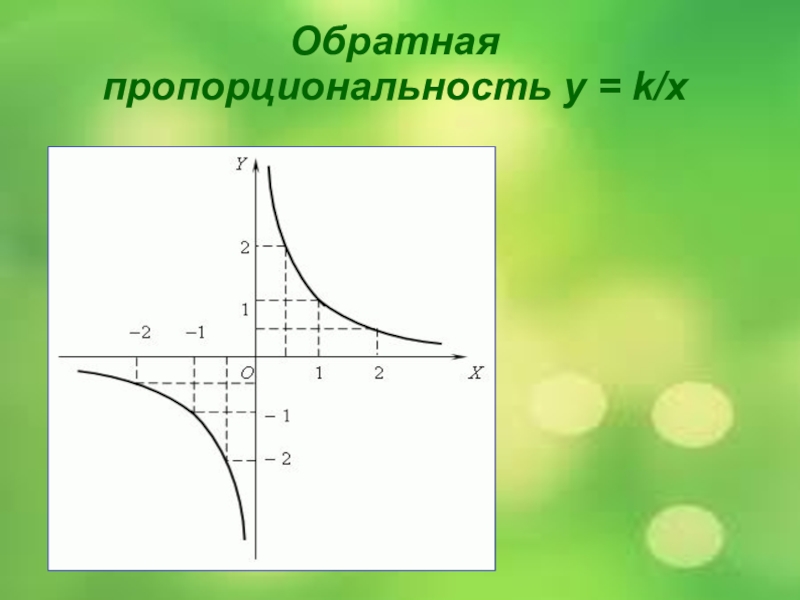
- 13. Обратная пропорциональность у = k/x
- 14. Синусоида
- 15. Графики в реальной жизниЯблоко растёт, затем его срывают и сушат.( х – время;у – масса яблока)
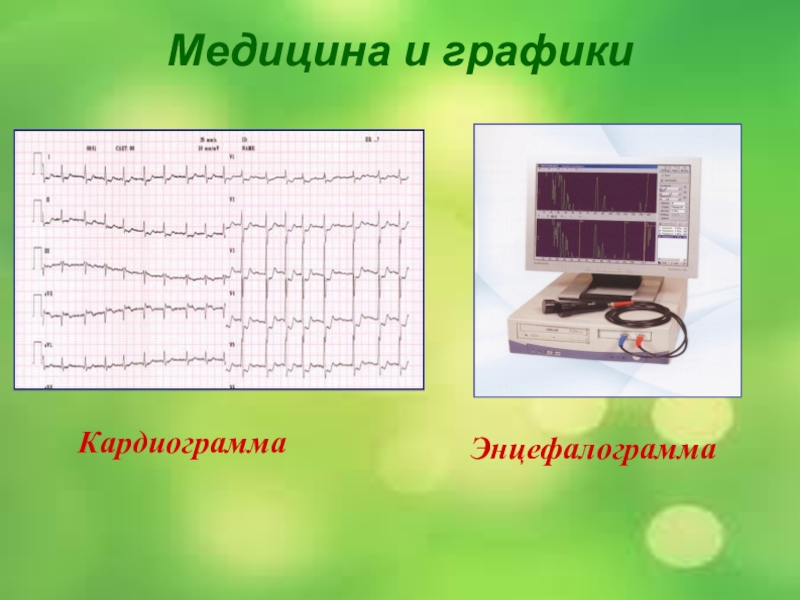
- 16. Медицина и графикиКардиограммаЭнцефалограмма
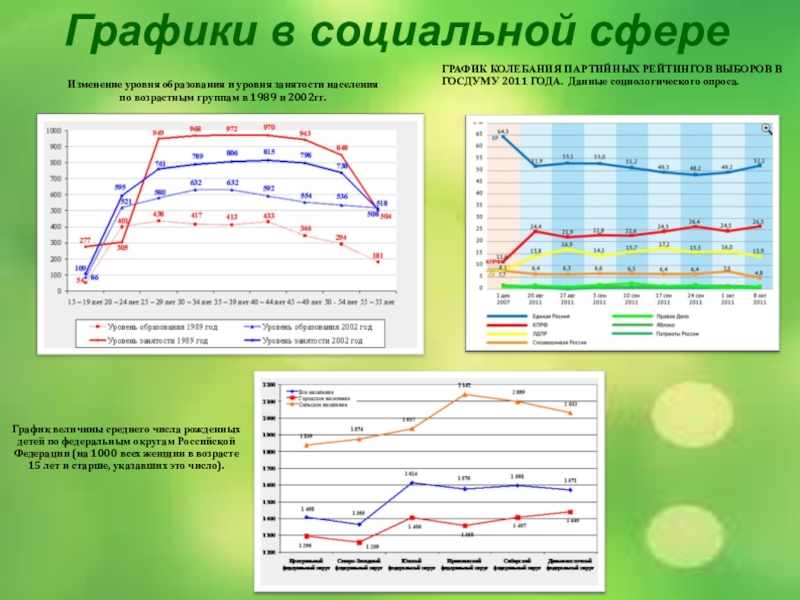
- 17. Графики в социальной сфереГРАФИК КОЛЕБАНИЯ ПАРТИЙНЫХ РЕЙТИНГОВ
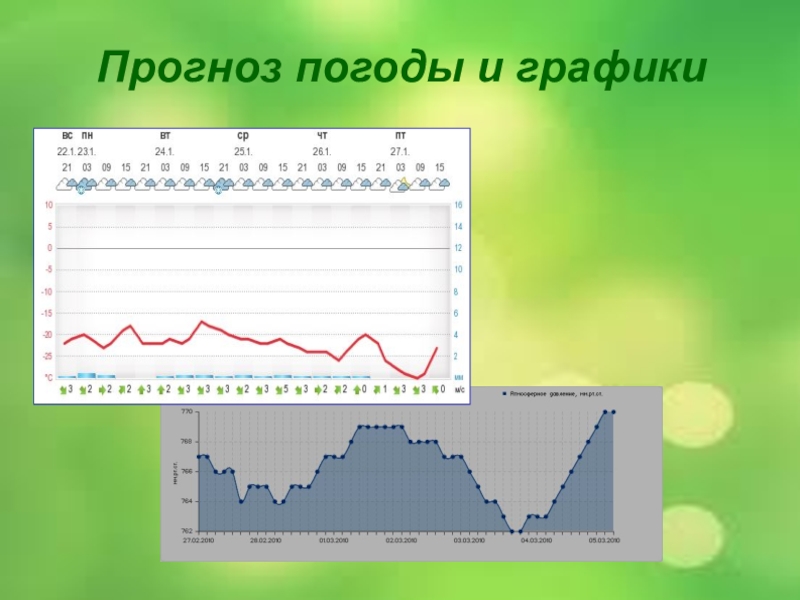
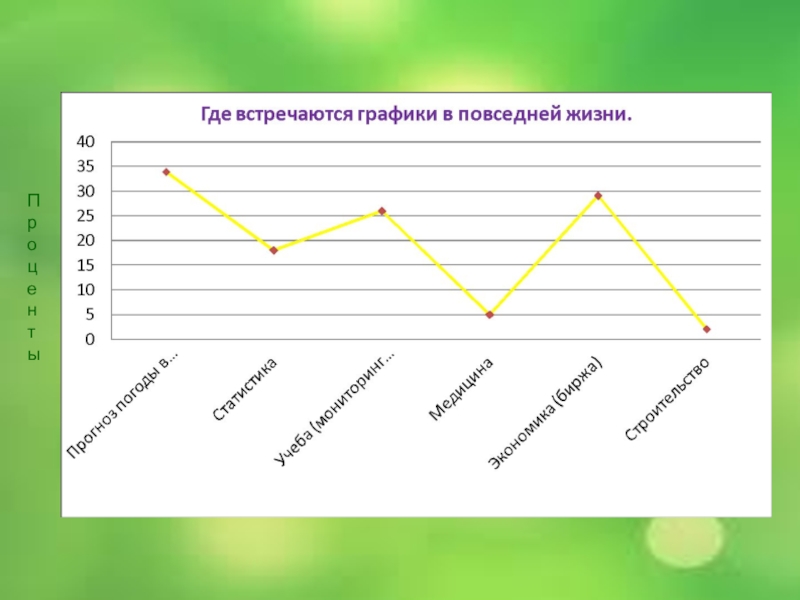
- 18. Прогноз погоды и графики
- 19. Закон экологического оптимумаВлияние температуры на скорость роста
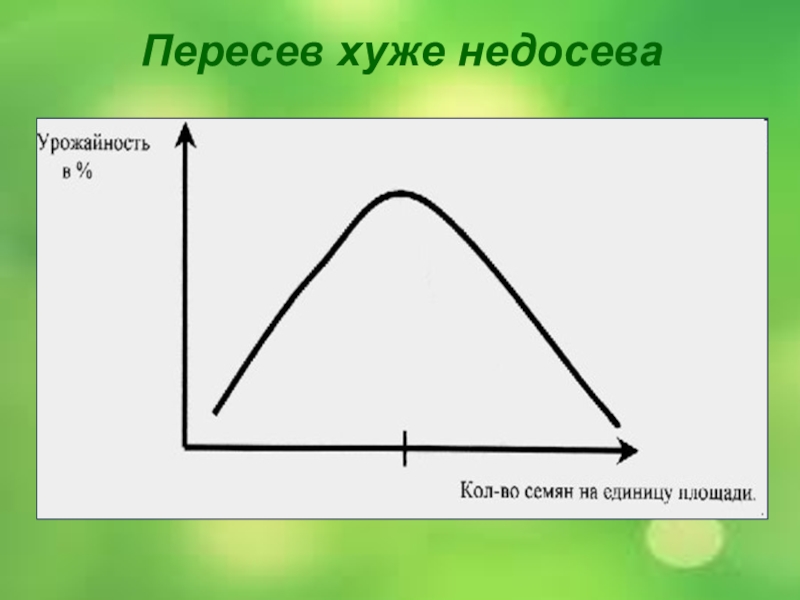
- 20. Пересев хуже недосева
- 21. Проценты
- 22. Опрос № 2: «Что мешает нам хорошо учиться?» Выявление причин, вызывающих усталость от учёбы в школе
- 23. Слайд 23
- 24. Построим таблицу значений:При 0 < Х <
- 25. Слайд 25
- 26. Слайд 26
- 27. Подставляем значения Т в формулу:
- 28. Слайд 28
- 29. Слайд 29
- 30. Будем находить
- 31. Слайд 31
- 32. С помощью графиков функций можно рисовать картины,
- 33. В изобразительном искусстве есть еще одно направление
- 34. Контур головы птицы лучше всего нарисовать с
- 35. 25. y= 2(x-3,5)2+10 для х€ [3;3,5] 26.
- 36. 4. Вывод: выяснили, что люди в жизни
- 37. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 4Задачи:
Узнать историю происхождения графиков.
Найти и рассмотреть графики, которые окружают нас в
3) Выяснить, как часто люди в жизни встречаются с графиками.
Слайд 6Возникновение и понятие функции в Древнем Египте
Когда возникли ᴨервые цивилизации, образовались
Слайд 7Возникновение
и понятие
функции в
Древнем Вавилоне
Высокого уровня достигла математика в
Пользуясь такими таблицами, вавилоняне могли решать и обратные задачи - по заданному объему куба находить длину его стороны, т.е. Извлекать кубические корни. Они умели даже решать уравнения вида x2 + x3 = a. Были у вавилонян и таблицы функций двух переменных, например таблицы сложения и умножения. Пользуясь различными таблицами, они могли вычислить и длину гипотенузы по длинам катетов, т.е. Находить значение функции
Разумеется, путь от появления таблиц до создания общего понятия функциональной зависимости был еще очень долог, но первые шаги по этому пути уже были сделаны.
Слайд 8Возникновение и понятие функции в Древней Греции
В Древней Греции наука приняла
Слайд 9Рене Декарт
Декарт пришел к идеям о единстве алгебры и геометрии и
Слайд 15Графики в реальной жизни
Яблоко растёт, затем его срывают и сушат.
( х
у – масса яблока)
Слайд 17Графики в социальной сфере
ГРАФИК КОЛЕБАНИЯ ПАРТИЙНЫХ РЕЙТИНГОВ ВЫБОРОВ В ГОСДУМУ 2011
График величины среднего числа рожденных детей по федеральным округам Российской Федерации (на 1000 всех женщин в возрасте 15 лет и старше, указавших это число).
Изменение уровня образования и уровня занятости населения
по возрастным группам в 1989 и 2002гг.
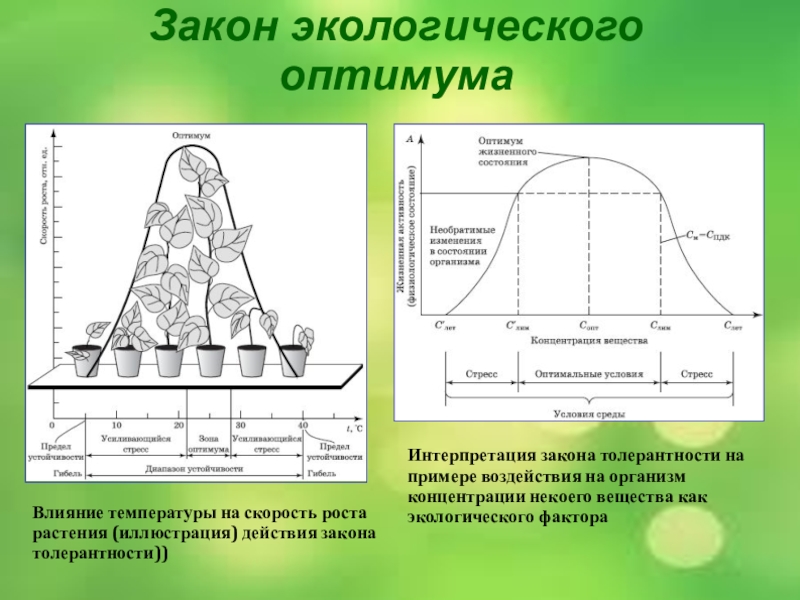
Слайд 19Закон экологического оптимума
Влияние температуры на скорость роста растения (иллюстрация) действия закона
Интерпретация закона толерантности на примере воздействия на организм концентрации некоего вещества как экологического фактора
Слайд 22 Опрос № 2: «Что мешает нам хорошо учиться?» Выявление причин, вызывающих усталость
Слайд 23
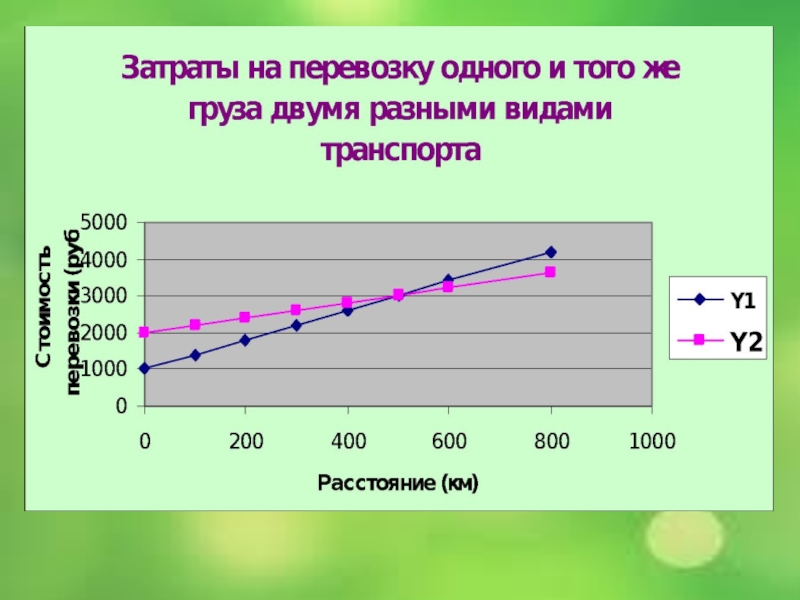
Затраты на перевозку одного и того же груза двумя разными видами транспорта определяются формулами:
У1 = 1000 + 4х,
У2 = 2000 + 2х,
Где х – расстояние в километрах,
У1 ,У2 – стоимость перевозки в рублях.
Постройте графики этих функций. При каких значениях х выгоднее пользоваться первым видом транспорта? Начиная с какого расстояния экономичнее становится второй вид транспорта?
Слайд 24Построим
таблицу значений:
При 0 < Х < 500 км, выгоднее пользоваться
Начиная с расстояния в 500 км. экономичнее становится второй вид транспорта.
Слайд 26
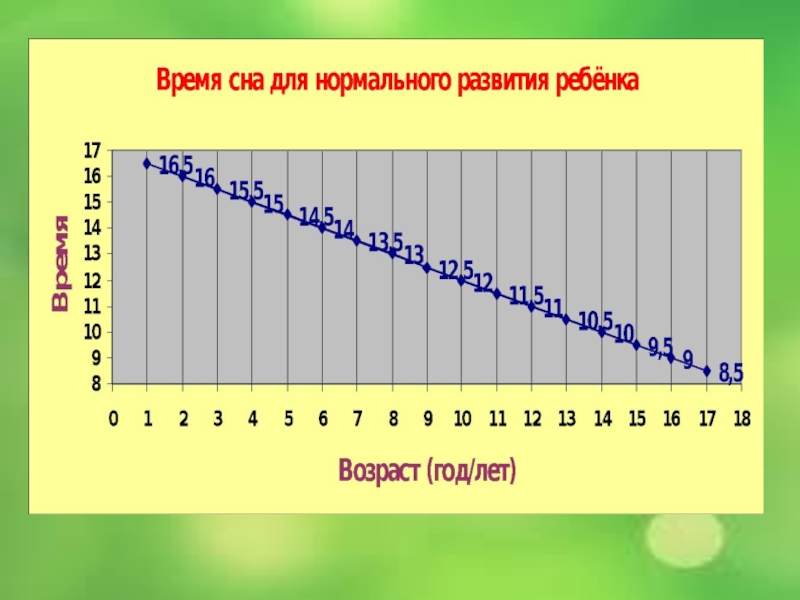
Медиками установлено, что для нормального развития ребенок или подросток, которому Т лет (Т меньше 18), должен спать в сутки t часов, где t определяется по формуле t = 17 – Т/2.
Найдите Т(2); Т(13) ; Т(16).
Слайд 27Подставляем значения Т в формулу:
Если ребёнку
2 года: 13 лет: 16 лет:
t = 17 – 2:2 t = 17 – 13:2 t = 17 – 16:2
t = 16 ч. t = 17- 6,5 t = 17 - 8
t = 10,5 ч. t = 9 ч.
Баю – баюшки,
баю …
Слайд 29
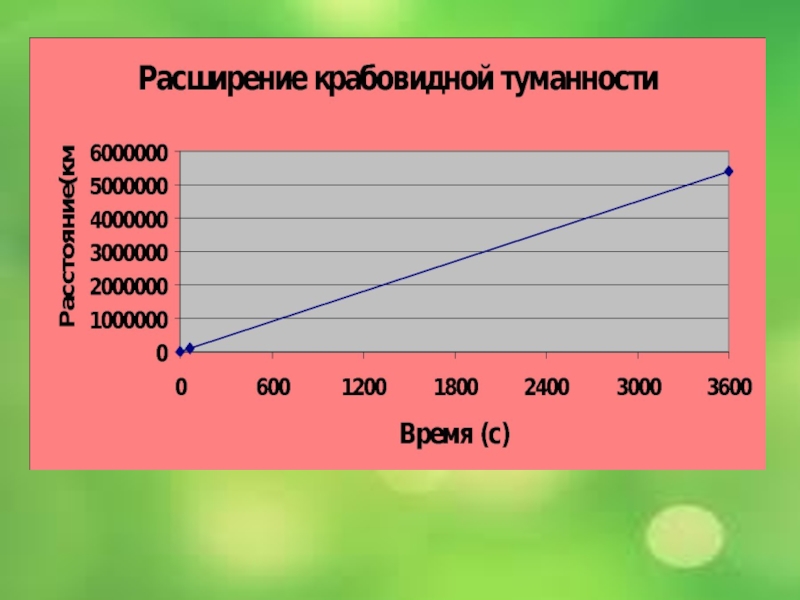
Крабовидная туманность в созвездии Тельца расширяется со скоростью 1500 км/с. На какое расстояние расширяется туманность за минуту, за час? Постройте график.
Решение задачи.
Слайд 30 Будем находить по формуле
Подставляя значения в формулу, получим:
S=1500 км/с*60 с =90000 км - за минуту
S=1500 км/с*3600с = 5400000 км – за час
Слайд 32С помощью графиков функций можно рисовать картины, рисунки выполненные в стиле
Слайд 33В изобразительном искусстве есть еще одно направление изобразительного искусства, появившегося в
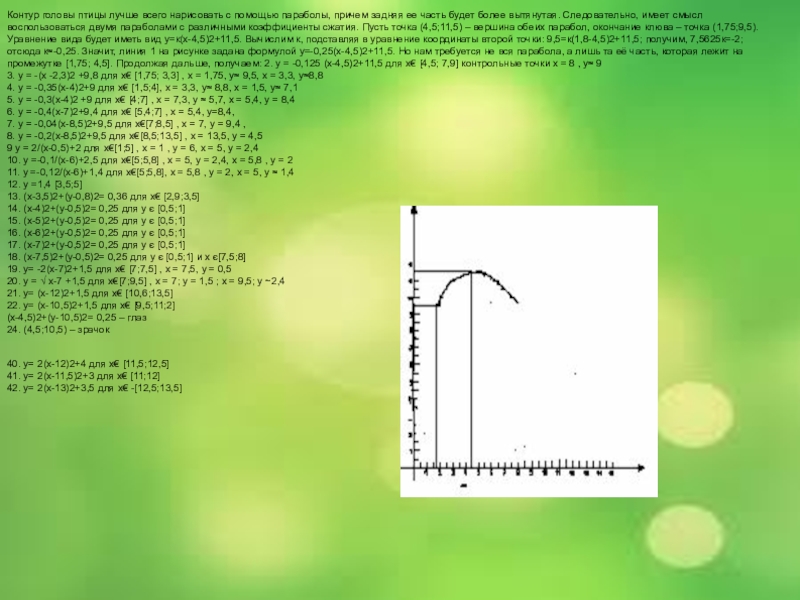
Слайд 34Контур головы птицы лучше всего нарисовать с помощью параболы, причем задняя
3. у = -(x -2,3)2 +9,8 для х€ [1,75; 3,3] , x = 1,75, y≈ 9,5, x = 3,3, y≈8,8
4. y = -0,35(x-4)2+9 для х€ [1,5;4], x = 3,3, y≈ 8,8, x = 1,5, y≈ 7,1
5. y = -0,3(x-4)2 +9 для х€ [4;7] , x = 7,3, y ≈ 5,7, x = 5,4, y = 8,4
6. y = -0,4(x-7)2+9,4 для х€ [5,4;7] , x = 5,4, y=8,4,
7. y = -0,04(x-8,5)2+9,5 для х€[7;8,5] , x = 7, y = 9,4 ,
8. y = -0,2(x-8,5)2+9,5 для х€[8,5;13,5] , x = 13,5, y = 4,5
9 y = 2/(х-0,5)+2 для х€[1;5] , x = 1 , y = 6, x = 5, y = 2,4
10. y =-0,1/(х-6)+2,5 для х€[5;5,8] , x = 5, y = 2,4, x = 5,8 , y = 2
11. y =-0,12/(х-6)+1,4 для х€[5;5,8], x = 5,8 , y = 2, x = 5, y ≈ 1,4
12. y =1,4 [3,5;5]
13. (x-3,5)2+(y-0,8)2= 0,36 для х€ [2,9;3,5]
14. (x-4)2+(y-0,5)2= 0,25 для y є [0,5;1]
15. (x-5)2+(y-0,5)2= 0,25 для y є [0,5;1]
16. (x-6)2+(y-0,5)2= 0,25 для y є [0,5;1]
17. (x-7)2+(y-0,5)2= 0,25 для y є [0,5;1]
18. (x-7,5)2+(y-0,5)2= 0,25 для y є [0,5;1] и х є[7,5;8]
19. y= -2(x-7)2+1,5 для х€ [7;7,5] , x = 7,5, y = 0,5
20. y = √ x-7 +1,5 для х€[7;9,5] , x = 7; y = 1,5 ; x = 9,5; y ~2,4
21. y= (x-12)2+1,5 для х€ [10,6;13,5]
22. y= (x-10,5)2+1,5 для х€ [9,5;11;2]
(x-4,5)2+(y-10,5)2= 0,25 – глаз
24. (4,5;10,5) – зрачок
40. y= 2(x-12)2+4 для х€ [11,5;12,5]
41. y= 2(x-11,5)2+3 для х€ [11;12]
42. y= 2(x-13)2+3,5 для х€ -[12,5;13,5]
Слайд 3525. y= 2(x-3,5)2+10 для х€ [3;3,5]
26. y= -2(x-3,5)2+10 для х€
27. y= 2(x-8)2+7,5 для х€ [7,5;8,5]
28. y= 2(x-10)2+7,5 для х€ [9,5;10,5]
29. y= 2(x-9)2+6,5 для х€ [8,5;9,5]
30. y= 2(x-11)2+6,5 для х€ [10,5;11,5]
31. y= 2(x-12,5)2+6,5 для х€ [12;13]
32. y= 2(x-8)2+6 для х€ [7,5;8,5]
33. y= 2(x-10)2+5,5 для х€ [9,5;10,5]
y= 2(x-11,5)2+5,5 [11;12]
35. y= 2(x-9)2+5 для х€ [8,59,5]
36. y= 2(x-12,5)2+5 для х€ [12;13]
37. y= 2(x-8)2+4,5 для х€ [7,5;8,5]
38. y= 2(x-11)2+4,5 для х€ [10,5;11,5]
39. y= 2(x-9,5)2+4 для х€ [9;10]
40. y= 2(x-12)2+4 для х€ [11,5;12,5]
41. y= 2(x-11,5)2+3 для х€ [11;12]
42. y= 2(x-13)2+3,5 для х€ -[12,5;13,5]
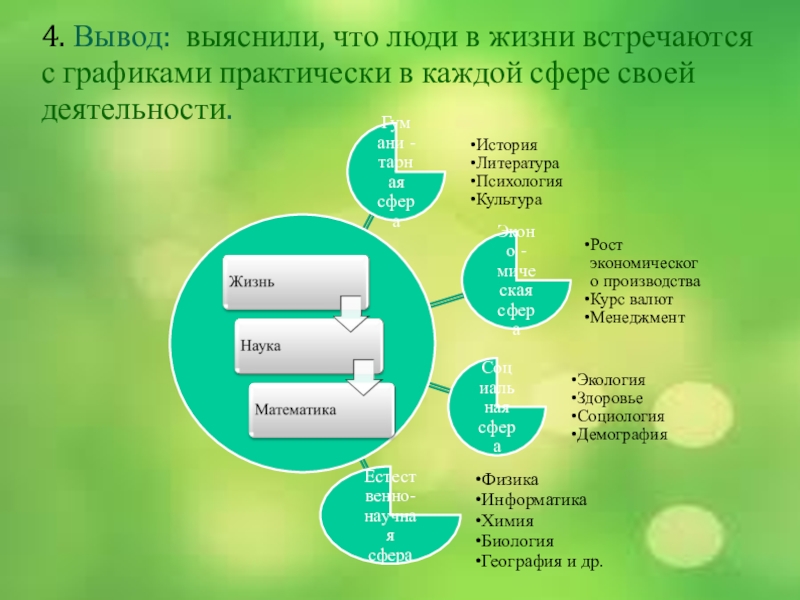
Слайд 364. Вывод: выяснили, что люди в жизни встречаются с графиками практически
Гумани -тарная сфера
История
Литература
Психология
Культура
Эконо -мическая сфера
Рост экономического производства
Курс валют
Менеджмент
Социальная сфера
Экология
Здоровье
Социология
Демография
Естественно-научная сфера
Физика
Информатика
Химия
Биология
География и др.




















![Проект Графики в нашей жизни 25. y= 2(x-3,5)2+10 для х€ [3;3,5] 26. y= -2(x-3,5)2+10 для х€ 25. y= 2(x-3,5)2+10 для х€ [3;3,5] 26. y= -2(x-3,5)2+10 для х€ [3;3,5] 27. y= 2(x-8)2+7,5 для х€](/img/thumbs/7d0d014a915ba2fefd4be593a9754733-800x.jpg)