- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Алгебраические выражения
Содержание
- 1. Презентация по теме Алгебраические выражения
- 2. Множества, элементами которых являются числа, называются числовыми.
- 3. Понятие выраженияЧисловое выражение – это любая запись
- 4. Виды алгебраических выражений.Рациональные алгебраические выражения – это
- 5. Область определения алгебраического выражения. Множество значений
- 6. Приведение подобных слагаемыхПодобные слагаемые — это слагаемые, которые имеют одинаковую буквенную часть.
- 7. Раскройте скобки и приведите подобные слагаемые:
- 8. Тождество – это равенство, справедливое при всех
- 9. Являются ли тождественно равными выражения:а) (2а)(7b) и
- 10. Слайд 10
- 11. Представьте выражение в виде многочлена стандартного видаа)
- 12. Степень с целым показателем и ее свойства
- 13. Свойства степени с целым показателем
- 14. Вычислить
- 15. Слайд 15
- 16. Применение свойств степени к решению примеров1.Сократить дробь:2. Упростить выражения: 3*. Сократить дробь:
- 17. Стандартный вид числаСтандартный вид (экспоненциальная форма) числа
- 18. Выполнить действия с числами в стандартном виде и записать ответ в стандартном виде.
- 19. Площадь территории России составляет 17,1 млн км2.
- 20. Формулы сокращенного умножения
- 21. Формулы для квадратов(a + b)2 = a2
- 22. Формулы для кубов(a + b)3 = a3
- 23. Преобразовать, используя формулы сокращенного умножения
- 24. Разложение многочленов на множители Тождественное преобразование,
- 25. Теорема о разложении квадратного трехчленаРазложить на множители квадратный трехчлен:
- 26. Разложите на множители
- 27. Преобразовать выражения
- 28. Действия с алгебраическими дробями
- 29. Сократить дробь
- 30. Выполнить действия
- 31. Понятие квадратного корня и его свойства.
- 32. Квадратные корни
- 33. Слайд 33
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. Слайд 37
Слайд 1Автор: Зеленская О.Ю.
ДовДополнительная образовательная программа
«Подготовительный курс для абитуриентов колледжа» по
Тема: Понятие алгебраического выражения. Преобразование выражений. по Математике
Слайд 2
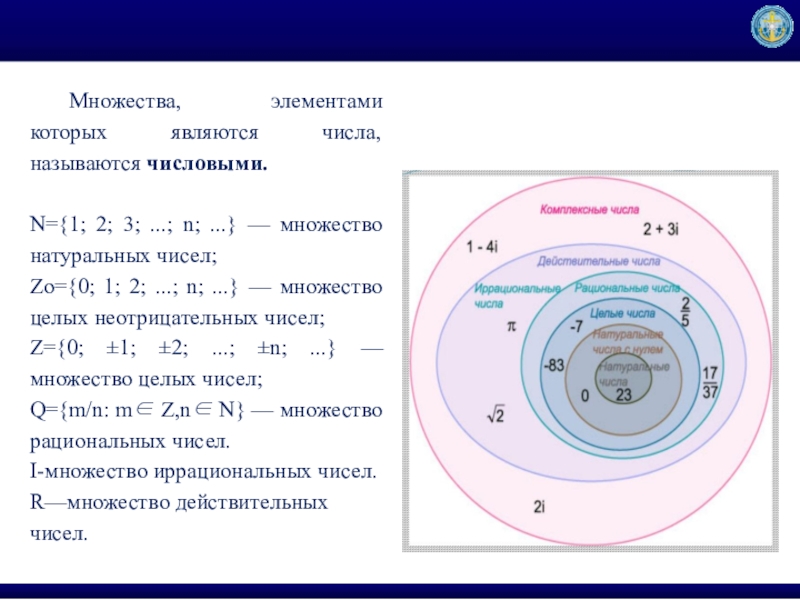
Множества, элементами которых являются числа, называются числовыми.
N={1; 2; 3; ...;
Zo={0; 1; 2; ...; n; ...} — множество целых неотрицательных чисел;
Z={0; ±1; ±2; ...; ±n; ...} — множество целых чисел;
Q={m/n: m∈ Z,n∈ N} — множество рациональных чисел.
I-множество иррациональных чисел.
R—множество действительных чисел.
Слайд 3Понятие выражения
Числовое выражение – это любая запись из чисел, знаков арифметических
Выражение, содержащее буквы, которыми обозначены некоторые числа, называется буквенным выражением.
Алгебраическим выражением называется одна или несколько алгебраических величин (чисел и букв), соединенных между собой знаками алгебраических действий: сложения, вычитания, умножения и деления, а также извлечения корня и возведения в целую степень и знаками последовательности этих действий (обычно скобками различного вида).
Слайд 4Виды алгебраических выражений.
Рациональные алгебраические выражения – это целые и дробные алгебраические
Целое алгебраическое выражение.В целых алгебраических выражениях все значения переменных являются допустимыми.
Дробное. В дробных алгебраических выражениях допустимыми являются все значения переменных, при которых не происходит деления на нуль.
II. Иррациональные алгебраические выражения содержат извлечение корня из переменной или возведение переменной в дробную степень.
Слайд 5Область определения алгебраического выражения.
Множество значений переменной, при которых выражение
Также можно сказать, что область определения выражения – это множество всех допустимых значений переменной.
Найти ОДЗ выражения:
Слайд 6Приведение подобных слагаемых
Подобные слагаемые — это слагаемые, которые имеют одинаковую буквенную
Слайд 8
Тождество – это равенство, справедливое при всех допустимых значениях входящих в
Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения.
Слайд 9
Являются ли тождественно равными выражения:
а) (2а)(7b) и 14аb;
б) -2а + 2а
в) х - у и у - х;
г) (х - у)² и (у - х)².
Являются ли тождественно равными выражения:
а) 2 + 8bа и 8аb + 2;
б) 2х + 7 и 2(x + 7);
в) (а + b) • 0 и а + b;
г) (а + b) • 2 и 2а + 2b.
Слайд 11Представьте выражение в виде многочлена стандартного вида
а) 3(6 - 5x) +
б) 8(3у + 4) - 29у + 14;
в) 7(2z - 3) + 6z - 12;
г) 2(7,3 - 1,6а) + 3,2а - 9,6;
д) -5(0,Зb + 1,7) + 12,5 - 8,5b;
е) -4(3,3 - 8с) + 4,8с + 5,2.
Слайд 16Применение свойств степени к решению примеров
1.Сократить дробь:
2. Упростить выражения:
3*. Сократить
Слайд 17Стандартный вид числа
Стандартный вид (экспоненциальная форма) числа — запись числа в
где n – целое число, 1 ≤ a < 10
а - называют мантиссой числа, n - порядком числа.
Например:
2170000 = 2,17×106
0,00000267 = 2,67 × 10-6
Каждое число, бóльшее 10, можно записать в стандартном виде:
a · 10n, где 1 ≤ a ≤ 10 и n — натуральное число.
Слайд 19
Площадь территории России составляет 17,1 млн км2. Как эта величина записывается
Расстояние от Юпитера — одной из планет Солнечной системы — до Солнца равно 778,1 млн км. Как эта величина записывается в стандартном виде?
Площадь поверхности Плутона — одной из планет Солнечной системы — равна 17,95 млн. км2. Как эта величина записывается в стандартном виде?
Число молекул газа в 1 см3 при 0°С и давлении 760 мм.рс.ст равно 27 000 000 000 000 000 000. Записать это число в стандартном виде.
Слайд 21Формулы для квадратов
(a + b)2 = a2 + 2ab + b2–
(a – b)2 = a2 – 2ab + b2– квадрат разности двух чисел
a2 – b2 = (a – b)(a + b) – разность квадратов
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc – квадрат суммы трех чисел
Слайд 22Формулы для кубов
(a + b)3 = a3 + 3a2b + 3ab2
(a – b)3 = a3 – 3a2b + 3ab2 – b3– куб разности
a3 + b3 = (a + b)(a2 – ab + b2)– сумма кубов
a3 – b3 = (a – b)(a2 + ab + b2)– разность кубов
Слайд 24Разложение многочленов на множители
Тождественное преобразование, приводящее к произведению нескольких
Основные методы разложения на множители:
Вынесение общего множителя за скобки.
Использование формул сокращенного умножения.
Способ группировки.
Способ выделения полного квадрата.