- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Производная, 10 класс
Содержание
- 1. Презентация по математике Производная, 10 класс
- 2. 1:: Find the derivative of polynomials.2:: Find
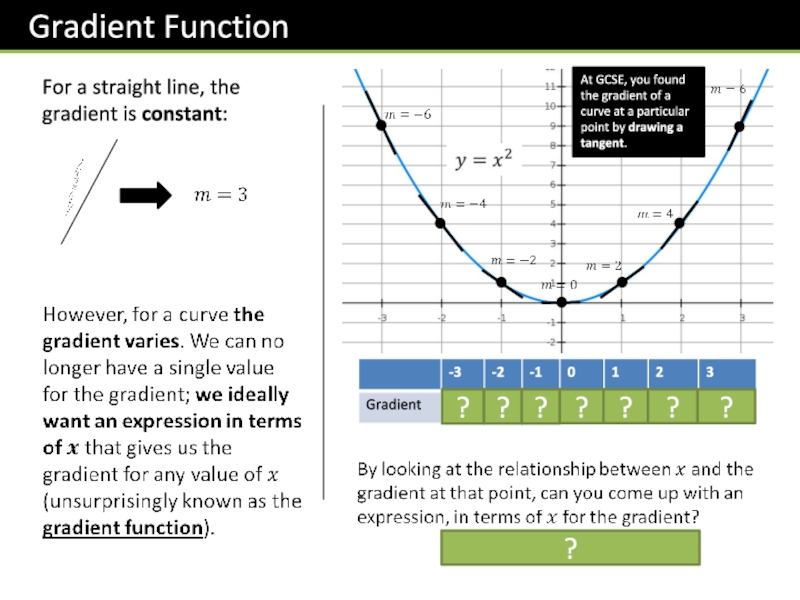
- 3. For a straight line, the gradient is
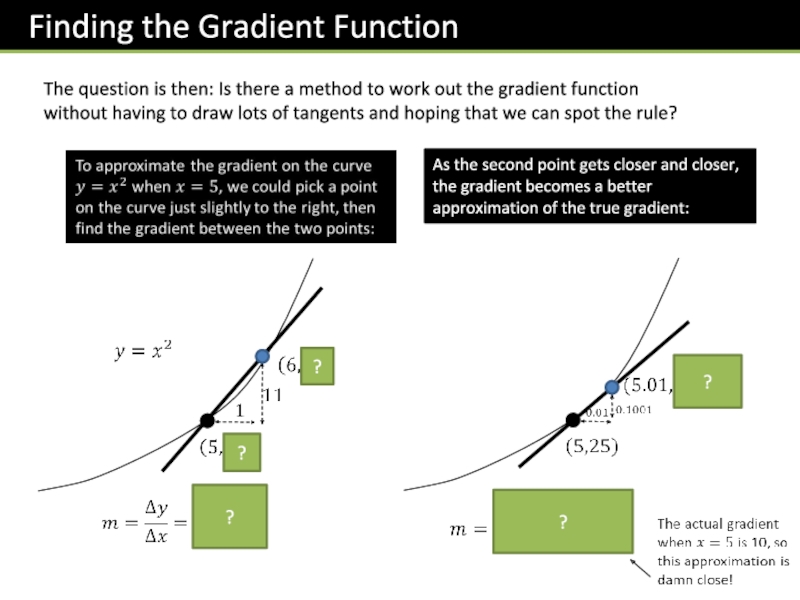
- 4. The question is then: Is there a
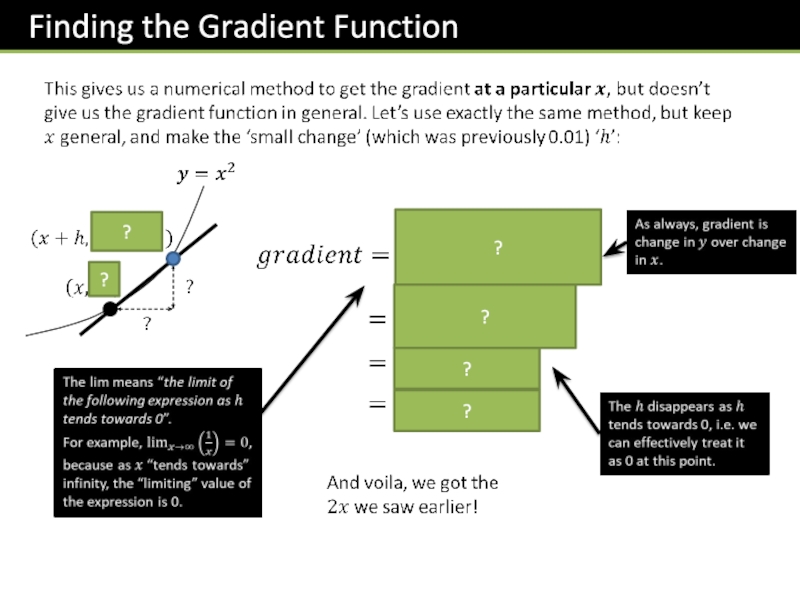
- 5. ??????
- 6. “Lagrange’s notation”“Leibniz’s notation”
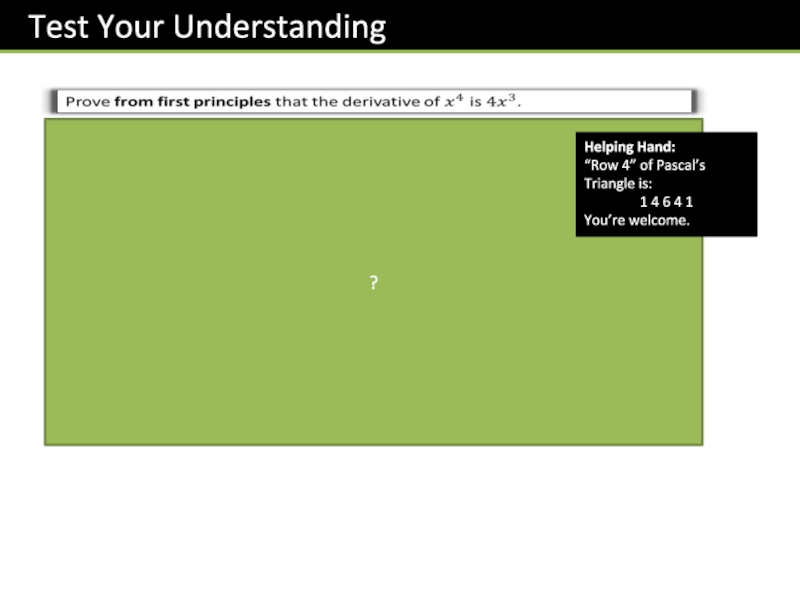
- 7. !Use the “differentiation by first principles” formula.ab??
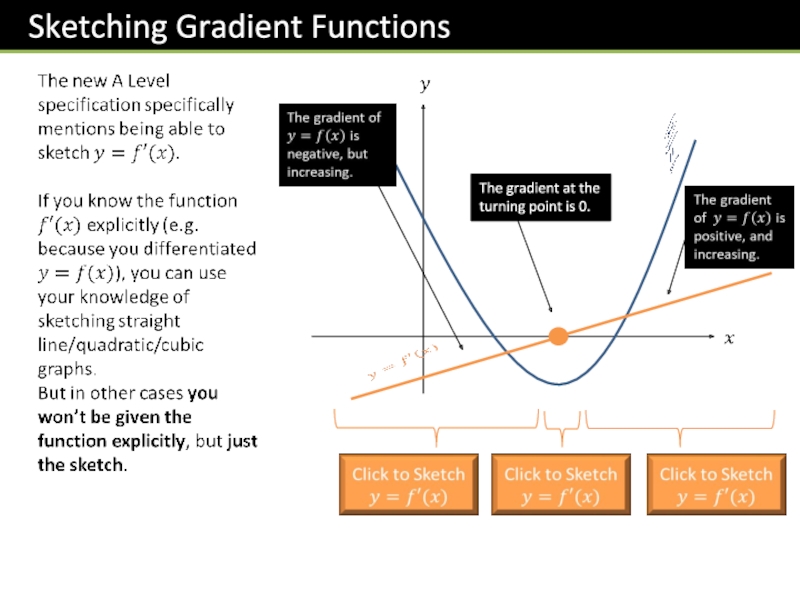
- 8. ?Helping Hand:“Row 4” of Pascal’s Triangle is:1 4 6 4 1You’re welcome.
- 9. ME-WOW!?
- 10. Examples:Power is 5, so multiply by 5 then reduce power by 5.????????
- 11. ???????12345
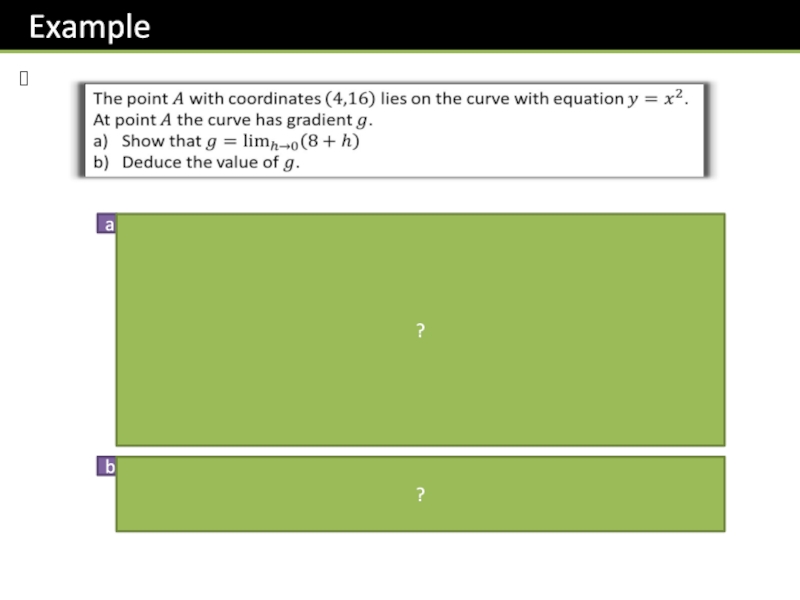
- 12. ???
- 13. 12345?????
- 14. abc???
- 15. abc???
- 16. 1. Turn roots into powers:2. Split up fractions.3. Expand out brackets.4. Beware of numbers in denominators!??????????
- 17. Differentiate the following.???
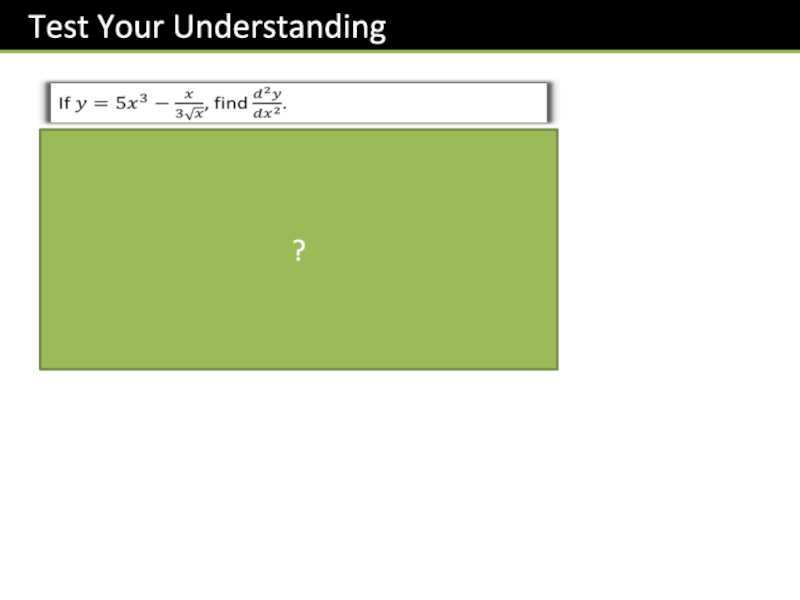
- 18. This just means “differentiate twice”. We’ll be looking at the ‘second derivative’ later in this chapter.?
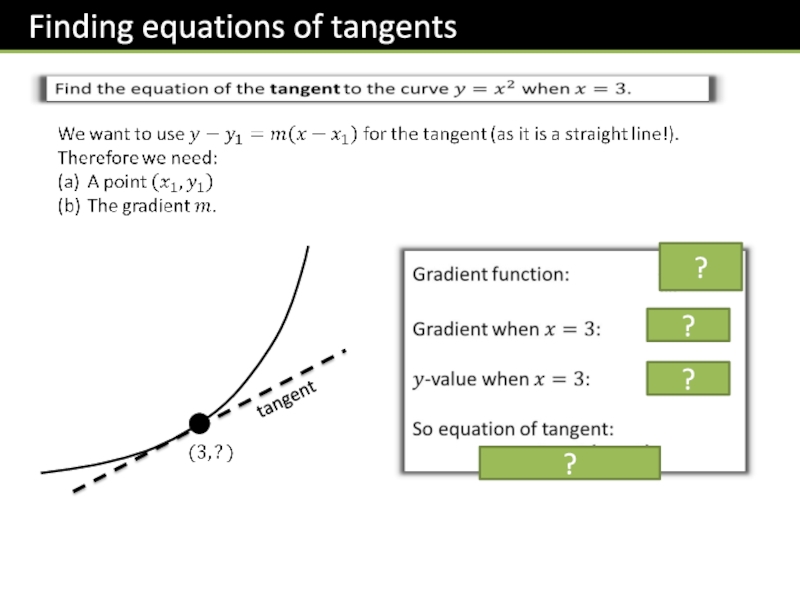
- 19. ????tangent
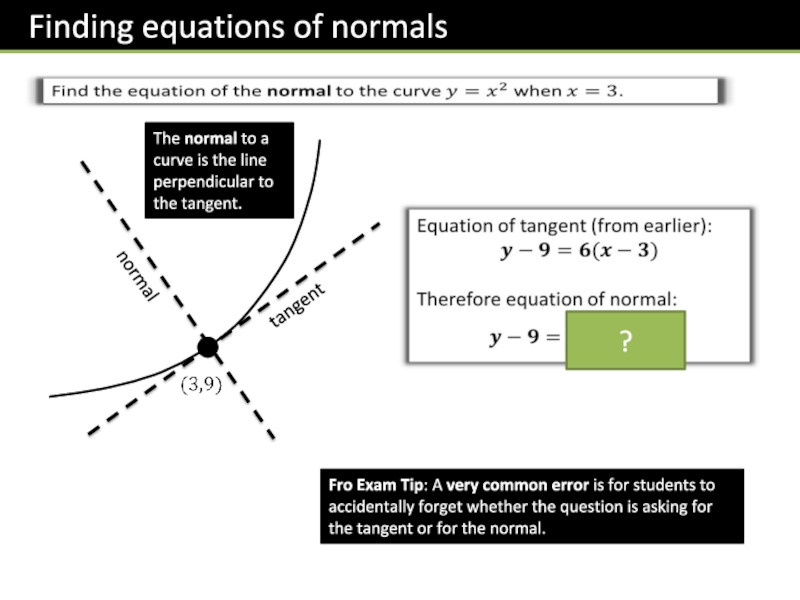
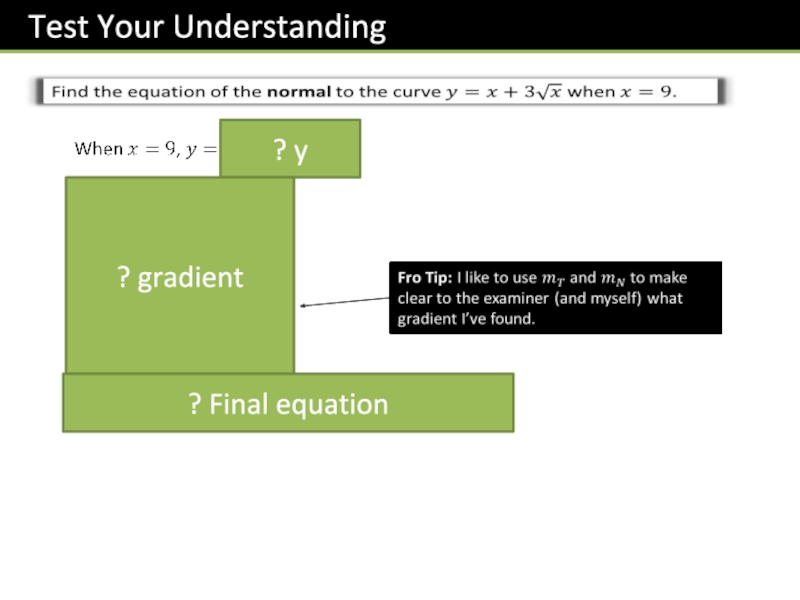
- 20. ?The normal to a curve is the
- 21. ? y? gradient? Final equation
- 22. Pearson Pure Mathematics Year 1/ASPages 269-270Extension12
- 23. Слайд 23
- 24. What do you think it means for
- 25. Fro Tip: To show a quadratic is
- 26. ??
- 27. When you differentiate once, the expression you
- 28. ME-WOW!
- 29. ??
- 30. ?
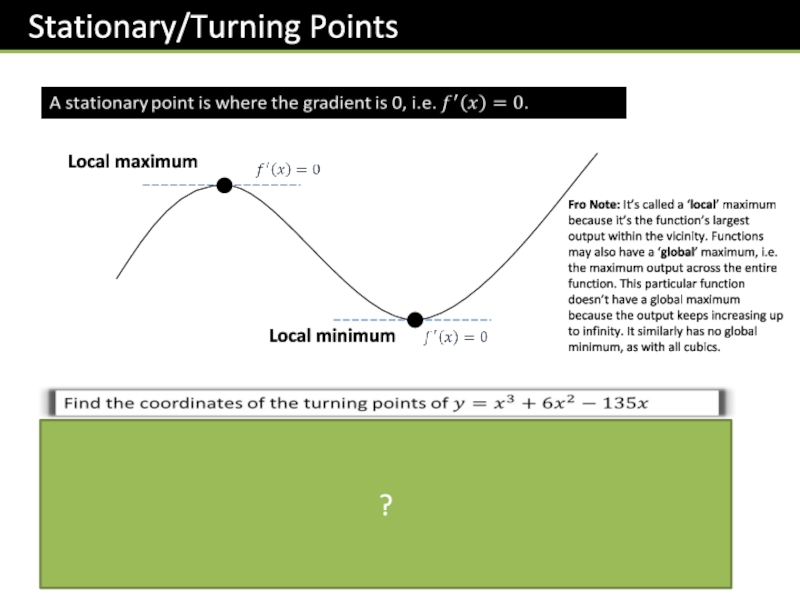
- 31. Local maximumLocal minimumFro Note: It’s called a
- 32. ? Method 1: Differentiation? Method 2:
- 33. There’s a third type of stationary point
- 34. ?????????Method 1: Look at gradient just before and just after point.
- 35. Method 1: Look at gradient just before and just after point.? Turning Point? Determine point type?
- 36. +vegradient0gradient-vegradient
- 37. ?
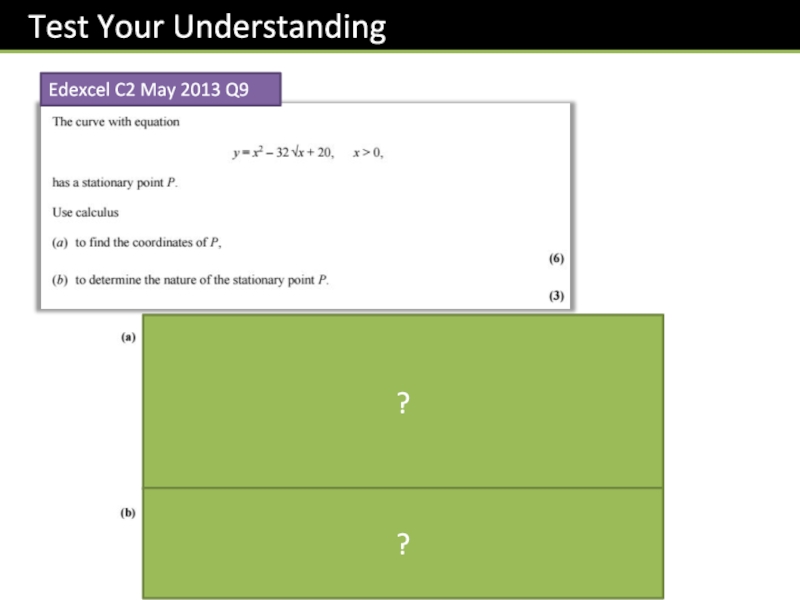
- 38. Edexcel C2 May 2013 Q9??
- 39. ? Vertical Asymptotes? Turning Points? Graph
- 40. Pearson Pure Mathematics Year 1/ASPage 276Extension1234
- 41. Therefore answer is 3.12
- 42. 3
- 43. 4
- 44. The gradient at the turning point is 0.
- 45. >>>>>>>Gradient is negative, but increasing.Fro Tip: Mentally
- 46. Solution >Gradient is negative, but increasing.Gradient is
- 47. Pearson Pure Mathematics Year 1/ASPage 278Extension1?
- 48. These are examples of optimisation problems: we’re
- 49. Real Life Maths!A sewage container fills at
- 50. Optimisation problems in an exam usually follow
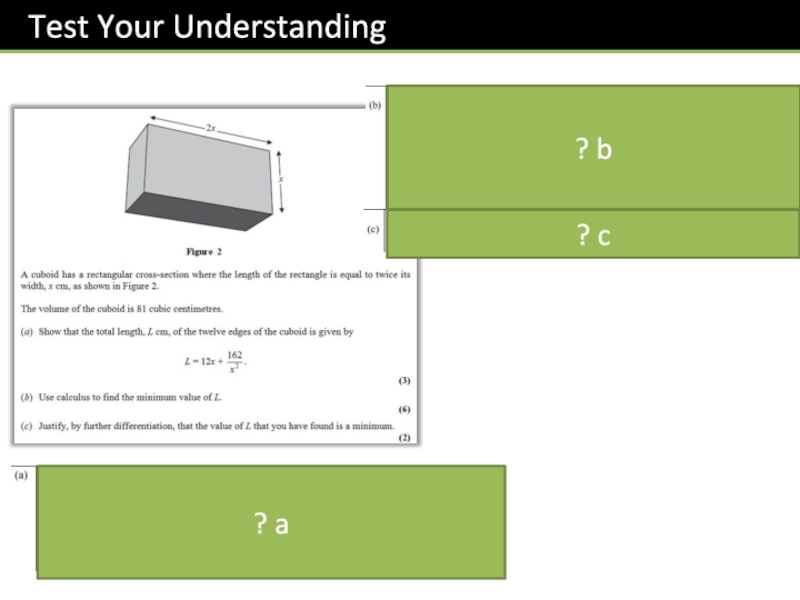
- 51. ? a? b? c
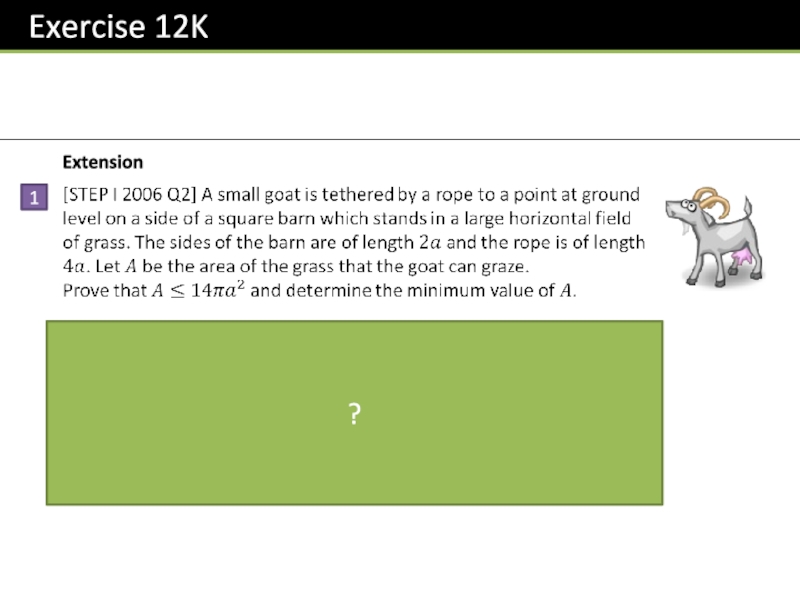
- 52. Extension1?
Слайд 21:: Find the derivative of polynomials.
2:: Find equations of tangents and
Those who have done either IGCSE Mathematics, IGCSE Further Mathematics or Additional Mathematics would have encountered this content. Otherwise it will be completely new!
3:: Identify increasing and decreasing functions.
5:: Find stationary points and determine their nature.
6:: Sketch a gradient function.
7:: Model real-life problems.
Слайд 3For a straight line, the gradient is constant:
At GCSE, you found
?
?
?
?
?
?
?
?
Слайд 4The question is then: Is there a method to work out
?
?
?
As the second point gets closer and closer, the gradient becomes a better approximation of the true gradient:
?
?
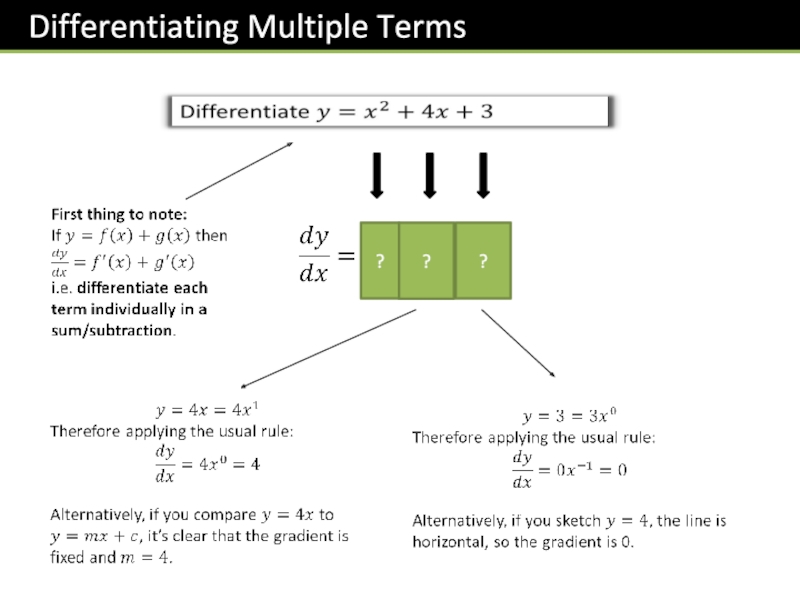
Слайд 161. Turn roots into powers:
2. Split up fractions.
3. Expand out brackets.
4.
?
?
?
?
?
?
?
?
?
?
Слайд 18This just means “differentiate twice”. We’ll be looking at the ‘second
?
Слайд 20?
The normal to a curve is the line perpendicular to the
tangent
normal
Fro Exam Tip: A very common error is for students to accidentally forget whether the question is asking for the tangent or for the normal.
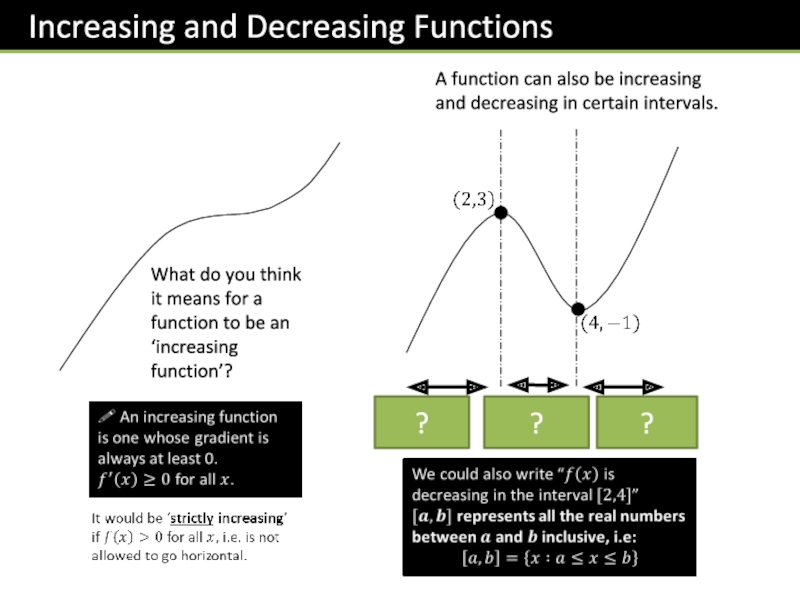
Слайд 24What do you think it means for a function to be
A function can also be increasing and decreasing in certain intervals.
?
?
?
Слайд 25Fro Tip: To show a quadratic is always positive, complete the
?
?
Слайд 27When you differentiate once, the expression you get is known as
Unsurprisingly, when we differentiate a second time, the resulting expression is known as the second derivative. And so on…
Leibniz’s
Newton’s
Lagrange’s
Original Function
First Derivative
Second Derivative
Слайд 31Local maximum
Local minimum
Fro Note: It’s called a ‘local’ maximum because it’s
?
Слайд 32?
Method 1: Differentiation
?
Method 2:
Completing the Square
Fro Note: Method 2 is
?
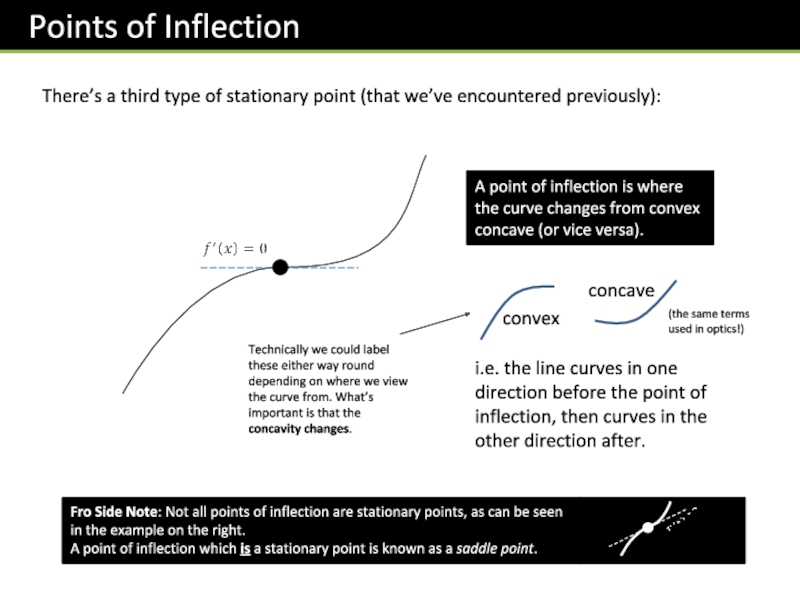
Слайд 33There’s a third type of stationary point (that we’ve encountered previously):
A
convex
concave
(the same terms used in optics!)
i.e. the line curves in one direction before the point of inflection, then curves in the other direction after.
Technically we could label these either way round depending on where we view the curve from. What’s important is that the concavity changes.
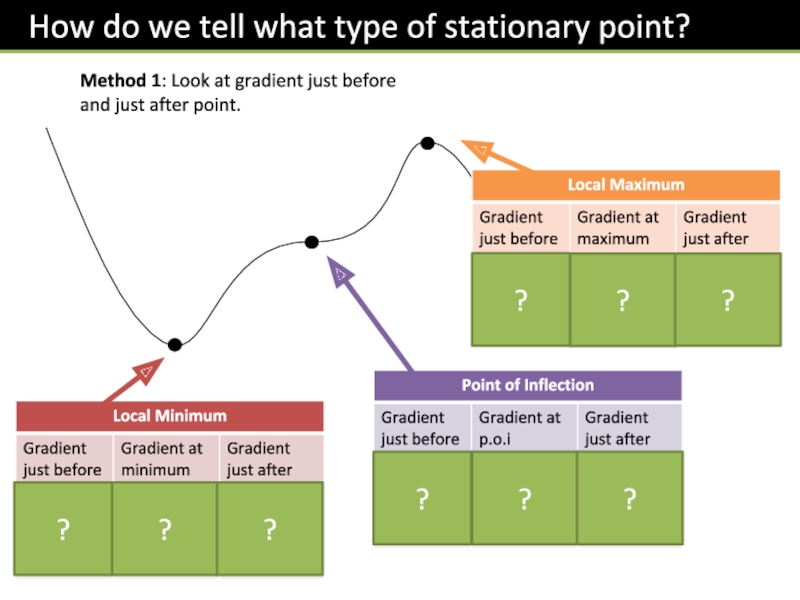
Слайд 35Method 1: Look at gradient just before and just after point.
?
? Determine point type
?
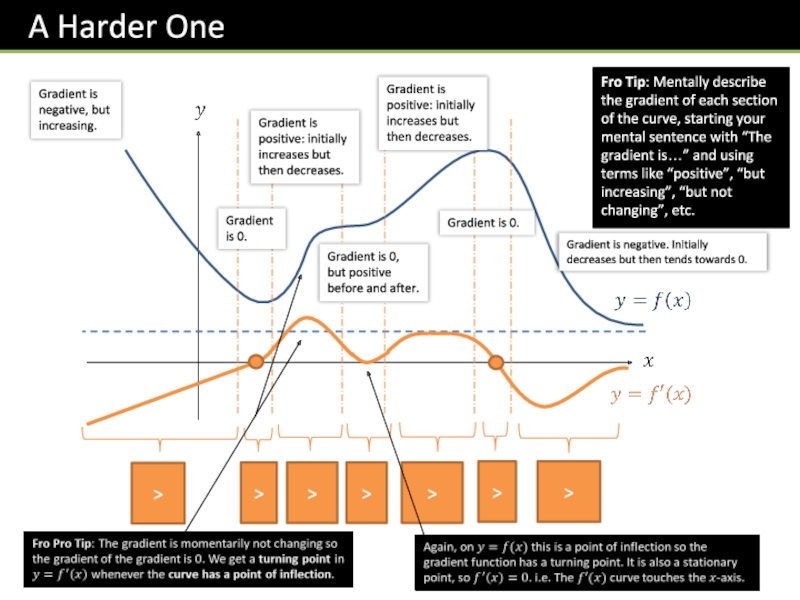
Слайд 45>
>
>
>
>
>
>
Gradient is negative, but increasing.
Fro Tip: Mentally describe the gradient of
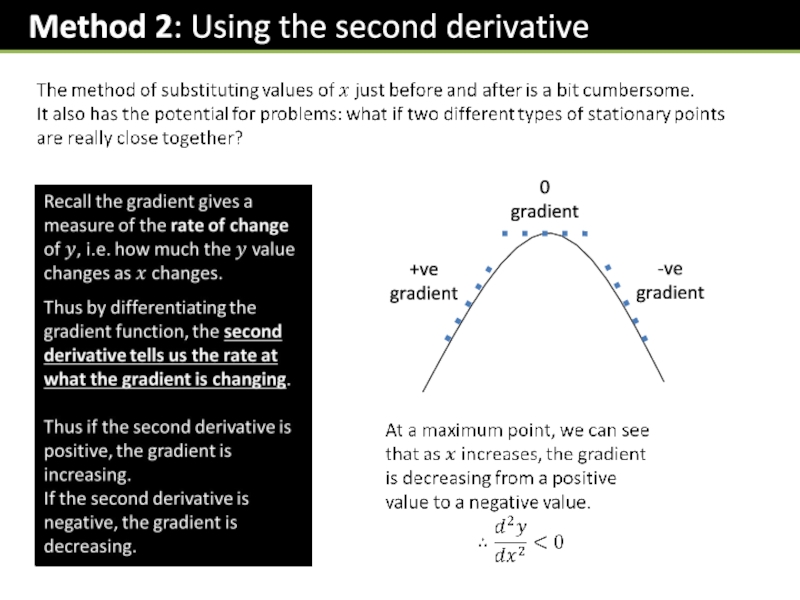
Gradient is 0.
Gradient is positive: initially increases but then decreases.
Gradient is 0, but positive before and after.
Gradient is positive: initially increases but then decreases.
Gradient is 0.
Gradient is negative. Initially decreases but then tends towards 0.
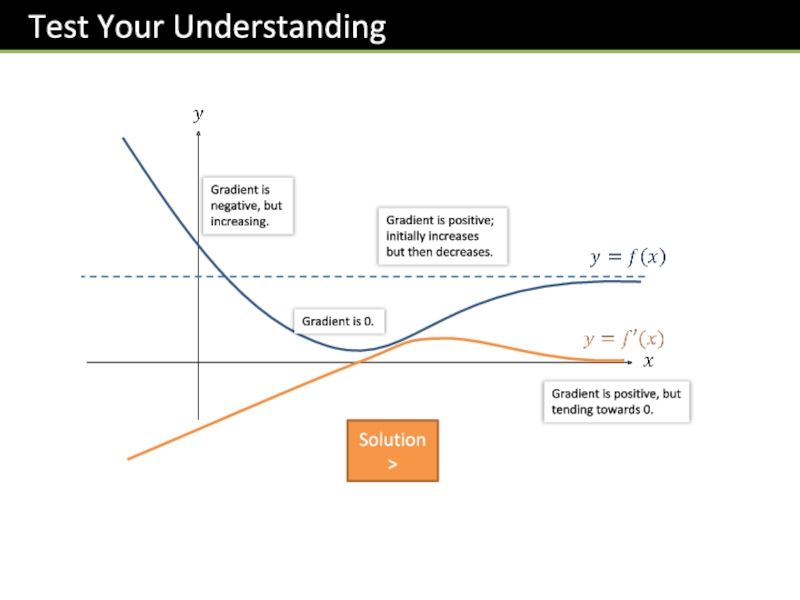
Слайд 46Solution >
Gradient is negative, but increasing.
Gradient is 0.
Gradient is positive; initially
Gradient is positive, but tending towards 0.
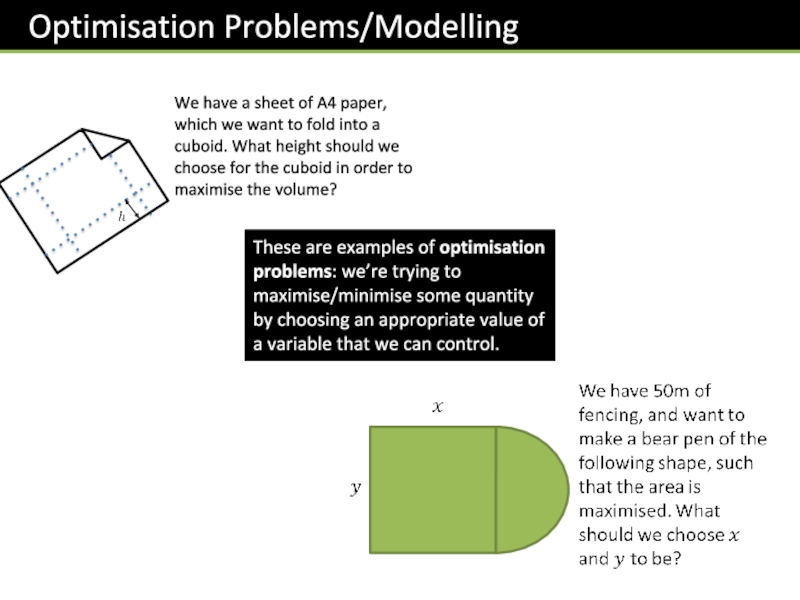
Слайд 48These are examples of optimisation problems: we’re trying to maximise/minimise some
We have a sheet of A4 paper, which we want to fold into a cuboid. What height should we choose for the cuboid in order to maximise the volume?
Слайд 49Real Life Maths!
A sewage container fills at a rate of 20
How could we use appropriate notation to represent this?
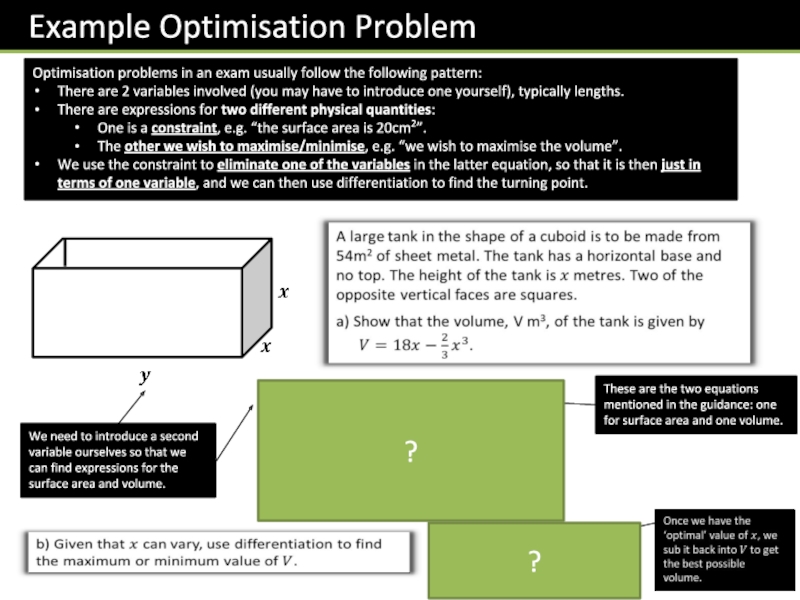
Слайд 50Optimisation problems in an exam usually follow the following pattern:
There are
There are expressions for two different physical quantities:
One is a constraint, e.g. “the surface area is 20cm2”.
The other we wish to maximise/minimise, e.g. “we wish to maximise the volume”.
We use the constraint to eliminate one of the variables in the latter equation, so that it is then just in terms of one variable, and we can then use differentiation to find the turning point.
We need to introduce a second variable ourselves so that we can find expressions for the surface area and volume.
These are the two equations mentioned in the guidance: one for surface area and one volume.
?
?