- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: Уравнения и неравенства, содержащие степень
Содержание
- 1. Презентация по математике на тему: Уравнения и неравенства, содержащие степень
- 2. «Кто смолоду делает и думает сам,
- 3. разминка
- 4. ОТВЕТИТЬ НА ВОПРОСЫ1.Что называется функцией?2.Что называется областью
- 5. Какая функция называется четной (нечетной)?
- 6. Если f(-х)=f(х) - четнаяЕсли f(-х)= -f(х)- нечетная
- 7. Как называют этот график ?
- 8. Найти область определения функции: 1) (- ∞; 1,5); 2 ) ( -∞; +∞);
- 9. ПОДЪЕМ К / II. этап «ПИКУ ЗНАНИЙ»
- 10. Решить уравнения:
- 11. Какие уравнения называются иррациональными? Что может появиться
- 12. Работа с учебникомРешить №198(1,2)
- 13. 1 группа
- 14. Кто определил класс уравнений любой степени, которые
- 15. Кто определил класс уравнений любой степени, которые разрешимы в радикалах?Кто ввел современное значение степени?
- 16. ПРИВАЛСчастливая случайность выпадает лишь на долю подготовленных
- 17. НЕМНОГО ИСТОРИИ
- 18. Нильс Хенрик Абель1802-1829АБЕЛЬ, НИЛЬС ХЕНРИК (Abel, Niels
- 19. АБЕЛЬ Нильс Хенрик (1802-1829), норвежский математик.
- 20. (1646 - 1716) Г.В. ЛЕЙБНИЦ– немецкий
- 21. III. ЭТАП КОНТРОЛЯ И САМОКОНТРОЛЯ
- 22. 1.ОБВАЛ
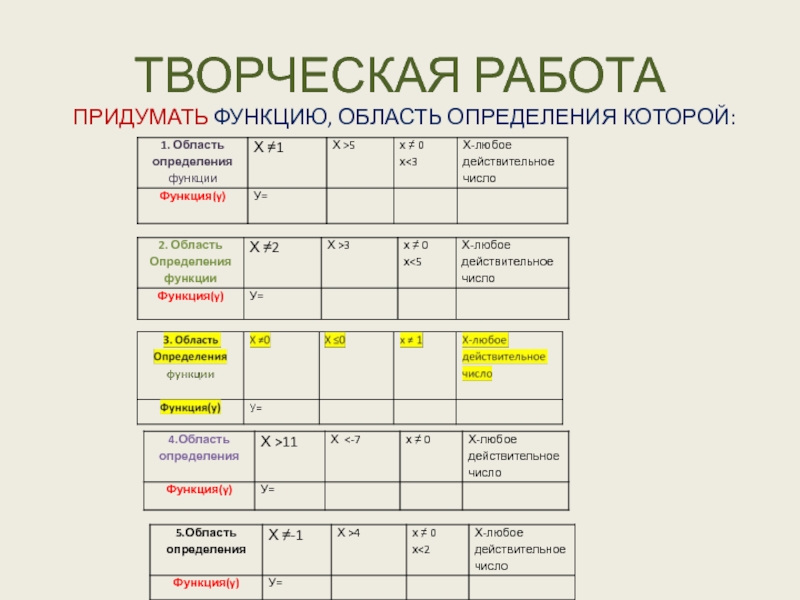
- 23. ТВОРЧЕСКАЯ РАБОТА ПРИДУМАТЬ ФУНКЦИЮ, ОБЛАСТЬ ОПРЕДЕЛЕНИЯ КОТОРОЙ:
- 24. ГИА
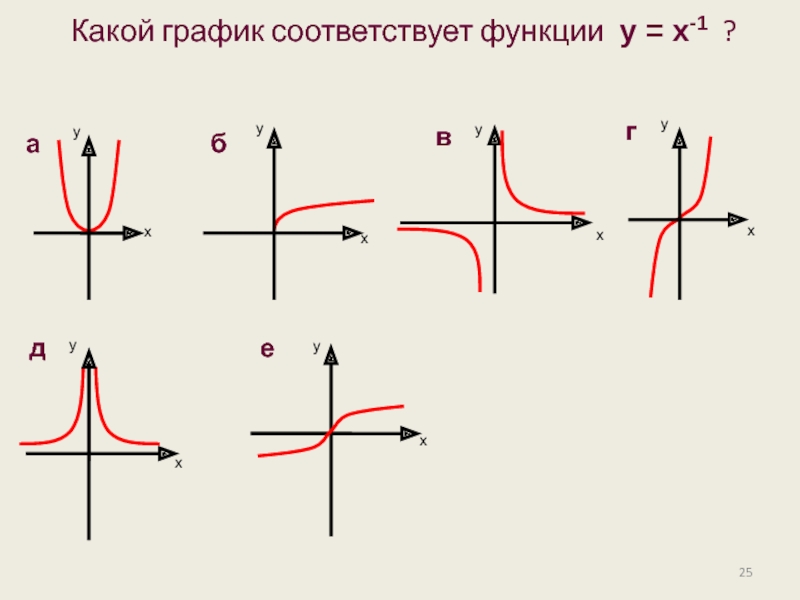
- 25. Какой график соответствует функции у = х-1 ?
- 26. ОТВЕТИТЬ НА ВОПРОСЫ «ДА» или «НЕТ»
- 27. ОТВЕТЫ1-ДА2-НЕТ3-НЕТ4-ДА5-ДА6- …
- 28. этап подведения итогов урокаI V.Оценочный лист
- 29. Решить№199(4), №200(2,4), №202(2,4)Домашнее заданиеэтапV.
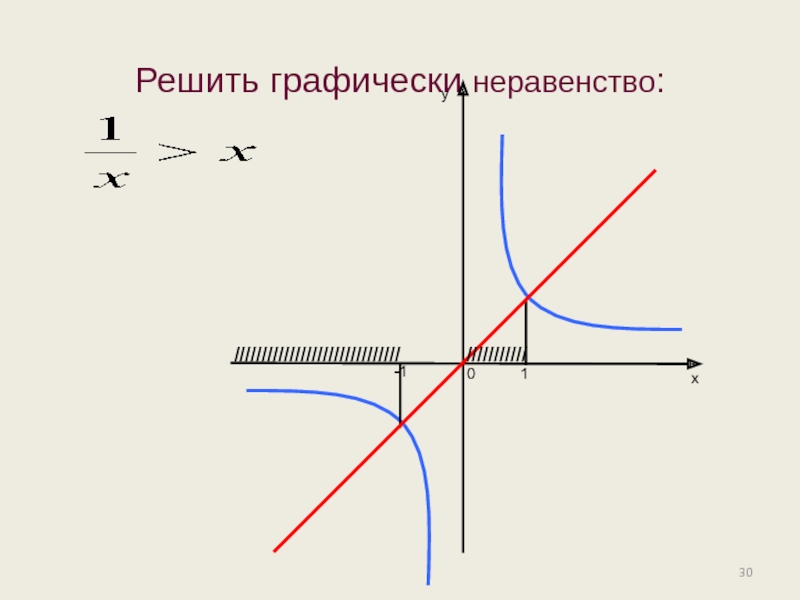
- 30. Решить графически неравенство: ух-11/////////////////////////////////////////0
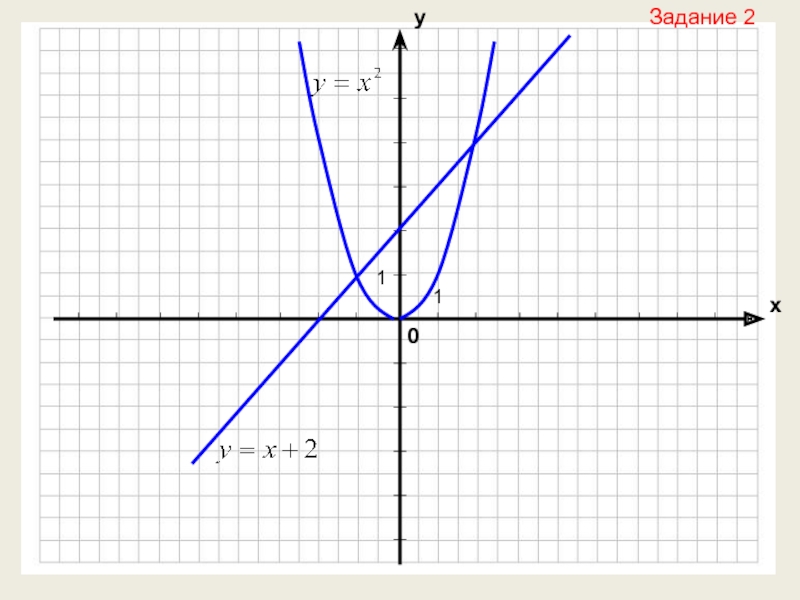
- 31. Задание 2
Слайд 4ОТВЕТИТЬ НА ВОПРОСЫ
1.Что называется функцией?
2.Что называется областью определения функции?
3. Что называется
4.Возрастание функции у= Хr на промежутке х больше или равно 0
5. Убывание функции у= Хr на промежутке х больше или равно 0
6.Какие уравнения называются иррациональными?
7.Что может появиться при возведении обеих частей уравнения в квадрат.
8.Что необходимо при этом сделать?
Слайд 7
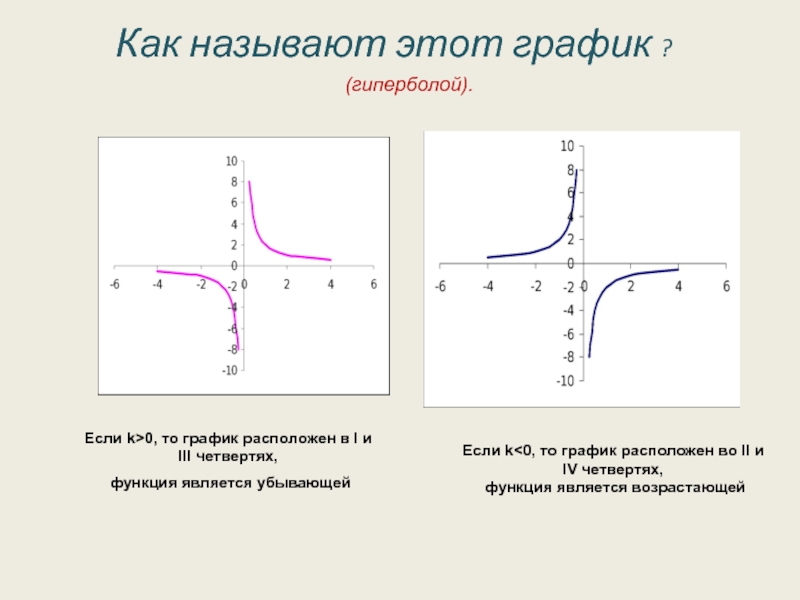
Как называют этот график ?
Если k>0, то график расположен в
функция является убывающей
Если k<0, то график расположен во II и IV четвертях,
функция является возрастающей
(гиперболой).
Слайд 11Какие уравнения называются иррациональными?
Что может появиться при возведении обеих частей
Что необходимо при этом сделать?
Слайд 131 группа
Кто определил класс уравнений любой степени,
которые разрешимы в радикалах?
Кто ввел современное значение степени?
РЕШИТЬ УРАВНЕНИЯ:
РЕШИТЬ УРАВНЕНИЯ:
Найти наибольшее целое
=
=
Слайд 14Кто определил класс уравнений
любой степени,
которые разрешимы в радикалах?
Кто ввел
РЕШИТЬ УРАВНЕНИЯ:
РЕШИТЬ УРАВНЕНИЯ:
9 - Е
25- А
2 - Ь
6 - Л
36 - Б
=
5 - Е
нет решений - А
16 – Т
18 - Д
3 – Р
10 - К
Слайд 15Кто определил класс уравнений
любой степени,
которые разрешимы в радикалах?
Кто ввел
Слайд 18Нильс Хенрик Абель
1802-1829
АБЕЛЬ, НИЛЬС ХЕНРИК (Abel, Niels Henrik) (1802–1829), норвежский математик
Слайд 19 АБЕЛЬ Нильс Хенрик (1802-1829), норвежский математик. Родился в семье пастора, учился
Первые исследования в основном относятся к алгебре. Автор трудов по теории чисел. На родине Абель не был признан при жизни,жил в нужде, умер от туберкулеза в 27 лет. В Королевском парке в г. Осло стоит скульптура сказочного юноши, попирающего двух поверженных чудовищ; по цоколю идет надпись
« Abel ».
Слайд 20 (1646 - 1716)
Г.В. ЛЕЙБНИЦ– немецкий математик, философ, историк, дипломат,