- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Угол между прямой и плоскостью(10 класс)
Содержание
- 1. Презентация по геометрии Угол между прямой и плоскостью(10 класс)
- 2. Методические рекомендации к урокуТема: Угол между прямой
- 3. αАВОСКДАНО: АВ = 6см,
- 4. Угол между прямой и плоскостью
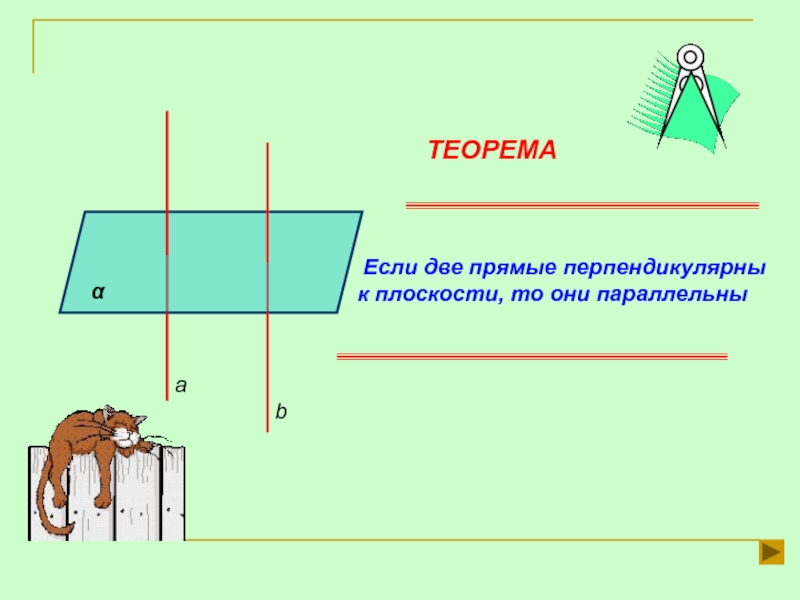
- 5. αаb ТЕОРЕМА Если две прямые перпендикулярны к плоскости, то они параллельны
- 6. FαмМ1 F1NПроекцией точки на плоскость называется основание
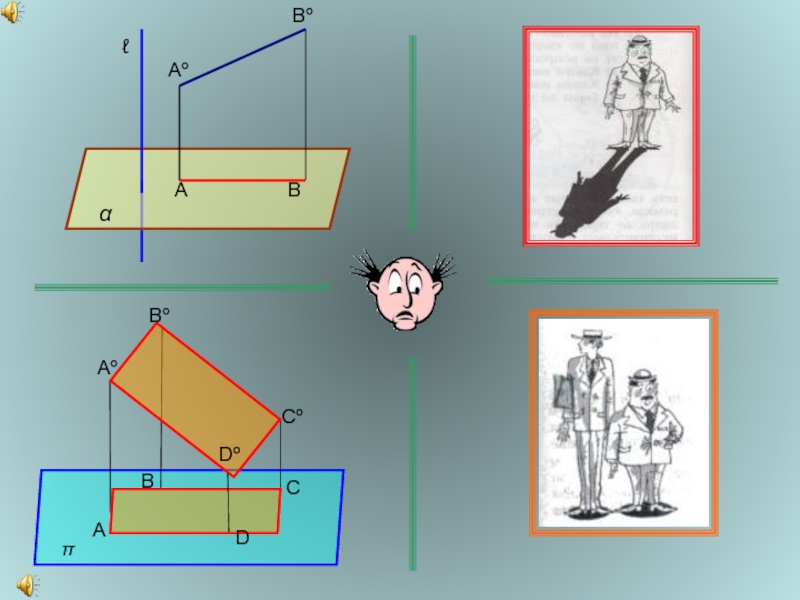
- 7. αℓАºВºАВAºBºCºDºABCDπ
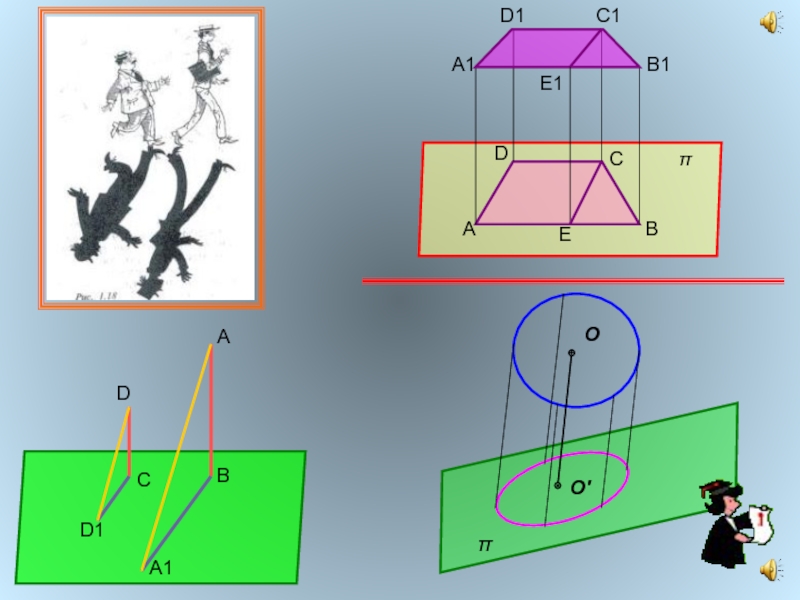
- 8. πА1B1E1AEBCDOO'πC1D1DD1CAA1B
- 9. ДОКАЗАТЬ: проекцией прямой а на плоскость α
- 10. αАМφφоОПРЕДЕЛЕНИЕ : Углом между прямой и плоскостью,
- 11. AB = d sin60°= d√3/2.ОТВЕТ: ВМ =
- 12. ТЕОРЕМА ФАЛЕСА Если на одной из двух
- 13. ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХНАКαqПрямая, проведенная в плоскости
- 14. № 150АКDСBДано: ABCD- прямоугольник, АК ⊥ АСВ
Слайд 2Методические рекомендации к уроку
Тема: Угол между прямой и плоскостью.
Цели урока.
Сформировать понятия
Формирование умений и навыков применения изученного материала к решению задач.
Развитие пространственного мышления.
Развитие геометрической культуры учащихся.
Этапы урока.
1. Актуализация знаний учащихся. Решение устных задач на готовых чертежах.(слайд 2). Задачи предлагаются по очереди. Управляющие кнопки позволяют напомнить утверждения, необходимые для решения задач.
2. Изучение нового.(слайды 5, 6, 7,8,9).
3. Закрепление изученного. (слайды 10, 13)
4. Подведение итогов.
5. Дом. задание.
Слайд 3
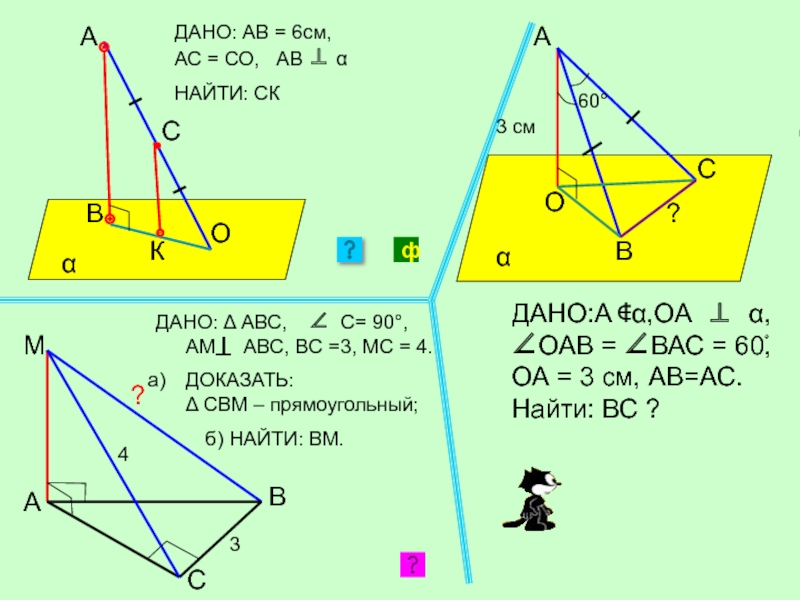
α
А
В
О
С
К
ДАНО: АВ = 6см,
НАЙТИ: СК
М
A
C
B
ДАНО: Δ АВС, ∠ С= 90°, AМ ABC, BC =3, МC = 4.
ДОКАЗАТЬ: Δ CBМ – прямоугольный;
б) НАЙТИ: BМ.
T
3
4
А
С
В
α
?
60°
3 см
ДАНО:А ∉α,ОА ⊥ α,
∠ОАВ = ∠ВАС = 60ْ,
ОА = 3 см, АВ=АС.
Найти: ВС ?
О
?
ф
Слайд 6
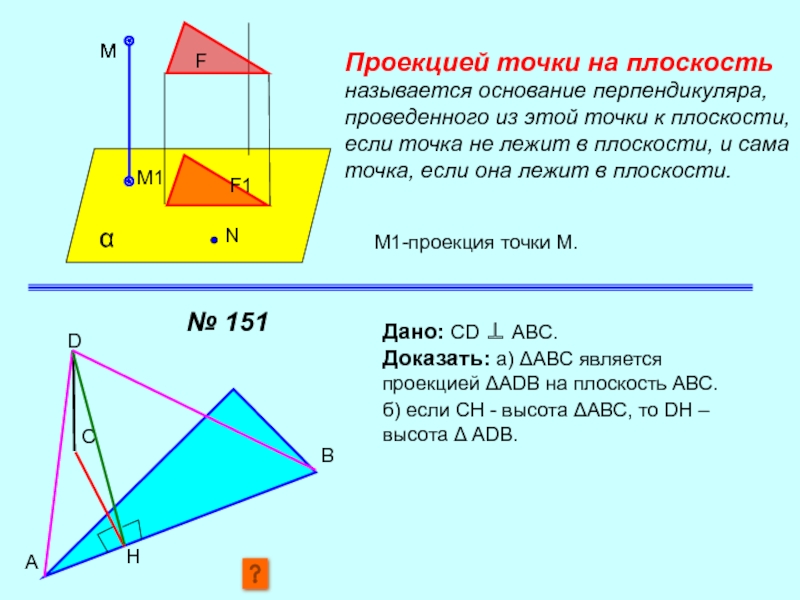
F
α
м
М1
F1
N
Проекцией точки на плоскость называется основание перпендикуляра, проведенного из этой
М1-проекция точки М.
A
C
B
H
D
Дано: CD ⊥ ABC.
Доказать: а) ΔАВС является проекцией ΔADB на плоскость АВС.
б) если СН - высота ΔАВС, то DH – высота Δ ADB.
№ 151
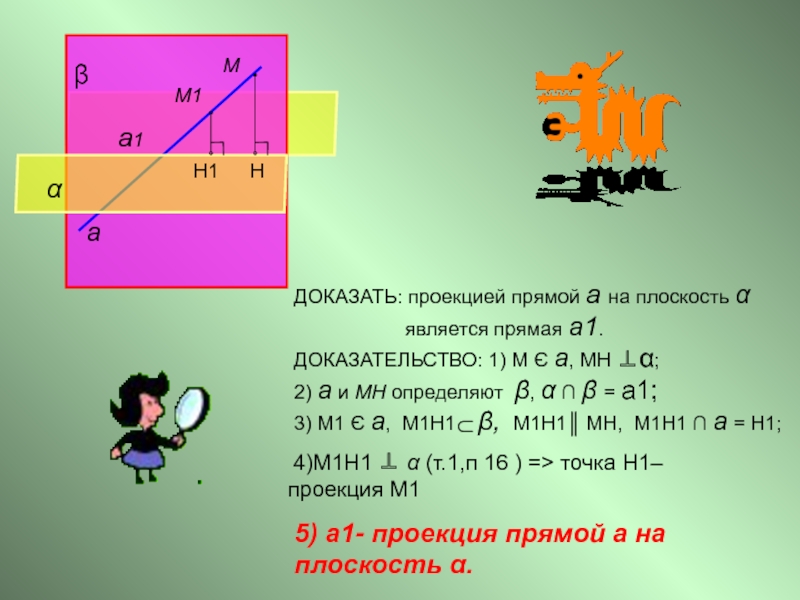
Слайд 9ДОКАЗАТЬ: проекцией прямой а на плоскость α
ДОКАЗАТЕЛЬСТВО: 1) М Є а, МН ⊥α;
2) а и МН определяют β, α ∩ β = а1;
3) М1 Є а, М1Н1 β, М1Н1║ МН, М1Н1 ∩ а = Н1;
5) а1- проекция прямой а на плоскость α.
4)М1Н1 ⊥ α (т.1,п 16 ) => точка Н1– проекция М1
β
а
а1
М
М1
∩
α
Н1
Н
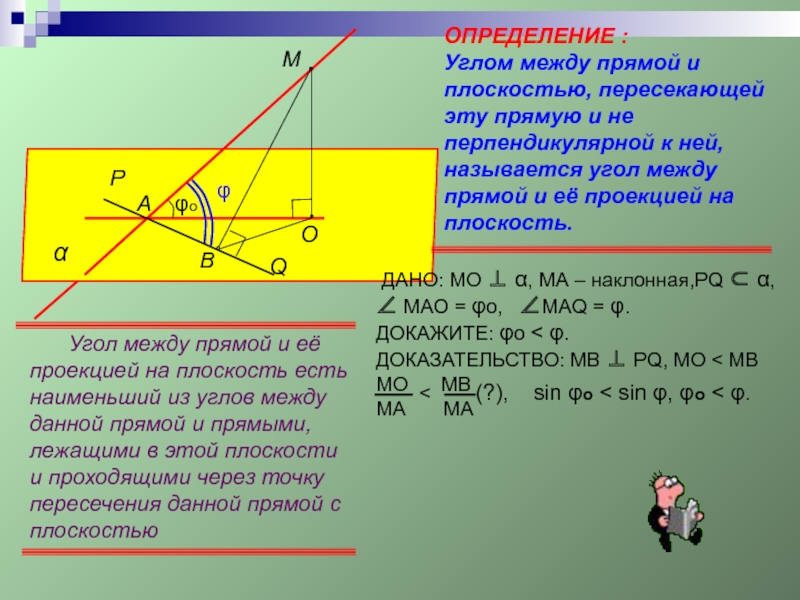
Слайд 10
α
А
М
φ
φо
ОПРЕДЕЛЕНИЕ :
Углом между прямой и плоскостью, пересекающей эту прямую и
B
O
Угол между прямой и её проекцией на плоскость есть наименьший из углов между данной прямой и прямыми, лежащими в этой плоскости и проходящими через точку пересечения данной прямой с плоскостью
ДАНО: МО ⊥ α, МА – наклонная,PQ ⊂ α,
∠ МАО = φо, ∠МАQ = φ.
ДОКАЖИТЕ: φо < φ.
ДОКАЗАТЕЛЬСТВО: MB ⊥ PQ, MO < MB
MO MB
MA MA
sin φo < sin φ, φo < φ.
P
Q
< (?),
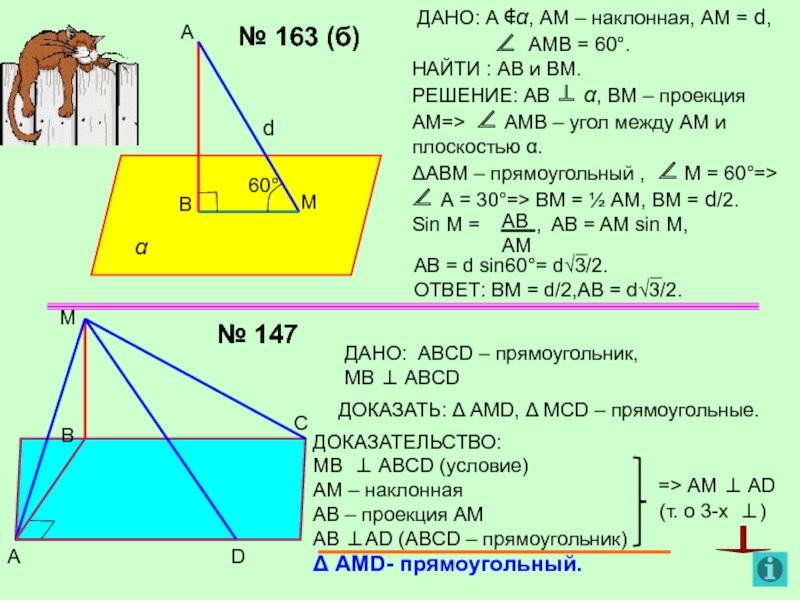
Слайд 11AB = d sin60°= d√3/2.
ОТВЕТ: ВМ = d/2,AB = d√3/2.
(т. о
=> АМ ⊥ AD
А
М
В
№ 163 (б)
ДАНО: А ∉α, АМ – наклонная, АМ = d,
∠ АМВ = 60°.
НАЙТИ : АВ и ВМ.
РЕШЕНИЕ: АВ ⊥ α, ВМ – проекция АМ=> ∠ АМВ – угол между АМ и плоскостью α.
ΔАВМ – прямоугольный , ∠ М = 60°=>
∠ А = 30°=> ВМ = ½ АМ, ВМ = d/2.
Sin M = , AB = AM sin M,
60°
α
d
А
В
М
С
D
ДАНО: ABCD – прямоугольник,
МВ ⊥ ABCD
ДОКАЗАТЬ: Δ AMD, Δ MCD – прямоугольные.
ДОКАЗАТЕЛЬСТВО:
MB ⊥ ABCD (условие)
AM – наклонная AB – проекция АМ
AB ⊥AD (ABCD – прямоугольник)
Δ AMD- прямоугольный.
№ 147
АВ
АМ
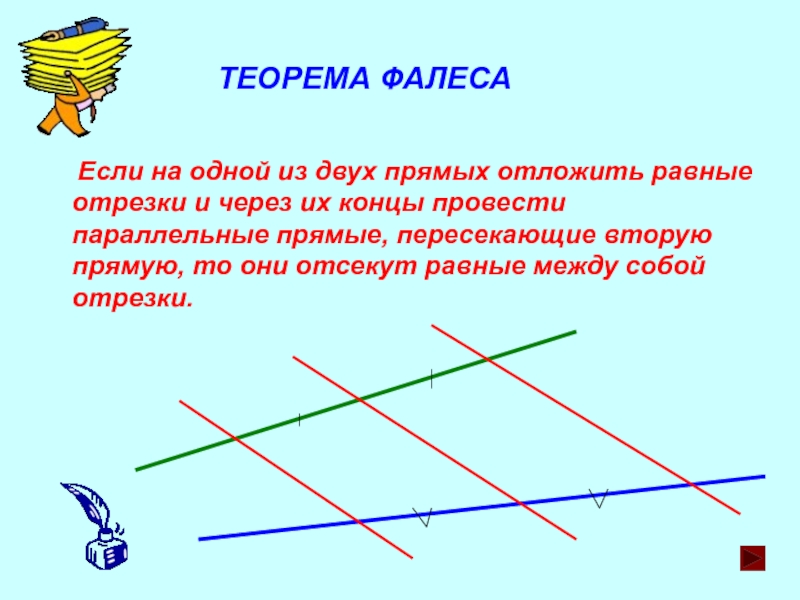
Слайд 12ТЕОРЕМА ФАЛЕСА
Если на одной из двух прямых отложить равные
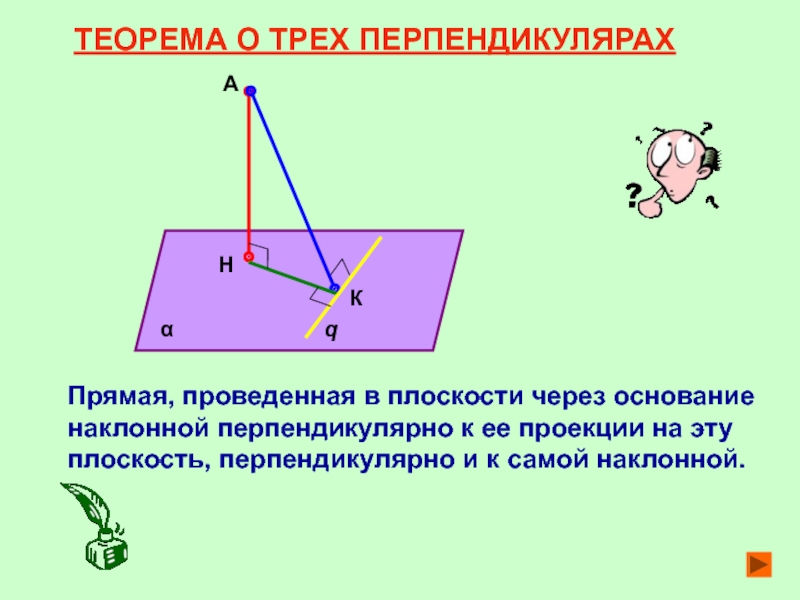
Слайд 13ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ
Н
А
К
α
q
Прямая, проведенная в плоскости через основание наклонной перпендикулярно
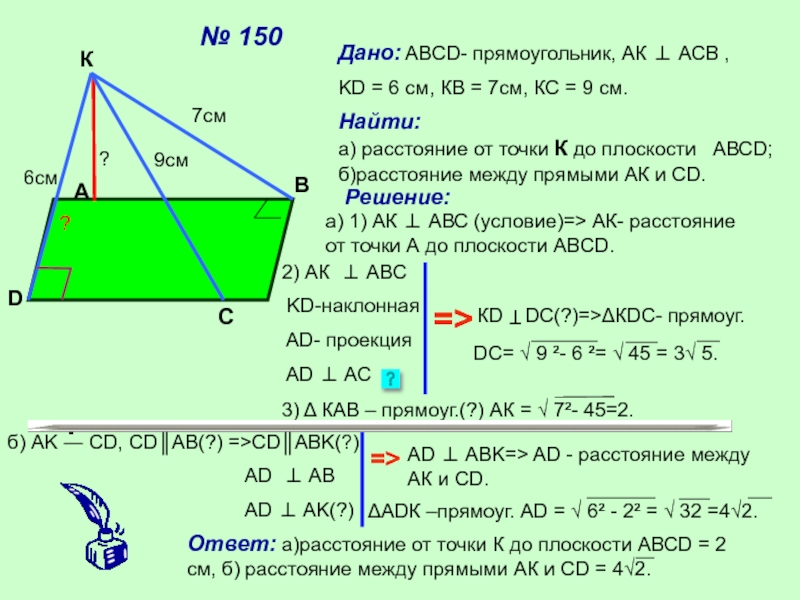
Слайд 14№ 150
А
К
D
С
B
Дано: ABCD- прямоугольник, АК ⊥ АСВ ,
KD = 6 см,
Найти: а) расстояние от точки К до плоскости АВСD; б)расстояние между прямыми АК и СD.
Решение:
7см
6см
9см
а) 1) АК ⊥ АВС (условие)=> АК- расстояние от точки А до плоскости ABCD.
?
2) АК ⊥ АВС
KD-наклонная
AD- проекция
AD ⊥ AC
=>
КD DC(?)=>ΔКDC- прямоуг.
T
DC= √ 9 ²- 6 ²= √ 45 = 3√ 5.
3) Δ КАВ – прямоуг.(?) АК = √ 7²- 45=2.
б) AK ― CD, CD║AB(?) =>CD║ABK(?)
AD ⊥ AB
AD ⊥ AK(?)
.
=>
AD ⊥ ABK=> AD - расстояние между АК и CD.
ΔADК –прямоуг. AD = √ 6² - 2² = √ 32 =4√2.
Ответ: а)расстояние от точки К до плоскости АВСD = 2 см, б) расстояние между прямыми АК и СD = 4√2.
?