- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Тригонометрические тождества
Содержание
- 1. Презентация по алгебре на тему Тригонометрические тождества
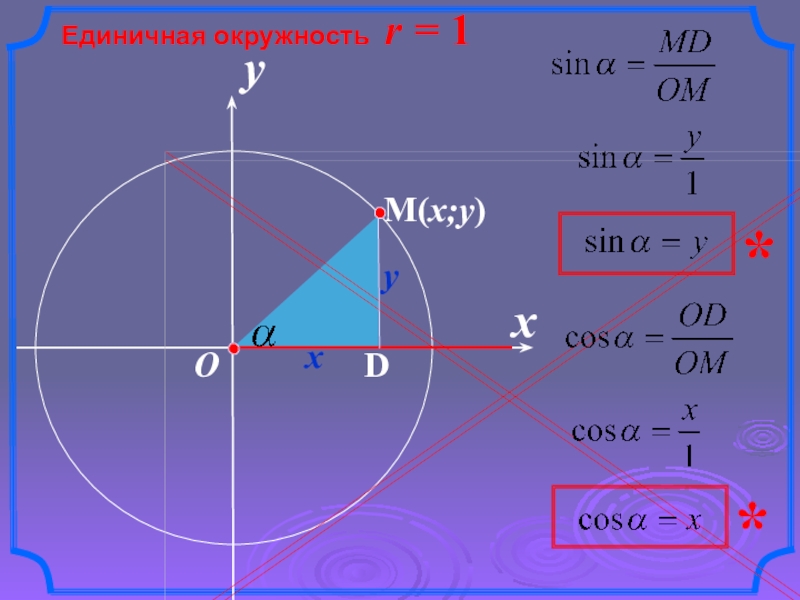
- 2. xЕдиничная окружность r = 1yOxy
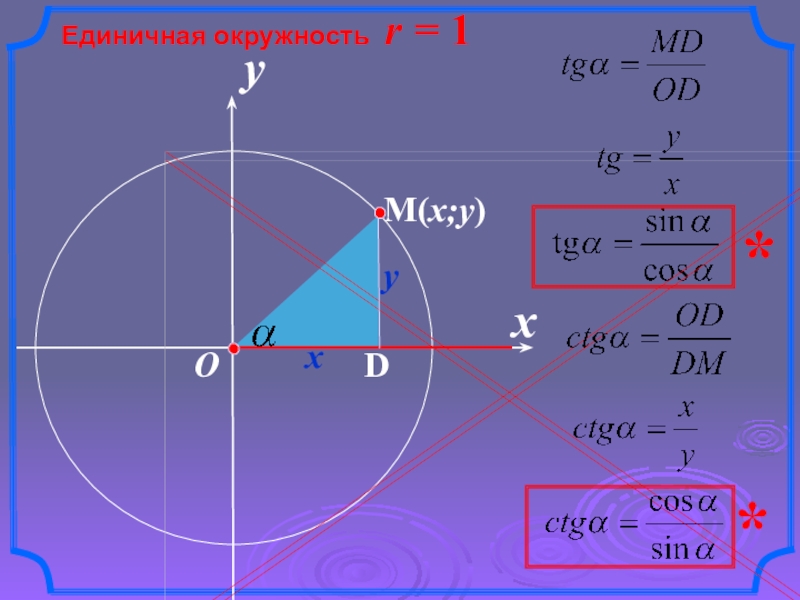
- 3. xЕдиничная окружность r = 1yOxy
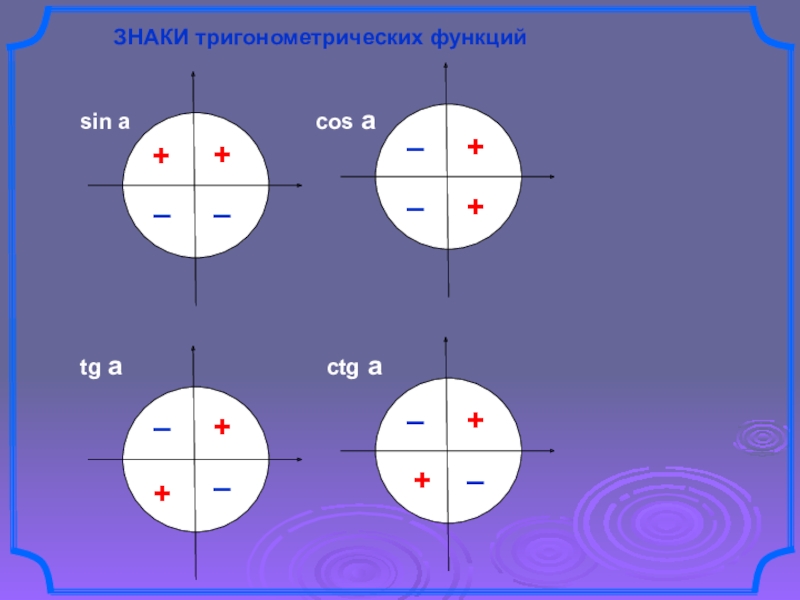
- 4. Слайд 4
- 5. Самостоятельная работаВариант №1Переведите данные числа из градусной
- 6. Почему знания тригонометрии необходимы для современного человека?
- 7. Тригонометрия (от греч. trigonon –
- 8. Основоположник аналитической теории тригонометрических функций.
- 9. Где применяется тригонометрияТригонометрические вычисления применяются практически во
- 10. Тригонометрия в физикеВ окружающем нас мире приходится
- 11. Слайд 11
- 12. Механические колебанияМеханическими колебаниями называют движения тел, повторяющиеся
- 13. Оптические иллюзииестественныесмешанныеискусственные
- 14. Теория радугиВпервые теория радуги была дана в
- 15. Связь движения рыб в воде с тригонометрическими
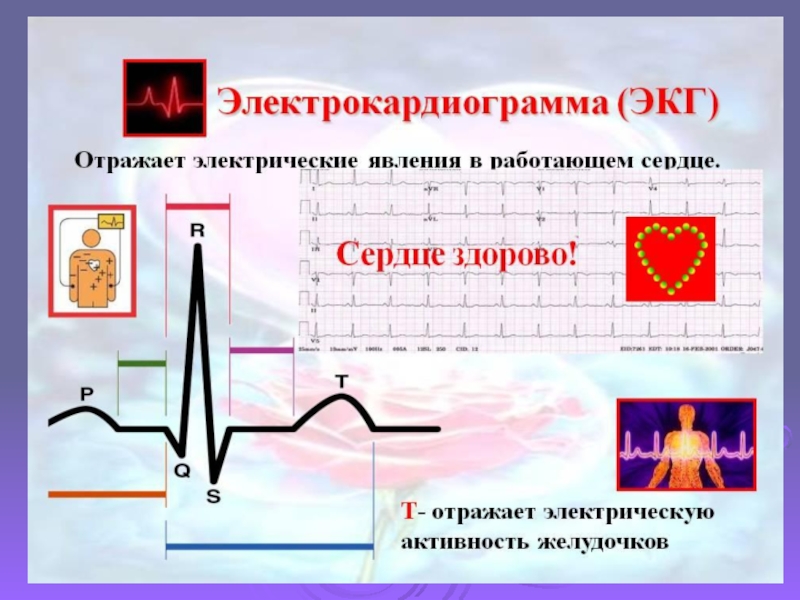
- 16. Тригонометрия играет важную роль в медицине. С
- 17. Связь биоритмов с тригонометриейМодель биоритмов можно построить
- 18. Тригонометрия прошла длинный путь развития. И теперь,
Слайд 5Самостоятельная работа
Вариант №1
Переведите данные числа из
градусной меры в радианную:
-45; 60.
2.
в градусную: П/3, П/9
Вариант №2
Переведите данные числа из
градусной меры в радианную:
390; - 1080.
2. Переведите из радианной меры
в градусную: П/10, П/4
Вариант №3
Переведите данные числа из
градусной меры в радианную:
40; 330.
2. Переведите из радианной меры
в градусную: П/5, П/20
Слайд 7 Тригонометрия (от греч. trigonon – треугольник, metro – метрия)
Что такое тригонометрия???
Слайд 9Где применяется тригонометрия
Тригонометрические вычисления применяются практически во всех сферах жизнедеятельности людей.
Слайд 10Тригонометрия в физике
В окружающем нас мире приходится сталкиваться с периодическими процессами,
Механические колебания
Гармонические колебания
Слайд 12Механические колебания
Механическими колебаниями называют движения тел, повторяющиеся точно через одинаковые промежутки
Примерами простых механических колебательных систем могут служить груз на пружине или математический маятник.
Слайд 14Теория радуги
Впервые теория радуги была дана в 1637 году Рене Декартом.
Радуга возникает из-за того, что солнечный свет испытывает преломление в капельках воды, взвешенных в воздухе по закону преломления:
sin α / sin β = n1 / n2
где n1=1, n2≈1,33 – соответственно показатели преломления воздуха и воды, α – угол падения, а β – угол преломления света.
Слайд 15Связь движения рыб в воде с тригонометрическими функциями
Движение рыб в воде
Слайд 16Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые
Биологические ритмы, биоритмы связаны с тригонометрией.
Тригонометрия в биологии
Какие биологические процессы связаны с тригонометрией?
Слайд 17Связь биоритмов с тригонометрией
Модель биоритмов можно построить с помощью графиков тригонометрических
Для этого необходимо ввести дату рождения человека ( день, месяц, год ) и длительность прогноза.