- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Свойства числовых неравенств
Содержание
- 1. Презентация по алгебре на тему Свойства числовых неравенств
- 2. Свойство 1. Если a>b и b>c, то a>c. Проверим на примере.Пусть a=6, b=0, c=−4, тогда, если 6>0 и 0>−4, то 6>−4.
- 3. Свойство 2. Если a>b, то a+c>b+c.Если к обеим частям
- 4. Свойство 3. Если a>b и k>0, то ak>bk.Если обе части неравенства умножить
- 5. Свойство 4. Если a>b и k
- 6. Слайд 6
- 7. Свойство 5 :Если a>b и c>d , то a+c>b+d .Неравенства одного смысла можно складывать.
- 8. Пример:1. известно, что 1,2 < x <
- 9. 2. Известно, что 1,2 < x <
- 10. Свойство 6 :Если a,b,c,d — положительные
- 11. 2. Известно, что 1,2
- 12. Свойство 7 :Если a и b — неотрицательные числа и a
- 13. Слайд 13
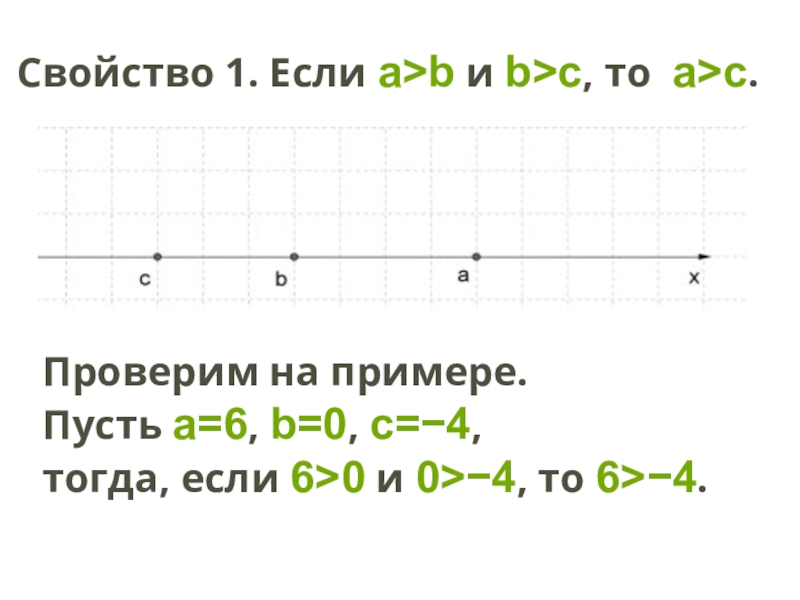
Слайд 2Свойство 1. Если a>b и b>c, то a>c.
Проверим на примере.
Пусть a=6, b=0, c=−4, тогда, если 6>0 и 0>−4, то 6>−4.
Слайд 3Свойство 2.
Если a>b, то a+c>b+c.
Если к обеим частям неравенства прибавить одно и
Пример: 18 > 5, 18+4 > 5+4
22 > 9
18 > 5, 18+ (-2) > 5+(-2)
16 > 3
Слайд 4Свойство 3. Если a>b и k>0, то ak>bk.
Если обе части неравенства умножить на одно и то
Пример:
известно, что 17,2 < x < 17,3. Найти 2x.
При умножении двойного неравенства на положительное число 2 получим неравенство того же смысла (т. е. знаки не изменятся).
17,2⋅2 < x⋅2 < 17,3⋅2;
34,4 < 2x < 34,6.
Слайд 5Свойство 4. Если a>b и k
изменится ( < на > , > на < ).
Пример:
известно, что 17,2
При умножении двойного неравенства на отрицательное число −2 получим неравенство противоположного смысла (т. е. знаки изменятся).
17,2⋅(−2) > x⋅(−2) > 17,3⋅(−2);
− 34,4 > −2x > −34,6;
− 34,6< −2x < − 34,4.
Слайд 8Пример:
1. известно, что 1,2 < x < 1,3 и 17
Найти x+y.
При сложении двойных неравенств одинакового смысла
получим неравенство того же смысла
(т. е. знаки не изменятся).
1,2 < x <1,3
17 < y < 18 ;
18,2 < x+y < 19,3.
Слайд 92. Известно, что 1,2 < x < 1,3 и 17< y
Найти x−y.
Умножив все части двойного неравенства
17 < y < 18 на (−1) и поменяв знаки неравенства, получим неравенство противоположного смысла.
17 < y < 18⋅(−1)
17⋅(−1) > y⋅(−1) > 18⋅(−1);
−17 > −y > −18;
−18 < −y < −17.
Сложим первое неравенство с полученным.
1,2 < x < 1,3
−18 < −y < −17
−16,8
Слайд 10 Свойство 6 :
Если a,b,c,d — положительные числа и
a>b ,
При умножении неравенств одного смысла, у которых левые и правые части — положительные числа, получается неравенство того же смысла.
Пример:
1. известно, что x<5 и y<11 .
Найти xy .
Перемножив неравенства, получим неравенство
того же смысла.
x < 5 и y < 11
x⋅y < 5⋅11;
х y < 55.
Слайд 112. Известно, что 1,2
(т. е. знаки не изменятся).
1,2 < x < 1,3 2 < y < 3×
1,2⋅2 < x⋅y < 1,3⋅3;
2,4 < xy < 3,9.