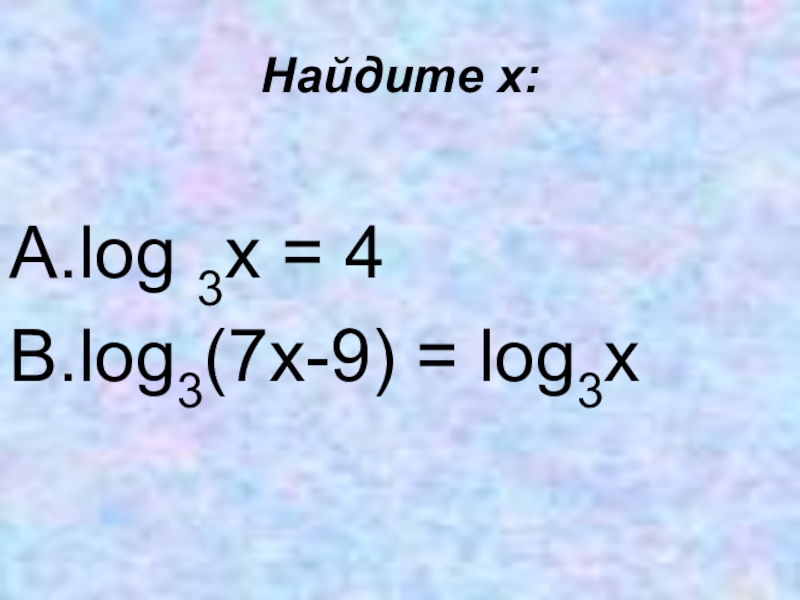- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Логарифмические уравнения(11 класс)
Содержание
- 1. Презентация по алгебре Логарифмические уравнения(11 класс)
- 2. Устная работа
- 3. Счет и вычисления – основа порядка в головеИоганн Генрих Песталоцци
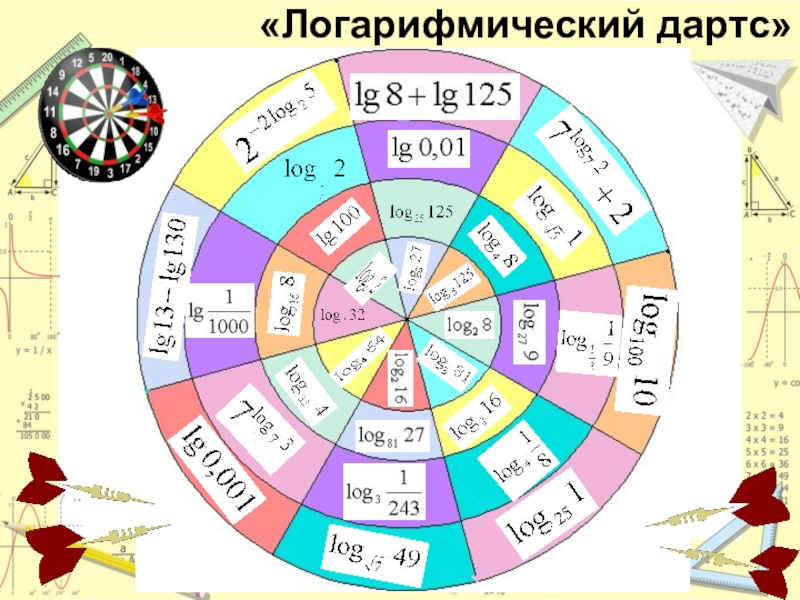
- 4. «Логарифмический дартс»
- 5. Найдите ошибки:log553 = 2log2162 = 83log24 = log2(4*3)3log23 = log227log327 = 4
- 6. Вычислите: log211 – log244 log1/64 + log1/69 2log525 +3log264
- 7. Найдите х: log 3x = 4 log3(7x-9) = log3x
- 8. ВзаимопроверкаРезультаты устной работы:«5» - 9-10 верных ответов«4»
- 9. Найдите х:log 3x = 4log3(7x-9) = log3x
- 10. Тема урока:ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ
- 11. Цели урока:Ввести определение логарифмического уравнения,Рассмотреть способы решения
- 12. Определение Уравнение, содержащее переменную под знаком
- 13. Определите уравнения являющиеся логарифмическими и не являющимися логарифмическими:
- 14. Являются логарифмическими Не являются логарифмическими
- 15. Методы решения логарифмических уравнений
- 16. Решение простейшего логарифмического уравнения
- 17. Методы решения логарифмических уравнений2. ПотенцированиемПод потенцированием понимается
- 18. Методы решения логарифмических уравненийПример 2Решите уравнение ЕслиПроверка:Потенцируя, получаем:
- 19. Методы решения логарифмических уравненийПример 2Решите уравнение ОДЗ:является корнем исходного уравнения.Потенцируя, получаем:
- 20. ЗАПОМНИ !Сладкая парочка!Два в одном!Два берега у
- 21. Методы решения логарифмических уравнений3. Применение свойств логарифмовПример 3Решите уравнение
- 22. Методы решения логарифмических уравнений4. Введения новой переменнойПример 4Решите уравнение ОДЗ: x>0 Переходя к переменной х, получим:
- 23. Методы решения логарифмических уравненийПо определению логарифма2. Потенцированием 3. Применение свойств логарифмов4. Введения новой переменной
- 24. Определи метод решения уравнений:По определениюПрименяя св-ва логарифмовПотенцированиемВведением
- 25. Орех познаний очень твердый,Но вы не смейте отступать.Его разгрызть поможет «Орбит»,А знания экзамен сдать.
- 26. Задания в группах№1 Найдите произведение корней уравнения
- 27. Алгоритм решения логарифмических уравненийВыписать условия, при которых
- 28. Проверочная работа!!!
- 29. Проверочная работаРешите логарифмические уравнения:1 вариант2 вариант
- 30. Предупредительный сигнал об окончании работы15Осталосьсекунд!
- 31. Конец работы!!!
- 32. Правильные ответы:Поменяйтесь бланками ответовКритерии выставления оценки:«5» -
- 33. Считай несчастным тот день или тот
- 34. Ну кто придумал эту математику !У меня
- 35. Домашнее заданиеП.39,№ 519(в,г),№ 520(в,г),№ 523 (б)№85 ,
- 36. Спасибо за работу
Устная работа
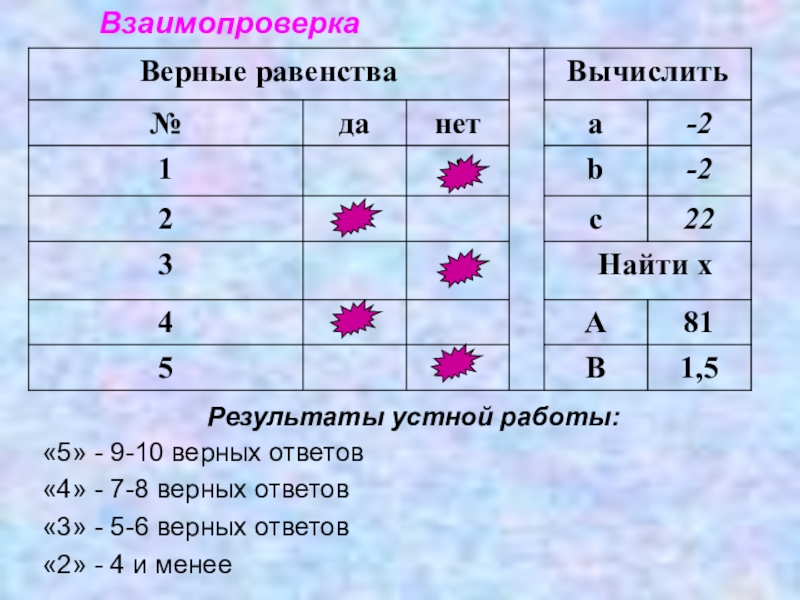
Слайд 8Взаимопроверка
Результаты устной работы:
«5» - 9-10 верных ответов
«4» - 7-8 верных ответов
«3»
- 5-6 верных ответов
«2» - 4 и менее
«2» - 4 и менее
Слайд 11Цели урока:
Ввести определение логарифмического уравнения,
Рассмотреть способы решения логарифмических уравнений,
Научиться решать логарифмические
уравнения,
Проверить первичные навыки решения логарифмических уравнений
Проверить первичные навыки решения логарифмических уравнений
Слайд 12 Определение
Уравнение, содержащее переменную под знаком логарифма или в основании
логарифма, называется логарифмическим
Например, или
Если в уравнении содержится переменная не под знаком логарифма, то оно не будет являться логарифмическим.
Например,
Например, или
Если в уравнении содержится переменная не под знаком логарифма, то оно не будет являться логарифмическим.
Например,
Слайд 16Решение простейшего логарифмического уравнения основано на применении определения логарифма и решении
равносильного уравнения
Методы решения логарифмических уравнений
1. По определению логарифма
Пример 1
Слайд 17Методы решения логарифмических уравнений
2. Потенцированием
Под потенцированием понимается переход от равенства, содержащего
логарифмы,
к равенству, не содержащему их:
Решив полученное равенство, следует сделать проверку корней,
т.к.применение формул потенцирования расширяет
область определения уравнения
Слайд 18Методы решения логарифмических уравнений
Пример 2
Решите уравнение
Если
Проверка:
Потенцируя, получаем:
Слайд 19Методы решения логарифмических уравнений
Пример 2
Решите уравнение
ОДЗ:
является корнем исходного уравнения.
Потенцируя, получаем:
Слайд 20
ЗАПОМНИ !
Сладкая парочка!
Два в одном!
Два берега у одной реки!
Два сапога –
пара!
Близки и неразлучны!
Нам не жить
друг без
друга!
Логарифм и ОДЗ
вместе
трудятся
везде!
ОН
- ЛОГАРИФМ!
ОНА
-
ОДЗ!
Слайд 21Методы решения логарифмических уравнений
3. Применение свойств логарифмов
Пример 3
Решите уравнение
Слайд 22Методы решения логарифмических уравнений
4. Введения новой переменной
Пример 4
Решите уравнение
ОДЗ: x>0
Переходя к переменной х, получим:
Слайд 23Методы решения логарифмических уравнений
По определению логарифма
2. Потенцированием
3. Применение свойств логарифмов
4.
Введения новой переменной
Слайд 24Определи метод решения уравнений:
По определению
Применяя
св-ва логарифмов
Потенцированием
Введением
новой переменной
Слайд 25Орех познаний очень твердый,
Но вы не смейте отступать.
Его разгрызть поможет «Орбит»,
А
знания экзамен сдать.
Слайд 26Задания в группах
№1 Найдите произведение корней уравнения
1) - 1,21
№2 Укажите
промежуток, которому принадлежит
корень уравнения
№3 Найдите сумму корней уравнения
1) 5
1) (- ∞;-2]
2) - 0,9
3) 0,81
4) 1,21
3) [1;2]
2) [-2;1]
4) [2;+∞)
2) 25,2
3) -25,2
4) - 5
Слайд 27Алгоритм решения логарифмических уравнений
Выписать условия, при которых логарифмическое уравнение определено
Выбрать метод
решения
Решить уравнение
Для найденных корней проверить выполнение условий пункта 1
При записи ответа исключить посторонние корни
Решить уравнение
Для найденных корней проверить выполнение условий пункта 1
При записи ответа исключить посторонние корни
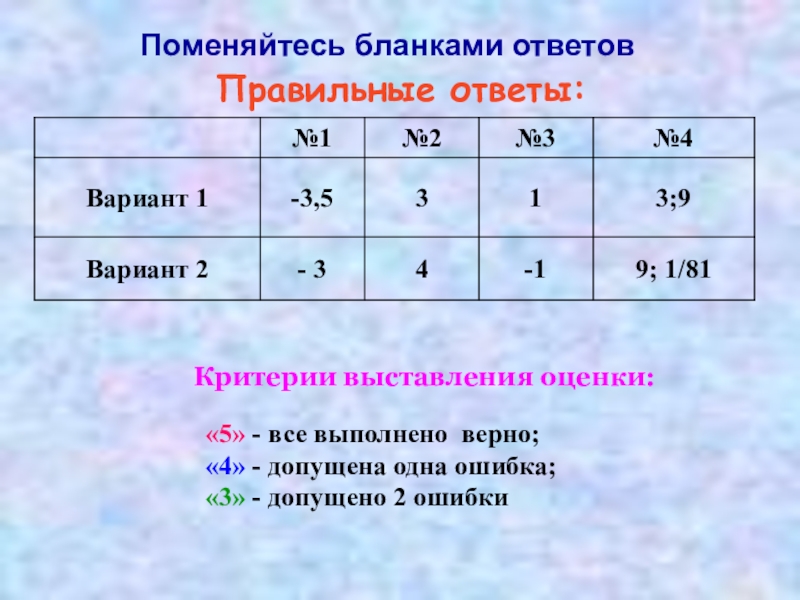
Слайд 32Правильные ответы:
Поменяйтесь бланками ответов
Критерии выставления оценки:
«5» - все выполнено верно;
«4» -
допущена одна ошибка;
«3» - допущено 2 ошибки
«3» - допущено 2 ошибки
Слайд 33Считай несчастным тот день или
тот час, в который ты
не
усвоил ничего нового, ничего не прибавил к своему образованию.
Ян Амос Коменский
Оцените свои знания и умения на уроке.
Слайд 34Ну кто придумал эту математику !
У меня всё получилось!!!
Надо решить ещё
пару примеров.
Все понятно , легко,
нет вопросов
Возникали трудности , есть вопросы
Трудно, много вопросов
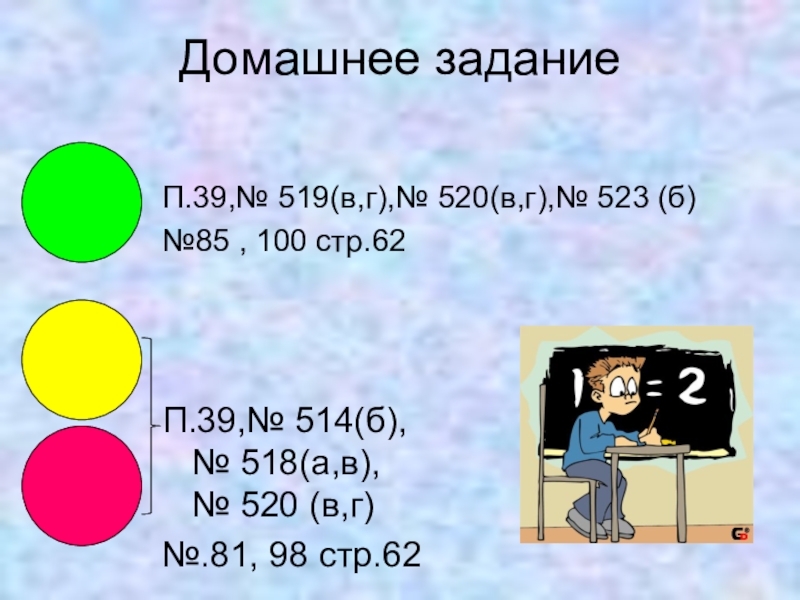
Слайд 35Домашнее задание
П.39,№ 519(в,г),№ 520(в,г),№ 523 (б)
№85 , 100 стр.62
П.39,№ 514(б),
№ 518(а,в),
№
520 (в,г)
№.81, 98 стр.62
№.81, 98 стр.62
