- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад открытого урока по математике в 8 классе Графики квадратичной функции
Содержание
- 1. Презентация открытого урока по математике в 8 классе Графики квадратичной функции
- 2. Графики функцийу=ах2+n и у=а(х-m)2Тема урока: Всякое учение
- 3. Цели урока:1. Обучающая: изучить правила построения графиков
- 4. Оборудование: В классе: доска, мел; компьютер (проектор.У
- 5. Устный опрос Сформулировать определение квадратичной функции;Что является
- 6. Задание 1 Задание 2ЗАДАНИЕ 3
- 7. Практическое выполнение задания в тетрадиВ одной системе
- 8. Задание 1Построить в одной системе координат графики функции y=x2 , y=x2-5 и y=x2+5
- 9. Задание 2Построить в одной системе координат графики функций у=2х2, у=2(х-5)2, у=2(х+4)2
- 10. Задание 3Построить в одной системе координат графики
- 11. Проверь себяЗадание 1 Задание 2Задание 3
- 12. Вывод: График функции у=ах2 +n является параболой,
- 13. Вывод :График функции у=а(х-m)2 является
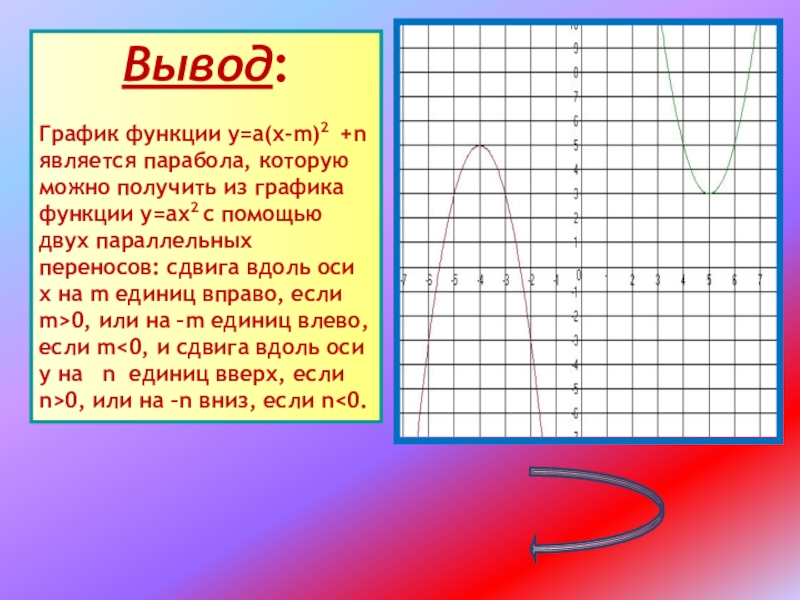
- 14. Вывод: График функции у=а(х-m)2 +n является парабола,
- 15. Самостоятельная работа.Построить графики функций: а) y=-2(x+3)²+1
- 16. Проверь себя.
- 17. Подведение итогов урока:1. Сформулируйте правило: как построить
- 18. Правильные ответы:График функции у=а(х-m)²+n можно получить из
- 19. Домашнее задание
Графики функцийу=ах2+n и у=а(х-m)2Тема урока: Всякое учение и всякое обучение основано на некотором уже ранее имеющемся знании Аристотель
Слайд 1Алгебра 8 класс
(А.Г.Мордкович)
Филиал МБОУ Аркинской СОШ
с. Лубошево
Учитель математики
Куракина Т.И.
Слайд 2Графики функций
у=ах2+n и у=а(х-m)2
Тема урока:
Всякое учение и всякое обучение основано
на некотором уже ранее имеющемся знании
Аристотель
Аристотель
Слайд 3Цели урока:
1. Обучающая: изучить правила построения графиков функций y=ax²+n,
y=a(x-m)²,
у=а(х-m)² +n, если известен график функции y=ax².
2. Развивающая: развивать навыки построения графиков функций y=ax²+n,
y=a(x-m)², у=а(х-m)² +n, путём параллельного переноса вдоль оси ОУ, оси 0Х.
3. Воспитательная: воспитание аккуратности при выполнении чертежей.
2. Развивающая: развивать навыки построения графиков функций y=ax²+n,
y=a(x-m)², у=а(х-m)² +n, путём параллельного переноса вдоль оси ОУ, оси 0Х.
3. Воспитательная: воспитание аккуратности при выполнении чертежей.
Слайд 4Оборудование:
В классе: доска, мел; компьютер (проектор.
У учеников: цветные карандаши, линейки,
ручки, рабочие тетради и тетради – конспекты.
План урока.
1. Оргмомент–2мин.
2. Проверка домашнего задания–5мин.
3. Устный опрос – 7 мин.
4. Практическая часть–20мин.
5. Самостоятельная работа – 8 мин
6. Подведение итогов урока.
Домашнее задание – 3 мин.
План урока.
1. Оргмомент–2мин.
2. Проверка домашнего задания–5мин.
3. Устный опрос – 7 мин.
4. Практическая часть–20мин.
5. Самостоятельная работа – 8 мин
6. Подведение итогов урока.
Домашнее задание – 3 мин.
Слайд 5Устный опрос
Сформулировать определение квадратичной функции;
Что является графиком квадратичной функции?
Сформулировать свойства
квадратичной функции у=ах2 при а>0, a<0.
Как из графика функции у=ах2 можно получить график функции у=ах2 + n; график функции у=а(х-m)2
Как из графика функции у=ах2 можно получить график функции у=ах2 + n; график функции у=а(х-m)2
Слайд 7Практическое выполнение задания в тетради
В одной системе координат построить графики функций
в тетрадях:
А)у = 1/2 x2; y = 1/2x2 +4; y =1/2x2 -3;
Б)у=-1/3х2 , y = -1/3(x-2)2 , y = -1/3(x+3)2 ,
А)у = 1/2 x2; y = 1/2x2 +4; y =1/2x2 -3;
Б)у=-1/3х2 , y = -1/3(x-2)2 , y = -1/3(x+3)2 ,
Слайд 10Задание 3
Построить в одной системе координат графики функций у=2х2 ,у= 2(х-5)2+3,
у=-2(х+4)2-5
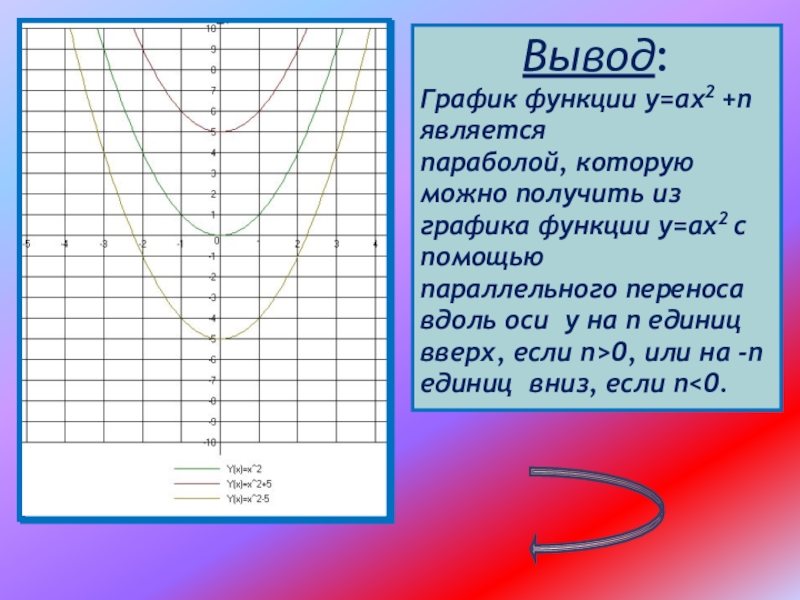
Слайд 12Вывод:
График функции у=ах2 +n является
параболой, которую можно получить из
графика функции у=ах2 с помощью
параллельного переноса вдоль оси у на n единиц вверх, если n>0, или на -n единиц вниз, если n<0.
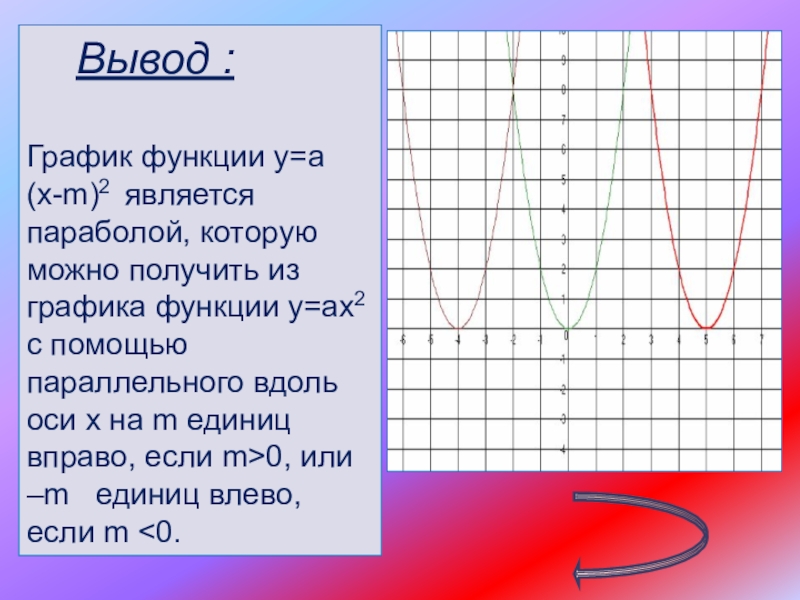
Слайд 13 Вывод :
График функции у=а(х-m)2 является параболой, которую можно получить
из графика функции у=ах2 с помощью параллельного вдоль оси х на m единиц вправо, если m>0, или –m единиц влево, если m <0.
Слайд 14Вывод:
График функции у=а(х-m)2 +n является парабола, которую можно получить из
графика функции у=ах2 с помощью двух параллельных переносов: сдвига вдоль оси х на m единиц вправо, если m>0, или на –m единиц влево, если m<0, и сдвига вдоль оси у на n единиц вверх, если n>0, или на –n вниз, если n<0.
Слайд 15Самостоятельная работа.
Построить графики функций:
а) y=-2(x+3)²+1
b) y=0,5(x-2)²-2
c) y= -(x+4)²-0,5
c) y= -(x+4)²-0,5
Слайд 17Подведение итогов урока:
1. Сформулируйте правило:
как построить график функции
у=а(х-m)²
+n, если известен график функции у=ах² ?
2. Что из сегодняшнего урока запомнить на будущее?
2. Что из сегодняшнего урока запомнить на будущее?
Слайд 18Правильные ответы:
График функции у=а(х-m)²+n можно получить из графика функции у=ах²
с помощью двух параллельных переносов: сдвига вдоль оси х на m единиц вправо, если m>0, или на –m единиц влево, если m<0, и сдвига вдоль оси у на n единиц вверх, если n>0, или на –n вниз, если n<0.
Правила построения графиков функций с помощью одного или двух параллельных переносов относительно осей координат.
Правила построения графиков функций с помощью одного или двух параллельных переносов относительно осей координат.