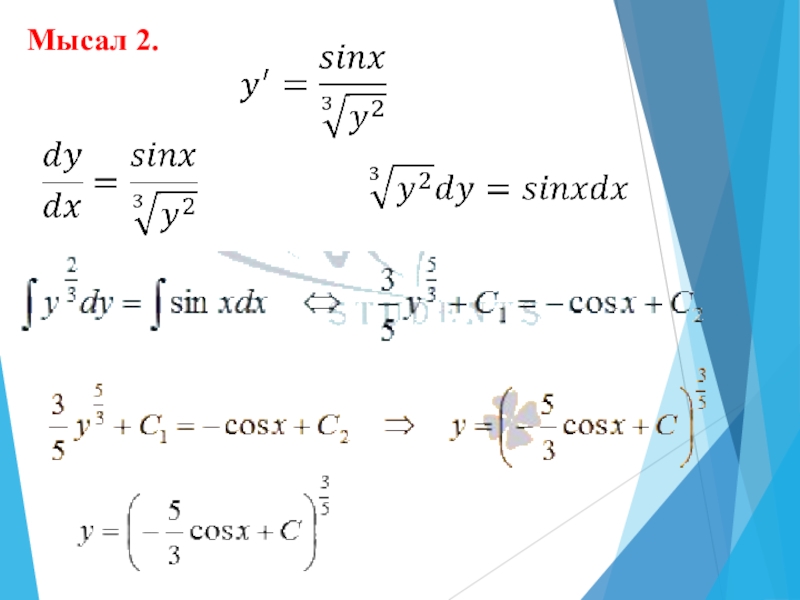- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад математика Дифференциал теңдеулер (11 сынып)
Содержание
- 1. Презентация математика Дифференциал теңдеулер (11 сынып)
- 2. Дифференциал теңдеу ұғымын және анықтамасын, дифференциалдық теңдеудің
- 3. Оқу мақсаттары
- 4. Интегралдар кестесі. Дербес жағдайда: Дербес жағдайда :
- 5. Дербес жағдайда :Дербес жағдайда :
- 6. 1.Келесі функциялардың берілген аралықтардағы алғашқы функциясын табыңыз:Қайталаймыз.
- 7. Слайд 7
- 8. Табиғаттағы көптеген құбылыстар дифференциалдық теңдеулер деп аталатын
- 9. Дифференциалдық теңдеулерге келтірілетін есептерДифференциалдық теңдеулер мысалын қарастырайық.
- 10. 2. Радиактивті ыдырау.Эксперимент арқылы заттың радиоактивті ыдырау
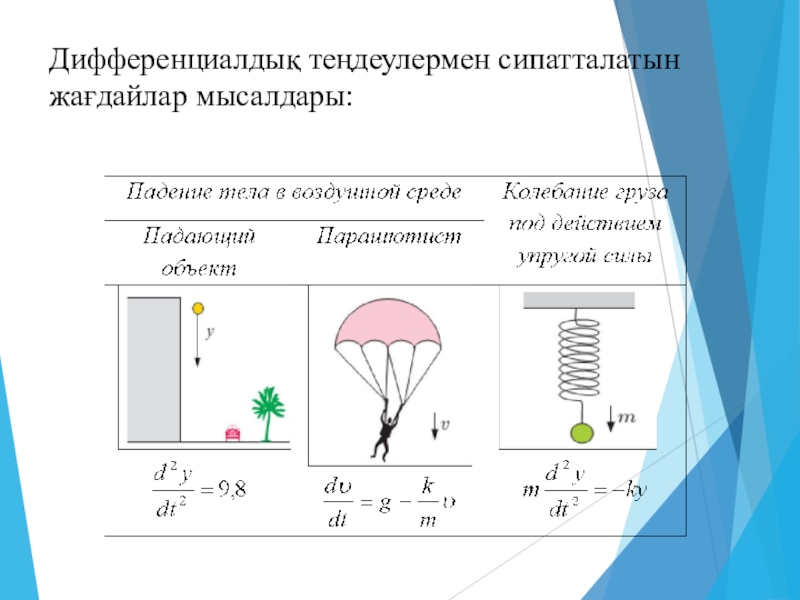
- 11. Дифференциалдық теңдеулермен сипатталатын жағдайлар мысалдары:
- 12. Дифференциалдық теңдеулер мысалдары:
- 13. АнықтамаДифференциалдық теңдеудің реті деп, құрамына кіретін ізделінді
- 14. АнықтамаДифференциалдық теңдеудің шешімі деп, теңдеуге қойғанда оны
- 15. . Геометриялық түрде жалпы шешім интегралдық қисықтар жиынтығын құрайды.
- 16. ТапсырмаТеңдеудің ретін анықтаңдар: функциясы теңдеуінің шешімі болатындығын тексеріңдер
- 17. АнықтамаБірінші ретті дифференциалдық теңдеудің жалпы шешімі деп,
- 18. Айнымалылары бөліктенетін теңдеулер
- 19. M (x) dx + Q(y) dy =
- 20. ..Мысал. ДТ шешіңіз:y’х-у = 0. или у
- 21. Мысал 2.
Дифференциал теңдеу ұғымын және анықтамасын, дифференциалдық теңдеудің ретін, жалпы және дербес шешімін, айнымалылары бөліктенетін теңдеулерді шешу туралы жалпы мағлұмат енгізу.Дифференциал теңдеулерге келтірілетін есептер қарастыру.Сабақ мақсаты:
Слайд 1Дифференциалдық теңдеулер.
ДТ жалпы және дербес шешімдері.
Дифференциалдық теңдеулерге келтірілетін есептер.
Слайд 2Дифференциал теңдеу ұғымын және анықтамасын, дифференциалдық теңдеудің ретін, жалпы және дербес
шешімін, айнымалылары бөліктенетін теңдеулерді шешу туралы жалпы мағлұмат енгізу.
Дифференциал теңдеулерге келтірілетін есептер қарастыру.
Дифференциал теңдеулерге келтірілетін есептер қарастыру.
Сабақ мақсаты:
Слайд 8Табиғаттағы көптеген құбылыстар дифференциалдық теңдеулер деп аталатын арнайы теңдеулермен сипатталады.
Анықтама.
Дифференциалдық
теңдеу деп, тәуелсіз айнымалы х –ты берілген
функциясымен және оның туындысымен байланыстыратын теңдеуді айтамыз, яғни
функциясымен және оның туындысымен байланыстыратын теңдеуді айтамыз, яғни
түрдегі теңдеу
Слайд 9Дифференциалдық теңдеулерге келтірілетін есептер
Дифференциалдық теңдеулер мысалын қарастырайық.
Слайд 102. Радиактивті ыдырау.
Эксперимент арқылы заттың радиоактивті ыдырау жылдамдығы оның бастапқы мөлшеріне
пропорционал болатындығы анықталған. Осы заңдылыққа сүйене отырып, радиоактивті ыдырау жөніндегі көптеген есептерді шешуге болады. Айталық, m(t) өрнегімен t уақытындағы радиоактивті заттың мөлшерін (грамм) белгілейік. Онда
m’(t)=-λ m(t)
теңдігі орындалады. Мұнда λ>0 пропорционалдық коэффициент, «минус» таңбасы уақыт өтісімен радиоактивті зат мөлшерінің кемитіндігін білдіреді.
m’(t)=-λ m(t)
теңдігі орындалады. Мұнда λ>0 пропорционалдық коэффициент, «минус» таңбасы уақыт өтісімен радиоактивті зат мөлшерінің кемитіндігін білдіреді.
Слайд 13Анықтама
Дифференциалдық теңдеудің реті деп, құрамына кіретін ізделінді функцияның ең жоғарғы туындысының
ретін айтады.
Бірінші ретті дифференциалдық теңдеудің жалпы түрі:
Бірінші ретті дифференциалдық теңдеудің жалпы түрі:
Слайд 14Анықтама
Дифференциалдық теңдеудің шешімі деп, теңдеуге қойғанда оны дұрыс теңдікке айналдыратын қандай
да бір функцияны айтамыз.
Дифференциалдық теңдеудің шешімінің графигі осы теңдеудің интегралдық қисығы деп аталады.
Дифференциалдық теңдеудің шешімінің графигі осы теңдеудің интегралдық қисығы деп аталады.
Слайд 17Анықтама
Бірінші ретті дифференциалдық теңдеудің жалпы шешімі деп, келесі функцияны айтамыз
Бірінші ретті
дифференциалдық теңдеудің дербес шешімі деп, кездейсоқ С тұрақтысының қандай да бір нақты мәнінде жалпы шешімнен алынатын шешімді айтады.
Слайд 19M (x) dx + Q(y) dy = 0 теңдеуі
мұнда dx
–тің алдындағы тек қана x –тен тәуелді, ал dy – тек қана y – тен тәуелді. Мұндай түрдегі теңдеулер айнымалылары бөліктенетін теңдеулер деп аталады.
Айнымалылары бөліктенетін теңдеулердің жалпы түрі келесі түрде сипатталады:
M (x) N(y) dx + P (x) Q(y) dy = 0
немесе
y’ = f(x) p(y)
Айнымалылары бөліктенетін теңдеулердің жалпы түрі келесі түрде сипатталады:
M (x) N(y) dx + P (x) Q(y) dy = 0
немесе
y’ = f(x) p(y)