на котором она написана,
и этот язык – математика”.
Г. Галилей
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Тригонометрия в нашей жизни
Содержание
- 1. Презентация к уроку Тригонометрия в нашей жизни
- 2. Задача № 1
- 3. Задача № 1Оцените свою работу
- 4. Задача № 2
- 5. Задача № 2Оцените свою работу
- 6. Задача № 3
- 7. Задача № 3Оцените свою работу
- 8. Тригонометриятреугольник измеряюТермин ввел в употребление в 1595
- 9. Тема урокаЦель урока …Тригонометрия в нашей жизни
- 10. Исследование:2. Изучение теории, посвященной данной проблематике1. Постановка проблемы3. Выдвижение гипотезы4. Доказательство гипотезы5. Вывод
- 11. 1. ПроблемаПочему знания тригонометрии необходимы для современного человека?История развития тригонометрии2. Изучение теории, посвященной данной проблематике
- 12. Слайд 12
- 13. Древний Вавилон
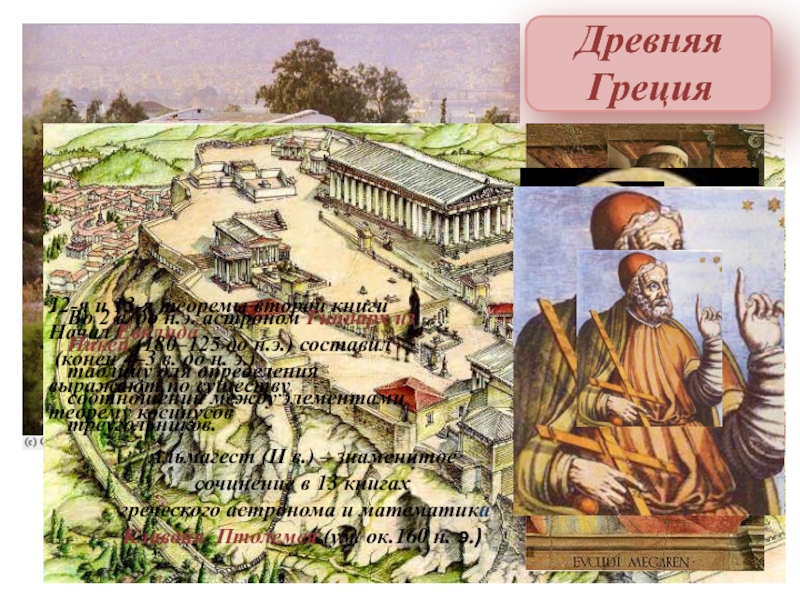
- 14. 12-я и 13-я теоремы второй книги Начал
- 15. Древняя ИндияЕсли греки по углам вычисляли
- 16. Термины «синус» и
- 17. Арабские ученыеАль-Баттани (ок. 900 н.э.) в
- 18. Европейские математикиИоганн Мюллер – Региомонтан (перевод
- 19. Николай Коперник1473 - 1543Тихо Браге1546 - 1601Иоганн Кеплер1571 - 1630Европейские математики
- 20. Европейские математикиДополнил и систематизировал различные случаи
- 21. Европейские математикиЧлен Российской академии наук Леонард
- 22. 3. Выдвижение гипотезыЗакономерности физических явлений природы, физиологических
- 23. Задача 4Жестянщику надо изготовить колено цилиндрической водосточной
- 24. 4. Доказательство1. Используя материалы укажите области применения
- 25. Над какой темой мы сегодня работали?Какую цель
- 26. Сегодня на уроке я…НаучилсяУзнал
- 27. Домашнее заданиеРешу ЕГЭ Вариант № 8632586выполнить до 4 декабря
Задача № 1
Слайд 8Тригонометрия
треугольник
измеряю
Термин ввел в употребление в 1595 немецкий математик
и богослов
Варфоломей Питиск, автор тригонометрических таблиц и учебника по тригонометрии.
Слайд 10Исследование:
2. Изучение теории, посвященной данной проблематике
1. Постановка проблемы
3. Выдвижение гипотезы
4. Доказательство
гипотезы
5. Вывод
Слайд 111. Проблема
Почему знания тригонометрии
необходимы для современного человека?
История развития тригонометрии
2. Изучение
теории, посвященной данной проблематике
Слайд 1412-я и 13-я теоремы второй книги Начал Евклида
(конец 4–3 в.
до н. э.)
выражают по существу
теорему косинусов
выражают по существу
теорему косинусов
Древняя Греция
Во 2 в. до н.э. астроном Гиппарх из Никеи (180–125 до н.э.) составил таблицу для определения соотношений между элементами треугольников.
Альмагест (II в.) – знаменитое сочинение в 13 книгах
греческого астронома и математика Клавдия Птолемея (ум. ок.160 н. э.)
Слайд 15Древняя Индия
Если греки по углам вычисляли хорды, то индийские астрономы
в сочинениях 4–5 вв. перешли к полухордам двойной дуги, т.е. в точности к линиям синуса
Слайд 16
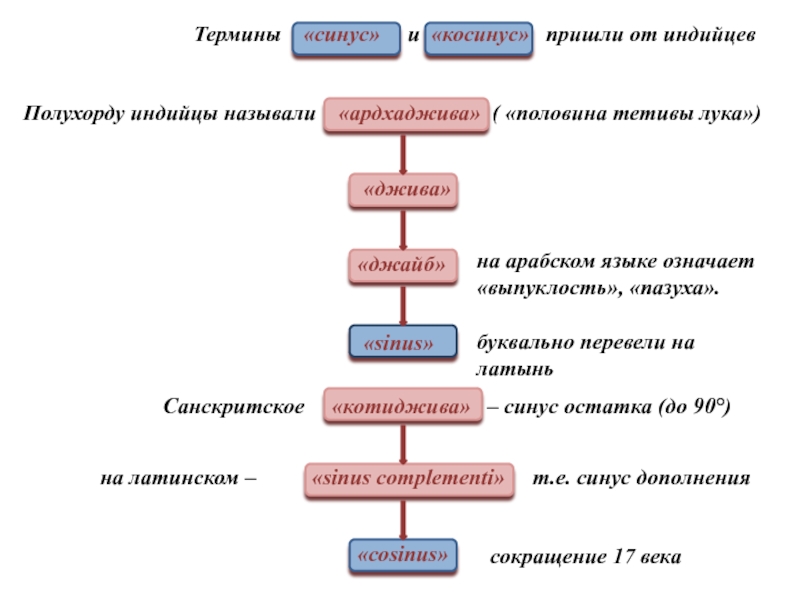
Термины «синус» и «косинус» пришли от
индийцев
Полухорду индийцы называли «ардхаджива» ( «половина тетивы лука»)
«джива»
«джайб»
на арабском языке означает «выпуклость», «пазуха».
«sinus»
буквально перевели на латынь
Санскритское «котиджива» – синус остатка (до 90°)
на латинском – «sinus complementi» т.е. синус дополнения
«cosinus»
сокращение 17 века
Слайд 17Арабские ученые
Аль-Баттани (ок. 900 н.э.)
в математической части
«Сабейского зиджа»
описал методы вычисления
сферических треугольников
Мухаммед из Буджана
(Абу-ль-Вефа)
940–997 гг.
присоединил к линиям синусов и косинусов линии тангенсов, котангенсов
Особенно большое влияние на развитие тригонометрии оказал «Трактат о полном четырехстороннике»
астронома
Насир-эд-Дин из Туса (ат-Туси)
(1201–1274).
Это было первое в мире сочинение, в котором тригонометрия трактовалась как самостоятельная область математики.
Слайд 18Европейские математики
Иоганн Мюллер – Региомонтан
(перевод на латинский названия родного
города Кенигсберга)
(1436–1476)
«О треугольниках всех родов пять книг».
Впервые отступил от шестидесятиричного
деления радиуса и за единицу измерения
линии синуса
принял одну десятимиллионную часть радиуса.
(1436–1476)
«О треугольниках всех родов пять книг».
Впервые отступил от шестидесятиричного
деления радиуса и за единицу измерения
линии синуса
принял одну десятимиллионную часть радиуса.
Региомонтан
(1436–1476)
Георг Лаухен (Ретик)
1514-1574
единственный ученик Коперника
30 лет работал над тригонометрическими таблицами ( углы через 10,,)
Синусы имели пятнадцать значащих цифр
Георг Лаухен (Ретик)
1514-1574
Слайд 19Николай Коперник
1473 - 1543
Тихо Браге
1546 - 1601
Иоганн Кеплер
1571 - 1630
Европейские
математики
Слайд 20Европейские математики
Дополнил и систематизировал различные случаи решения плоских и сферических
треугольников, открыл «плоскую» терему косинусов и
формулы для тригонометрических функций кратных углов
формулы для тригонометрических функций кратных углов
Франсуа Виет
(1540 - 1603)
Исаак Ньютон
(1643 - 1727)
Разложил тригонометрические функции в ряды и открыл путь их использования в математическом анализе
Слайд 21Европейские математики
Член Российской академии наук
Леонард Эйлер
(1707 - 1783)
Эйлер
стал рассматривать значения тригонометрических функций как числа – величины тригонометрических линий в круге, радиус которого принят за единицу («тригонометрический круг» или «единичная окружность»).
вывел все тригонометрические формулы из нескольких основных
дал окончательное решение о знаках тригонометрических функций в разных четвертях
установил несколько неизвестных до него формул
ввел единообразные обозначения
Современный вид тригонометрия
получила именно в его трудах.
Слайд 223. Выдвижение гипотезы
Закономерности
физических явлений природы,
физиологических процессов
можно описать с
помощью тригонометрии
и тригонометрических функций.
и тригонометрических функций.
4. Доказательство
Слайд 23Задача 4
Жестянщику надо изготовить колено цилиндрической водосточной трубы диаметром D. Взяв
лист железа (без учета швов), он должен его разрезать. По какой линии нужно разрезать второй лист, чтобы соединить две трубы? Постройте эту линию.
Оцените свою работу
Слайд 244. Доказательство
1. Используя материалы укажите области применения тригонометрии.
Почему знания тригонометрии
необходимы
для современного человека?
2. Приведите примеры
3. Сделайте вывод
5. Вывод
Слайд 25Над какой темой мы сегодня работали?
Какую цель перед собой поставили?
Какие способы
использовали?
1. Постановка проблемы
2. Изучение теории
3. Выдвижение гипотезы
4. Доказательство гипотезы
5. Вывод
Исследование:
Слайд 26Сегодня на уроке я…
Научился
Узнал
Участвовал
Выдвигал гипотезу
Доказывал
Проводил исследования
Сделал модель
Узнал о методе
Работал
Выдвигал гипотезу
Доказывал
Проводил исследования
Сделал модель
Узнал о методе
Работал
