обл.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии для учащихся 10 класса по теме Перпендикулярность прямой и плоскости
Содержание
- 1. Презентация к уроку геометрии для учащихся 10 класса по теме Перпендикулярность прямой и плоскости
- 2. Перпендикулярные прямые в пространствеПараллельные прямые, перпендикулярные к
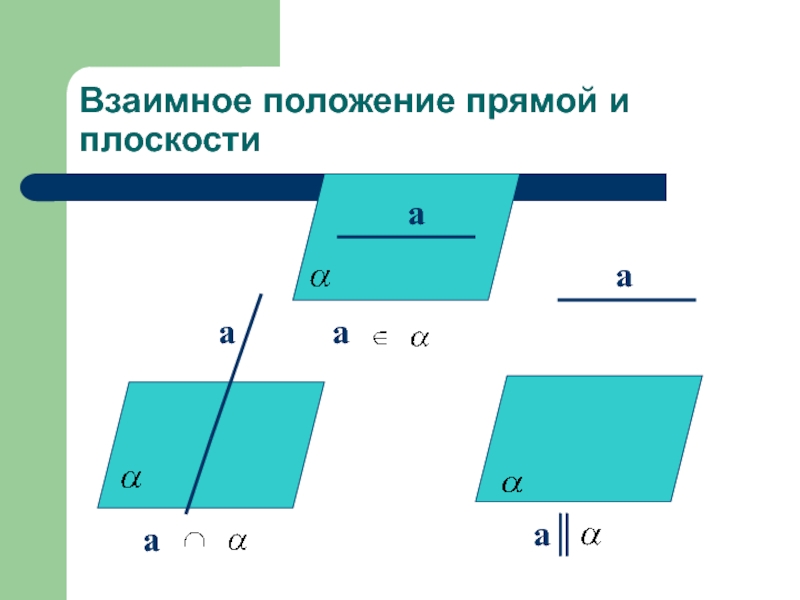
- 3. Взаимное положение прямой и плоскостиaa║aaaa
- 4. Слайд 4
- 5. Лемма: Если одна из двух параллельных прямых
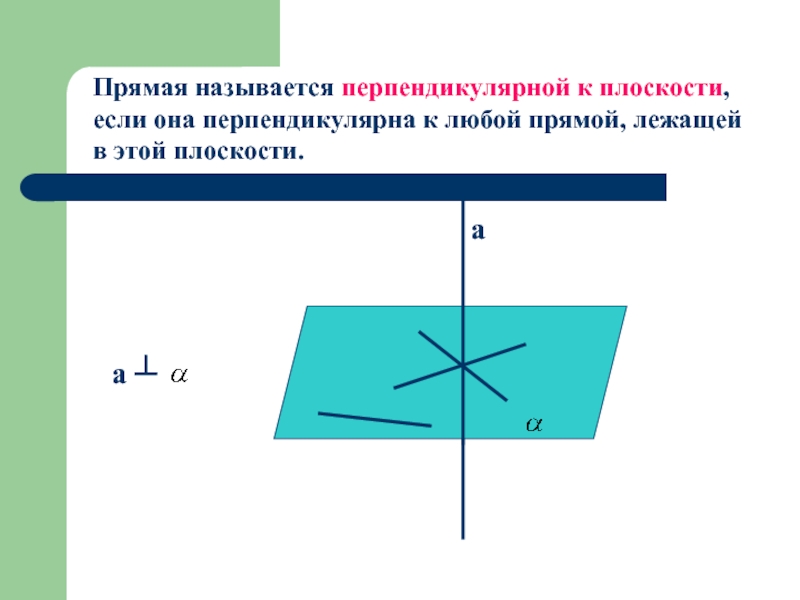
- 6. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.aа ┴
- 7. Слайд 7
- 8. аа1хТеорема: Если одна из двух параллельных прямых
- 9. Теорема: Если две прямые перпендикулярны к плоскости,
- 10. OLQPBApqmlaaТеорема:
- 11. .MabcТеорема о прямой, перпендикулярной к плоскости.Через любую
Перпендикулярные прямые в пространствеПараллельные прямые, перпендикулярные к плоскостиПризнак перпендикулярности прямой и плоскостиТеорема о прямой, перпендикулярной к плоскости
Слайд 1Перпендикулярность прямой и плоскости
Методическая разработка Губарь О.М.
МОУ «СОШ№11», г. Усть-Илимска, Иркутской
Слайд 2Перпендикулярные прямые в пространстве
Параллельные прямые, перпендикулярные к плоскости
Признак перпендикулярности прямой и
плоскости
Теорема о прямой, перпендикулярной к плоскости
Теорема о прямой, перпендикулярной к плоскости
Слайд 5Лемма: Если одна из двух параллельных прямых перпендикулярна к третьей прямой,
то и другая прямая перпендикулярна к этой прямой.
C
M
c
a
b
A
Дано: a║b; a┴с
Доказать: b┴c
Доказательство:
Проведем CM║c, MA║a.
Так как a┴с, то └AMC=90
a║b (по условию)
MA║a.(по построению)
}=>
MA║b, MC║c
MA┴MC
}=>
b┴c
Слайд 6
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой,
лежащей в этой плоскости.
a
а ┴
Слайд 8
а
а1
х
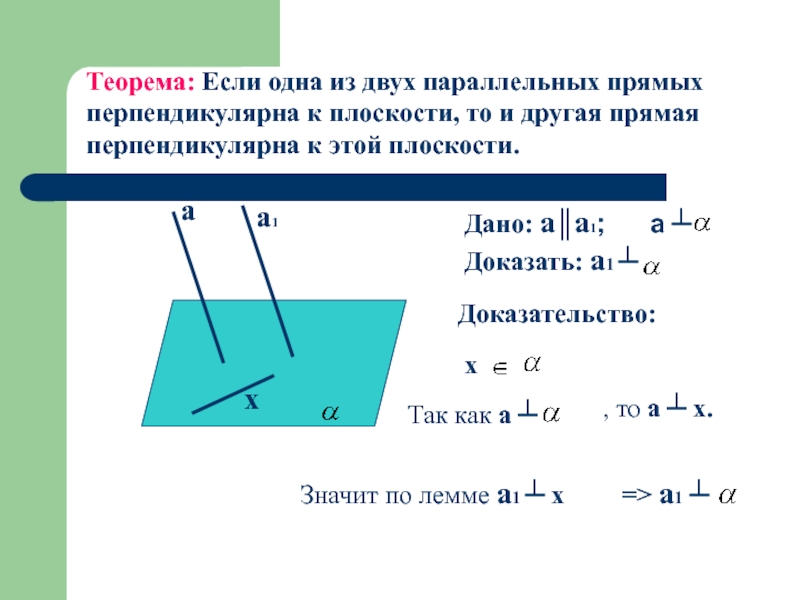
Теорема: Если одна из двух параллельных прямых перпендикулярна к плоскости, то
и другая прямая перпендикулярна к этой плоскости.
Доказательство:
Дано: a║а1; a ┴
Доказать: a1 ┴
x
Так как a ┴
, то a ┴ х.
Значит по лемме а1 ┴ х
=> a1 ┴
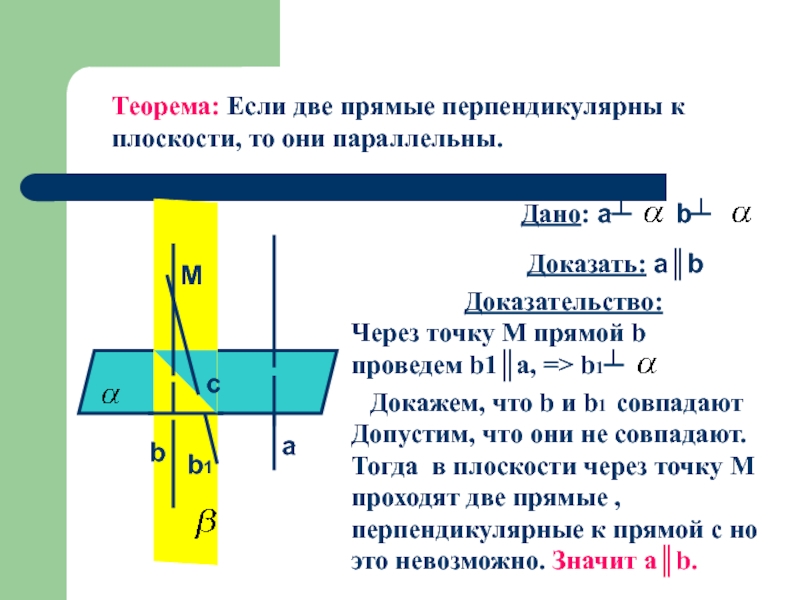
Слайд 9Теорема: Если две прямые перпендикулярны к плоскости, то они параллельны.
M
c
a
b
b1
Дано: a┴
b┴
Доказать: a║b
Доказательство:
Через точку М прямой b проведем b1║a, => b1┴
Докажем, что b и b1 совпадают
Допустим, что они не совпадают. Тогда в плоскости через точку М проходят две прямые , перпендикулярные к прямой с но это невозможно. Значит а║b.
Слайд 10
O
L
Q
P
B
A
p
q
m
l
a
a
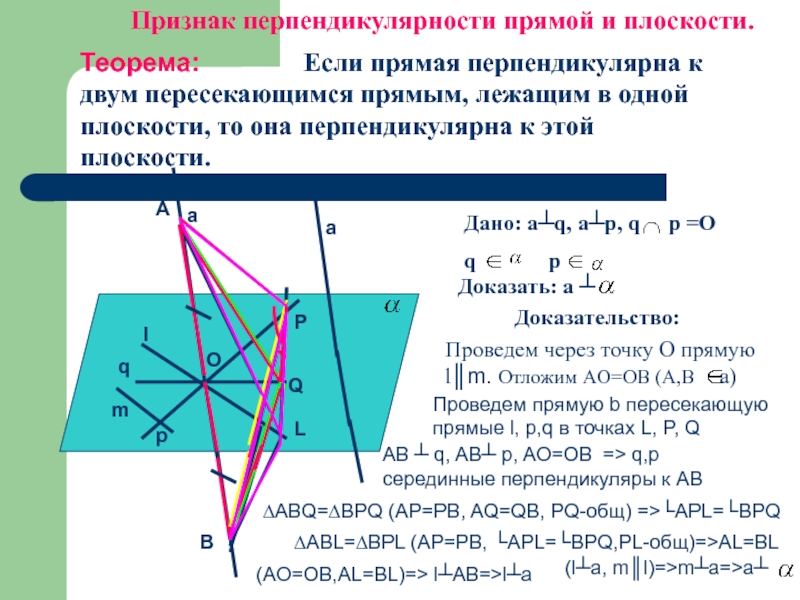
Теорема: Если прямая перпендикулярна к
двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости.
Дано: a┴q, a┴p, q p =O
q p
Доказать: a ┴
Доказательство:
Проведем через точку О прямую l║m. Отложим AO=OB (A,B a)
Проведем прямую b пересекающую прямые l, p,q в точках L, P, Q
AB ┴ q, AB┴ p, AO=OB => q,p серединные перпендикуляры к АВ
∆ABQ=∆BPQ (AP=PB, AQ=QB, PQ-общ) =>└APL=└BPQ
∆ABL=∆BPL (AP=PB, └APL=└BPQ,PL-общ)=>AL=BL
(AO=OB,AL=BL)=> l┴AB=>l┴a
(l┴a, m║l)=>m┴a=>a┴
Признак перпендикулярности прямой и плоскости.
Слайд 11
.
M
a
b
c
Теорема о прямой, перпендикулярной к плоскости.
Через любую точку пространства проходит прямая,
перпендикулярная к данной плоскости, и при том только одна.
Дано:
Доказать: M с, c┴
M,
Доказательство:
Проведем в плоскости прямую а и рассмотрим плоскость М ┴а.
∩
=b
В плоскости проведем прямую с┴b
с- искомая прямая
Предположим, что через точку М проходит еще одна прямая с1 ┴
Тогда с1║ с, это невозможно, так как с1∩ с = М
