- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроке алгебры 8 класс Тема: Решение систем линейных уравнений к учебнику Ю.М.Калягина и др.
Содержание
- 1. Презентация к уроке алгебры 8 класс Тема: Решение систем линейных уравнений к учебнику Ю.М.Калягина и др.
- 2. Содержание 1.Способ подстановки при решении систем
- 3. Способ подстановкиРассмотрим каждое уравнение в отдельности.Этот способ
- 4. Вернемся в систему:2) Полученное для y выражение подставим
- 5. 3) Выходим из системы и решаем уравнение с одной неизвестной:Возвращаемся в систему:.Способ подстановки
- 6. Способ сложения1) Выберем неизвестную (например x),уравняем коэффициенты при x умножением на соответствующие числа. Решить систему уравнений
- 7. Способ сложения2) Вычтем одно уравнение из другого.3) Решим полученное
- 8. Способ сложения5) Подставим найденное значение y в
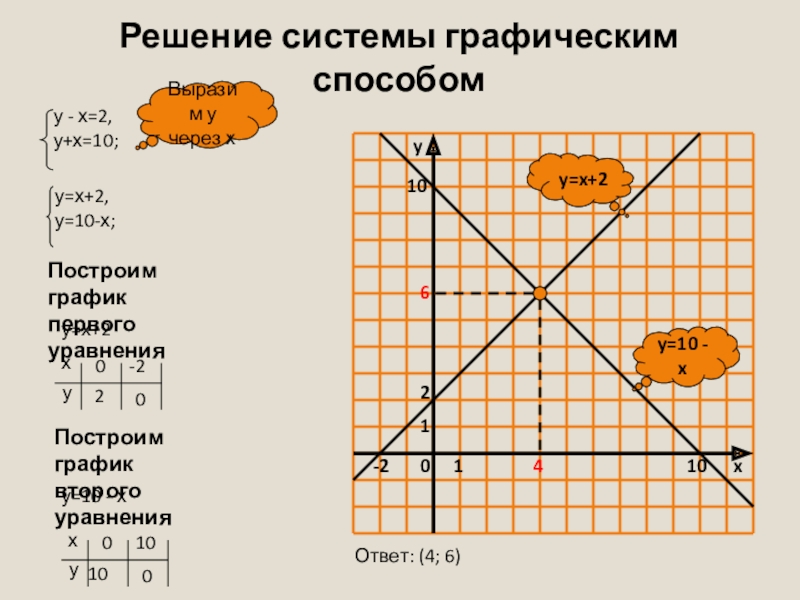
- 9. Решение системы графическим способомy=10 - xy=x+2Выразим учерез хПостроим графикпервого уравненияу=х+2Построим графиквторого уравненияу=10 - хОтвет: (4; 6)
- 10. Для графического решения системы нужно:Построить графики каждого
- 11. На плоскости возможны три случая взаимного расположения двух прямых ― графиков уравнений системы
- 12. Три случая взаимного расположения двух прямых 1. Прямые
- 13. Три случая взаимного расположения двух прямых2. Прямые
- 14. Три случая взаимного расположения двух прямых3. Прямые совпадают.Тогда система уравнений имеет бесконечно много решений.Например:
- 15. Перечень ссылок http://www.edu.ru/ http://festival.1september.ru/articles/529580 http://tvv48.narod.ru/it/contents.html http://en.edu.ru/db/sect/3217/3284 http://comp-science.narod.ru/ http://www.informika.ru/text/magaz/pedagog/title.html http://ito.edu.ru/index.html
Содержание 1.Способ подстановки при решении систем линейных уравнений 2. Способ сложения при решении систем линейных уравнений 3. Графический способ решения систем линейных уравнений
Слайд 1Решение систем линейных уравнений
Алгебра (7 класс)
Носова Надежда Васильевна
ГБОУ СОШ №593
Учитель математики
Слайд 2Содержание 1.Способ подстановки при решении систем линейных уравнений 2. Способ сложения при
решении систем линейных уравнений
3. Графический способ решения систем линейных уравнений
Слайд 3Способ подстановки
Рассмотрим каждое уравнение в отдельности.
Этот способ удобен тогда, когда хотя
бы один из коэффициентов при x или y равен 1 или -1.
Дана система уравнений
1) Выразим одно из неизвестных через другое неизвестное из любого уравнения.
Слайд 4Вернемся в систему:
2) Полученное для y выражение подставим вместо данной неизвестной во
второе уравнение.
Способ подстановки
Получилось уравнение с одной неизвестной
Слайд 53) Выходим из системы и решаем уравнение с одной неизвестной:
Возвращаемся в
систему:.
Способ подстановки
Слайд 6Способ сложения
1) Выберем неизвестную (например x),
уравняем коэффициенты при x умножением на соответствующие
числа.
Решить систему уравнений
Слайд 7Способ сложения
2) Вычтем одно уравнение из другого.
3) Решим полученное уравнение с одним неизвестным
4) Вернемся
в систему, записав одно из исходных уравнений и полученное значение y
Слайд 8Способ сложения
5) Подставим найденное значение y в первое уравнение, найдем вторую
неизвестную.
Тогда пара чисел (-3; 1) и будет решением системы.
Ответ:
Слайд 9Решение системы графическим способом
y=10 - x
y=x+2
Выразим у
через х
Построим график
первого уравнения
у=х+2
Построим график
второго
уравнения
у=10 - х
Ответ: (4; 6)
Слайд 10Для графического решения системы нужно:
Построить графики каждого из уравнений системы.
Найти координаты
точки пересечения построенных прямых (если они пересекаются)
Слайд 11 На плоскости возможны три случая взаимного расположения двух прямых ― графиков
уравнений системы
Слайд 12Три случая взаимного расположения двух прямых
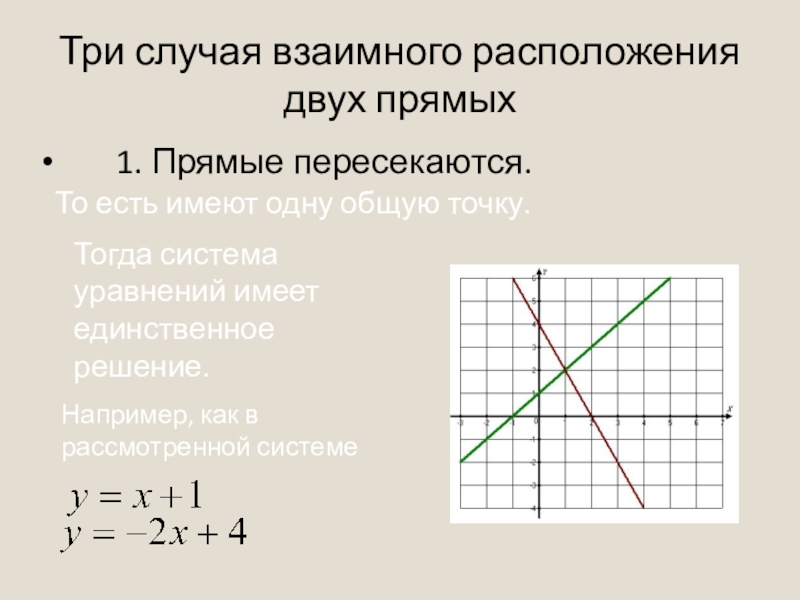
1. Прямые пересекаются.
То есть имеют одну
общую точку.
Тогда система уравнений имеет единственное решение.
Например, как в рассмотренной системе
Слайд 13Три случая взаимного расположения двух прямых
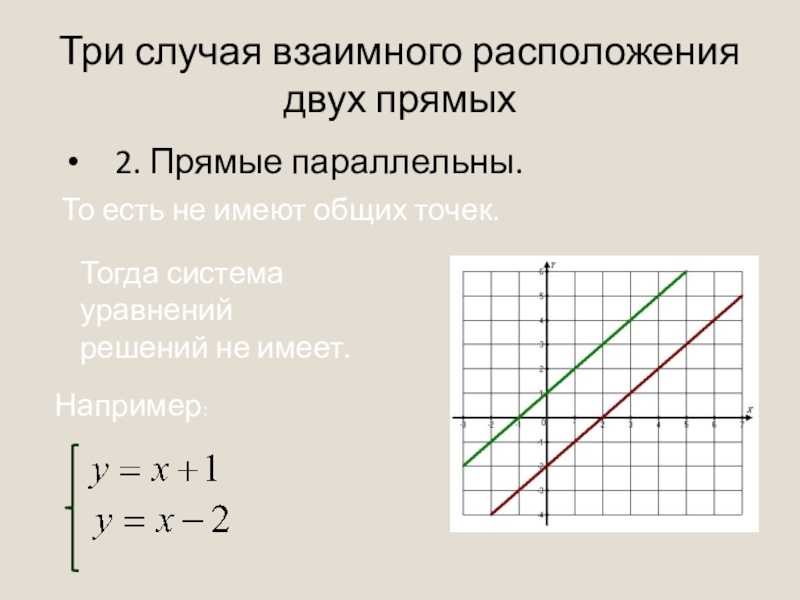
2. Прямые параллельны.
То есть не имеют
общих точек.
Тогда система уравнений решений не имеет.
Например:
Слайд 14Три случая взаимного расположения двух прямых
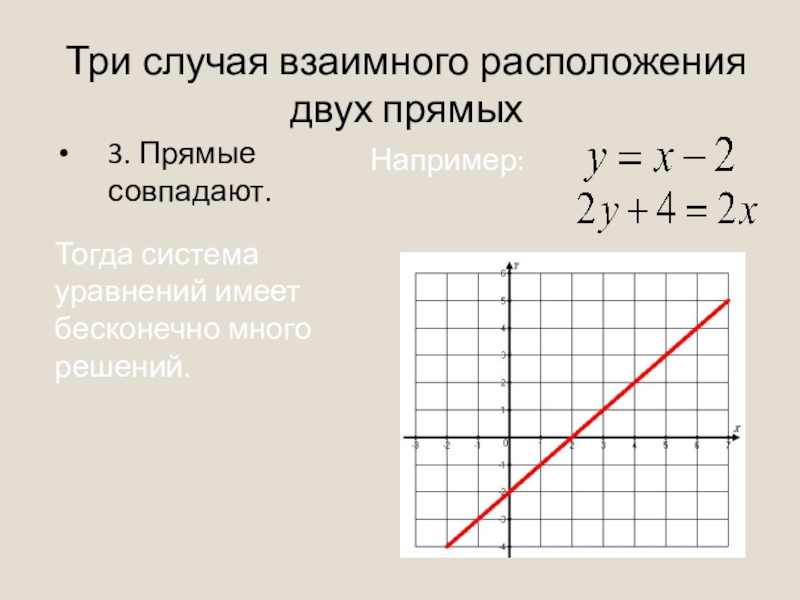
3. Прямые совпадают.
Тогда система уравнений имеет
бесконечно много решений.
Например:
Слайд 15
Перечень ссылок
http://www.edu.ru/
http://festival.1september.ru/articles/529580
http://tvv48.narod.ru/it/contents.html
http://en.edu.ru/db/sect/3217/3284
http://comp-science.narod.ru/
http://www.informika.ru/text/magaz/pedagog/title.html
http://ito.edu.ru/index.html
