Авторы проекта учащиеся 11 класса:
Перегудова Мария, Курдубина Алина.
Руководитель:
учитель математики Волкова Татьяна Валентиновна.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к исследовательскому проекту по математике Логарифмы вокруг нас
Содержание
- 1. Презентация к исследовательскому проекту по математике Логарифмы вокруг нас
- 2. Испокон веков люди пытались упростить вычисления: составляли
- 3. ЦЕЛИ И ЗАДАЧИ ПРОЕКТА: Цель
- 4. ОСНОВОПОЛАГАЮЩИЙ ВОПРОС:Возможна ли жизнь без логарифмов?
- 5. 1. Как давно люди знают о
- 6. Этапы работы над проектом1 этап.Подготовительный или погружение
- 7. повышенным интересом к математике; знаниями широты применения
- 8. ИСТОРИЯ ЛОГАРИФМОВ
- 9. Изобретение логарифмов Принцип, лежащий в основе любой
- 10. и через десять лет швейцарским механиком Бюрги (1552-1632).
- 11. ТерминТермин "логарифм" (logarithmus) принадлежит Неперу. Он возник
- 12. Десятичные логарифмыВ 1615 году в беседе с
- 13. Натуральный логарифмТермин "натуральный логарифм" ввели Менголи в
- 14. Таблицы логарифмовДжон Непер в 1590-х годах пришел
- 15. таблицы логарифмов На русском языке первые
- 16. В 1623 г. английский
- 17. Логарифмические линейки были двух видов. Первые выглядели
- 18. Для своего времени логарифмическая линейка была очень
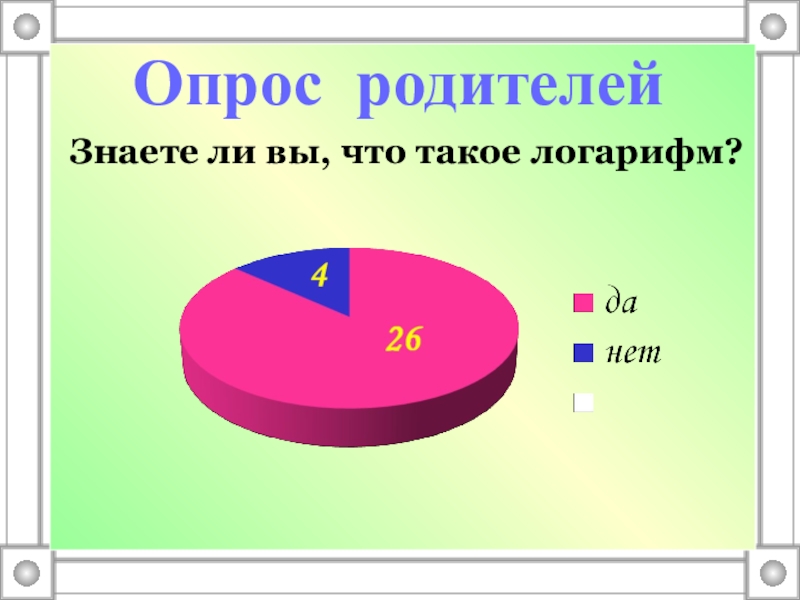
- 19. Знаете ли вы, что такое логарифм?Опрос родителей
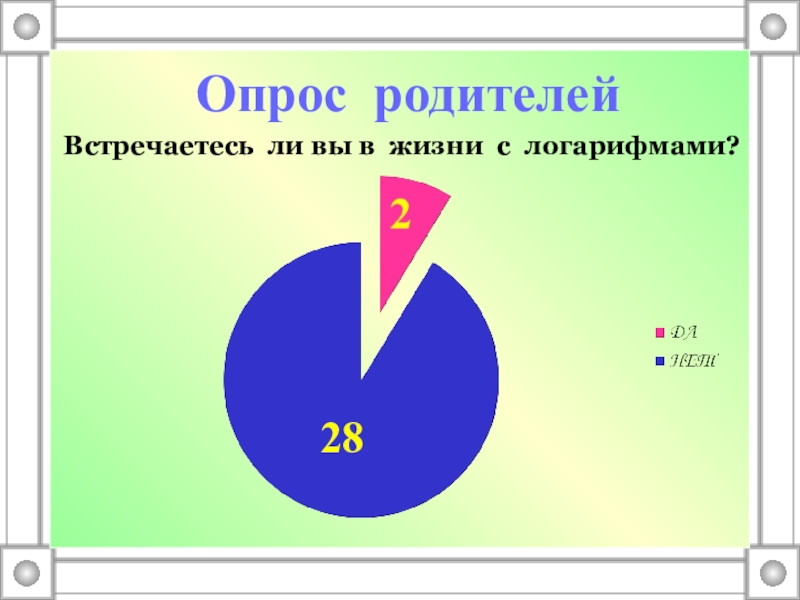
- 20. Опрос родителейВстречаетесь ли вы в жизни с логарифмами?28
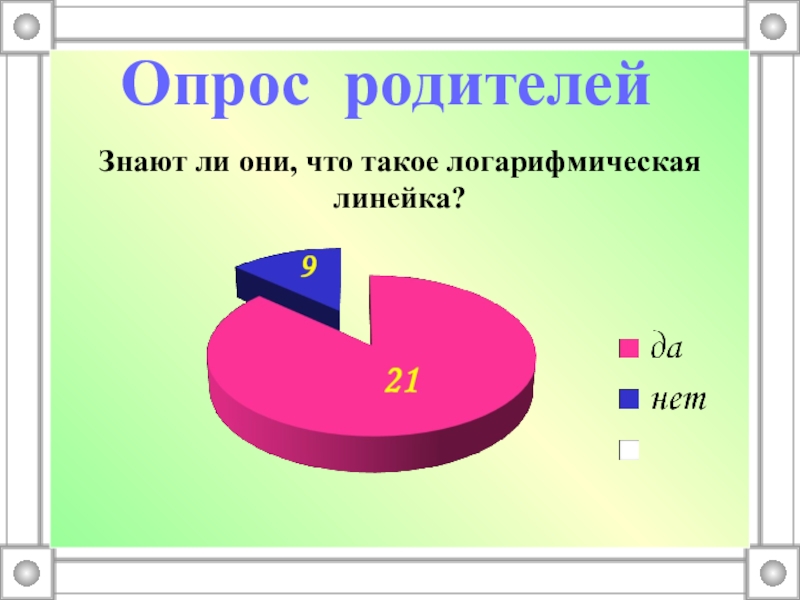
- 21. Знают ли они, что такое логарифмическая линейка?Опрос родителей
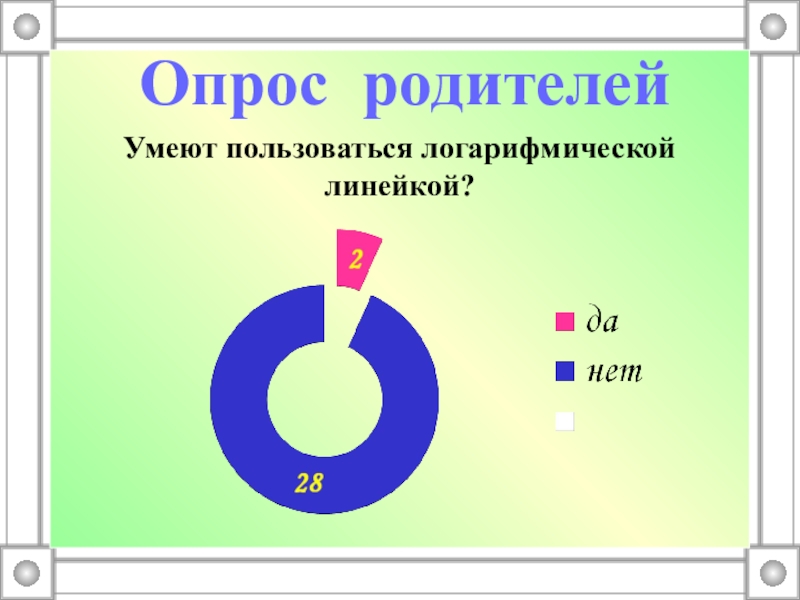
- 22. Опрос родителейУмеют пользоваться логарифмической линейкой?
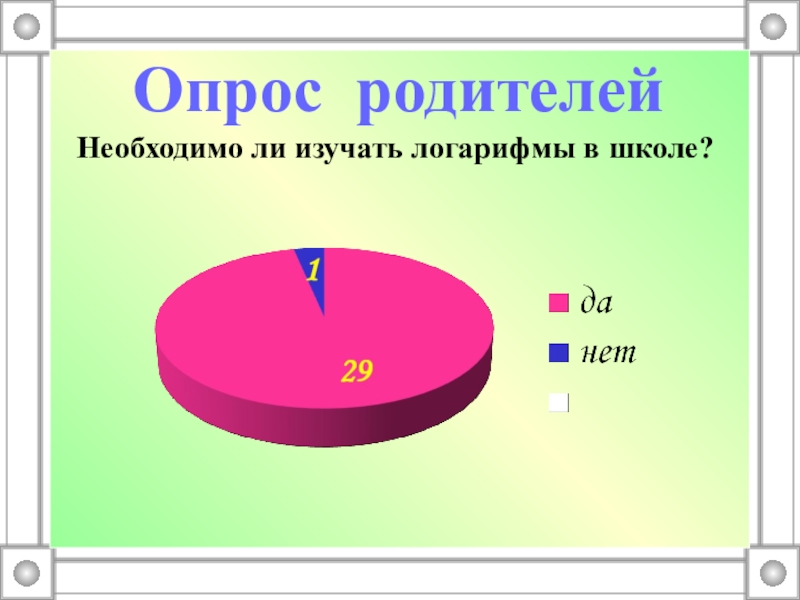
- 23. Опрос родителейНеобходимо ли изучать логарифмы в школе?
- 24. Ода экспонентеДве шкалы Гунтера – Вот чудо
- 25. Применение логарифмов
- 26. Для чего же нужны логарифмы в
- 27. По логарифмической шкале. Астрономы делят звезды по
- 28. Аналогично оценивается и громкость шума. Вредное влияние промышленных шумов на здоровье рабочих и производстве труда.Промышленность
- 29. Логарифмы в физикеЛогарифмы применяются для измерения энергетических
- 30. Единица громкости Единицей громкости
- 31. Частоту любого звука можно выразить формулой.N mn=n*2(
- 32. Эта формула, связывающая скорость ракеты с ее
- 33. Радиоактивный распадИзменение массы радиоактивного вещества происходит по
- 34. Коэффициент звукоизоляции стен измеряется по формуле
- 35. Изменение количества людей в стране
- 36. Логарифмическая спиральЛогарифмическую спираль является траекторией точки, которая
- 37. Раковины многих моллюсков, улиток, а так же
- 38. Один из наиболее распространенных пауков ЭПЕЙРА, сплетая
- 39. В технике часто применяют вращающиеся ножи. Сила,
- 40. Логарифмы в живописиЛогарифмические линии в природе замечают
- 41. По аналогии со спиралевидной закрученной раковине улитки у женщин существует прическа «улитка» из длинных волос.
- 42. Музыка. Теперь рассмотрим еще один интереснейший пример
- 43. Банковские расчеты В наше время нельзя представить
- 44. Используются логарифмы и в расчётах, связанных
- 45. Психология При оценке видимой яркости светил и
- 46. Логарифмические диковинки
- 47. Логарифмические диковинкиЛюбое число – тремя двойкамиЛюбое целое
- 48. Логарифмическая «комедия 2>3»
- 49. Слайд 49
- 50. ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА БАЙГРЕВА прибор, специально предназначенный для определения высоты и азимута светила по счислимой широте, известному склонению и часовому углу.
- 51. Логарифмическая Линейка (созвездие) — Лаг (Лот) (лат. Lochium Funis)
- 52. ПОДГОТОВКА К ЕГЭ
- 53. Задание 17 № 507646. Решите неравенство Решение.Левая
- 54. Решите неравенство: log2x(2x2-4x+6) ≤ log2x(x2+x).Решение. Ответ. (0; 0,5)U[2; 3].
- 55. Слайд 55
- 56. Слайд 56
- 57. Вывод:Многие природные явления не могли быть изучены
- 58. Логарифмы — это все! Музыка и звуки!И
- 59. ВЫВОД:Мы постарались проследить, как в ходе истории
- 60. С результатами работы мы выступили: перед учениками
- 61. Использованная литература1.Виленкин Н.Я. Алгебра и математический
- 62. СПАСИБО ЗА ВНИМАНИЕ
Слайд 1
Логарифмы вокруг нас
ИССЛЕДОВАТЕЛЬСКИЙ ПРОЕКТ ПО МАТЕМАТИКЕ
МБОУ Жирновская СОШ
2015
Слайд 2Испокон веков люди пытались упростить вычисления: составляли таблицы, вводили приближенные формулы,
Также нас заинтересовал вопрос: а можно ли встретить логарифмы в нашей жизни?
С учетом этого и была выбрана тема исследовательского проекта: «Логарифмы вокруг нас». Этот проект позволит нам по-новому взглянуть на окружающий нас мир, увидеть логарифмы в событиях, которые происходят на протяжении всей жизни и всей человеческой истории. Ведь логарифмы мы считаем можно встретить не только в математике, но и
в окружающем нас мире.
Актуальность темы
Слайд 3
ЦЕЛИ И ЗАДАЧИ ПРОЕКТА:
Цель проекта:
Создание
Задачи проекта:
Проект предполагает сбор и анализ данных, их представление в четком визуальном виде. Он направлен на формирование понимания содержательного смысла термина «логарифм».
1. Установить картину возникновения понятия «логарифм» и выявить примеры их применения.
2. Сформировать умения производить вычисления, необходимые для применения в практической деятельности и ЕГЭ;
3. Выявить и изучить области, в которых применяются логарифмы.
Слайд 5
1. Как давно люди знают о логарифмах?
2. Как логарифмы
3. Как часто люди в жизни сталкиваются с логарифмами?
4. Применение логарифмов на ЕГЭ по математике?
Проблемные вопросы:
Слайд 6Этапы работы над проектом
1 этап.
Подготовительный или погружение в тему.
Формулирование темы,
вопросов.
Определение темы проекта, выдвижение гипотез.
2 этап
Реализация проекта.
Сбор и обработка информации. Создание презентаций.
3 этап
Защита проекта.
Представление презентаций, выступление на конференции.
Слайд 7
повышенным интересом к математике;
знаниями широты применения логарифмов в жизни;
умением
умением использовать приемы, рационализирующие вычисления;
умением находить и работать с дополнительной информацией.
необходимыми знаниями для ЕГЭ.
В результате работы над проектом обучающиеся овладеют:
Слайд 9
Изобретение логарифмов
Принцип, лежащий в основе любой системы логарифмов, известен очень
Слайд 11
Термин
Термин "логарифм" (logarithmus) принадлежит Неперу.
Он возник из сочетания греческих слов:
которое означало "число отношений".
log
Слайд 12
Десятичные логарифмы
В 1615 году в беседе с профессором математики Генри Бригсом
Так появились десятичные логарифмы и были
напечатаны первые логарифмические таблицы.
lg
Слайд 13
Натуральный логарифм
Термин "натуральный логарифм" ввели Менголи в 1659 г. и вслед
ln
Слайд 14
Таблицы логарифмов
Джон Непер в 1590-х годах пришел к идее логарифмических вычислений
и составил первые таблицы логарифмов, однако свой знаменитый
“Описание удивительных таблиц логарифмов” опубликовал лишь в 1614 году.
Слайд 15
таблицы логарифмов
На русском языке первые логарифмические таблицы
Но во всех логарифмических таблицах были допущены ошибки при вычислении. Первые безошибочные таблицы вышли в 1857 году в Берлине в обработке немецкого математика К. Бремикера
Слайд 16
В 1623 г. английский математик Д. Гунтер изобрёл первую логарифмическую линейку,
Логарифмическая линейка
Слайд 17
Логарифмические линейки были двух видов. Первые выглядели такими, как и представленная
Слайд 18
Для своего времени логарифмическая линейка была очень нужным инструментом. Она позволяла
При помощи таких логарифмических линеек советские инженеры выполняли расчеты при проектировании зданий, сооружений, крупных промышленных объектов, возводимых в СССР, новых самолетов, машин, кораблей. Ее использовали бухгалтеры и специалисты, которых сейчас назвали бы менеджерами. Когда-то логарифмические линейки значительно облегчали жизнь и студентам.
Ныне неумолимый прогресс предал логарифмические линейки забвению и оставил им место только на музейной полке.
Слайд 24
Ода экспоненте
Две шкалы Гунтера –
Вот чудо изобретательности.
Экспонентой порождена
Логарифмическая линейка:
У
Инструмента полезнее, чем она.
Даже изящные искусства питаются ею.
Разве музыкальная гамма не есть
Набор передовых логарифмов?
Английский поэт Э.Брилл
Слайд 26
Для чего же нужны логарифмы в химии и как они применяются?
Думаю,
Водородным показателем pH называется отрицательный десятичный логарифм концентрации ионов водорода.
Переводя на доступный язык, можно сказать, что с помощью водородного показателя определяется уровень кислотности среды.
С помощью логарифмов ученые научились определять точный возраст ископаемых пород и животных. Наиболее распространен Радиоуглеродный анализ.
Логарифмы в химии и биофизике
Слайд 27
По логарифмической шкале. Астрономы делят звезды по степени яркости на видимые
Астрономия
Слайд 28
Аналогично оценивается и громкость шума. Вредное влияние промышленных шумов на здоровье
Промышленность
Слайд 29
Логарифмы в физике
Логарифмы применяются для измерения энергетических (мощность, энергия) или силовых
ДЕЦИБЕЛ - десятая часть бела, безразмерной единицы для измерения отношения некоторых величин (например, энергетических — мощности и энергии или силовых — напряжения и силы тока) по логарифмической шкале.
Шкала звуковой мощности
Исходя из полученных значений, Белл определил шкалу звуковой мощности от 0 до 13. Ощущение громкости базируется на логарифмической шкале уровня мощности, Преобразование между мощностью и громкостью по шкале Белла выглядит следующим образом: громкость (в белах) = lg(P1/P0), где P0 - порог слышимости звука.
Уровень звукового давления
(англ. SPL, Sound Pressure Level) — измеренное по относительной шкале значение звукового давления, отнесённое к опорному давлению = 20 мкПа, соответствующему порогу слышимости синусоидальной звуковой волны частотой 1 кГц: дБ.
Слайд 30
Единица громкости
Единицей громкости служит «бел», практически -
Физическая же сила этих шумов (точнее - энергия) составляет прогрессию геометрическую со знаменателем 10. Разности громкостей в 1 бел отвечает отношение силы шумов 10. Значит, громкость шума выраженная в белах, равна десятичному логарифму его физической силы.
Слайд 31
Частоту любого звука можно выразить формулой.
N mn=n*2( 12v2)p
Логарифмируя эту формулу. Получаем
lg Nmp= lg n + m lg2 + p(lg2)/12,
lg Nmp = lg n +(m+p/12)lg2
Принимая частоту самого низкого «до» за единицу (n=1) и приводя все логарифмы к основанию 2.имеем log2N=m+p/12
Слайд 32
Эта формула, связывающая скорость ракеты с ее массой m:
где Vr – скорость вылетающих газов, m0 – стартовая масса ракеты. Скорость истечения газа при сгорании топлива Vr невелика (в настоящее время она меньше или равна 2км/с). Логарифм растет очень медленно, и для того чтобы достичь космической скорости,
необходимо сделать большим отношение ,
т.е. почти всю стартовую массу отдать под топливо.
Формула Циолковского.
Слайд 33
Радиоактивный распад
Изменение массы радиоактивного вещества происходит по формуле
,
T -
Это означает, что через время Т после начального момента времени, масса радиоактивного вещества уменьшается вдвое.
Слайд 34
Коэффициент звукоизоляции стен измеряется по формуле
где p0 – давление звука до
Звукоизоляция стен.
Слайд 35
Изменение количества людей в стране на небольшом отрезке времени
где N0 – число людей при t=0, N – число людей в момент t, λ – некоторая константа.
Народонаселение.
Слайд 36
Логарифмическая спираль
Логарифмическую спираль является траекторией точки, которая движется вдоль равномерно вращающейся
Первым учёным, открывшим эту удивительную кривую, был Р. Декарт
Слайд 37
Раковины многих моллюсков, улиток, а так же рога горных козлов закручены
Слайд 38
Один из наиболее распространенных пауков ЭПЕЙРА, сплетая паутину, закручивает нити вокруг
По логарифмическим спиралям закручены и многие галактики, в частности, галактика которой принадлежит Солнечная Система.
Слайд 39
В технике часто применяют вращающиеся ножи. Сила, с которой они давят
В технике
Слайд 40
Логарифмы в живописи
Логарифмические линии в природе замечают не только математики, но
“…моей навязчивой идеей, настоящей маниакальной страстью, стала картина Я. Вермера “Кружевница”, репродукция которой висела в отцовском кабинете”
Сальвадор Дали
«Кружевница», Ян Вермер
Слайд 41
По аналогии со спиралевидной закрученной раковине улитки у женщин существует прическа
Слайд 42
Музыка.
Теперь рассмотрим еще один интереснейший пример о связи логарифмов и
Слайд 43
Банковские расчеты
В наше время нельзя представить экономику банковского дела без
Итак, в нашем случае деньги на вкладе накапливаются по формуле
Нам необходимо решить уравнение
Мы можем решить это уравнение по определению логарифма числа. Вычислим этот логарифм, предварительно перейдя к основанию 10, пользуясь калькулятором.
Таким образом, удвоение вклада произойдет через 6 лет (с небольшим).
Слайд 44
Используются логарифмы и в расчётах, связанных с изменением атмосферного
Высота над уровнем моря вычисляется по формуле h=(8000/0,4343)lg(p0 /p), где p0 =760 мм рт.ст., р - давление на высоте h м.
Давление в п. Жирнов на 25 марта 2015 года равно 738 мм рт. ст. Вычислим, на какой высоте находится наш поселок.
Решение. Найдем высоту, на которой находится наш поселок:
h=(8000/0,4343)lg(760/738) ≈235 м
Ответ: 235м.
ГЕОГРАФИЯ
Слайд 45
Психология
При оценке видимой яркости светил и при измерении громкости шума,
Слайд 47
Логарифмические диковинки
Любое число – тремя двойками
Любое целое положительное число изобразить с
Слайд 49
Логарифмические линейки
Однако в начале 21 века логарифмические линейки получили второе рождение в наручных часах: следуя моде, производители некоторых марок (среди которых BreitlingОднако в начале 21 века логарифмические линейки получили второе рождение в наручных часах: следуя моде, производители некоторых марок (среди которых Breitling, CitizenОднако в начале 21 века логарифмические линейки получили второе рождение в наручных часах: следуя моде, производители некоторых марок (среди которых Breitling, Citizen, Orient) выпустили модели со встроенной логарифмической линейкой, выполненной в виде вращающихся колец со шкалами вокруг циферблата. Производители обычно называют такие устройства «навигационная линейка». Их достоинство — можно сразу, в отличие от микрокалькулятора, получить информацию, соответствующую табличной форме представления (например, таблицу расхода топлива на пройденное расстояние, перевода миль в километры и тому подобное). Однако, в большинстве случаев логарифмические линейки, встроенные в часы, не оснащены шкалами для вычисления значений тригонометрических функций.
Слайд 50
ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА БАЙГРЕВА
прибор, специально предназначенный для определения высоты и азимута светила по счислимой широте, известному склонению и часовому углу.
Слайд 51
Логарифмическая Линейка (созвездие) — Лаг (Лот) (лат. Lochium Funis) отменённое созвездие южного полушария
Созвездие не пользовалось популярностью среди астрономовСозвездие не пользовалось популярностью среди астрономов. Ныне созвездие не занесено Международным астрономическим союзомСозвездие не пользовалось популярностью среди астрономов. Ныне созвездие не занесено Международным астрономическим союзом в официальныйсписок созвездий.
Логарифмическая Линейка (созвездие)
Слайд 53Задание 17 № 507646. Решите неравенство
Решение.
Левая часть неравенства имеет смысл
и
то есть при
и
При этих условиях получаем:
Сделаем замену
тогда
Из полученного набора нужно ещё исключить точку 2.
Ответ:
Слайд 57Вывод:
Многие природные явления не могли быть изучены без понятия логарифма;
Логарифмы
Понятие логарифма широко применяется человеком во многих науках
Изобретение логарифмов можно смело поставить рядом с другими, более древним великим изобретением индусов – нашей десятичной системы нумерации.
Гунтер изобрел очень популярный прежде счетный прибор – логарифмическую линейку.
Логарифмическая спираль – единственный тип спирали, не меняющей своей формы при увеличении размеров. Это свойство объясняет, почему логарифмическая спираль так часто встречается в природе
Знания о логарифмах необходимы и на ЕГЭ по математике.
.
Слайд 58
Логарифмы — это все! Музыка и звуки!
И без них никак нельзя
Вот вы когда-нибудь слыхали
О логарифмической спирали?
Закручены по ней рога козлов.
И не найдете вы на них нигде узлов.
Моллюсков многих и улиток
Ракушки тоже все завиты.
И как сказал поэт великий Гете:
«Вы совершеннее строенья не найдете!»
В подсолнухе семечки тоже закручены,
И паука все плетенья заучены.
Наверняка, и о том вы не знали,
Галактики тоже кружат по спирали!
Слайд 59
ВЫВОД:
Мы постарались проследить, как в ходе истории возникала необходимость введения и
Слайд 60
С результатами работы мы выступили: перед учениками 10 класса нашей школы;
Выступили на школьной научно-исследовательской конференции в апреле 2015 года;
Научились пользоваться логарифмической линейкой.
Практическая значимость
Слайд 61 Использованная литература
1.Виленкин Н.Я. Алгебра и математический анализ. 11 кл. :Учеб.
5. Лиман М.М. Школьникам о математике и математиках. – М.: Просвещение, 1981, - 130с.
Ресурсы сети интернет:
1. Сайт Дмитрия Гущина «РЕШУ ЕГЭ»
2. Сайт http://alexlarin.net/
3.https://ru.wikipedia.org/wiki/%CB%EE%E3%E0%F0%E8%F4%EC%E8%F7%E5%F1%EA%E0%FF_%EB%E8%ED%E5%E9%EA%E0
4.http://dic.academic.ru/dic.nsf/sea/4735/
5.http://otherreferats.allbest.ru/mathematics/00215376_0.html
















































![Презентация к исследовательскому проекту по математике Логарифмы вокруг нас Решите неравенство: log2x(2x2-4x+6) ≤ log2x(x2+x).Решение. Ответ. (0; 0,5)U[2; 3]. Решите неравенство: log2x(2x2-4x+6) ≤ log2x(x2+x).Решение. Ответ. (0; 0,5)U[2; 3].](/img/thumbs/beec4b4633fffa34445fe4f6a69ec2ce-800x.jpg)