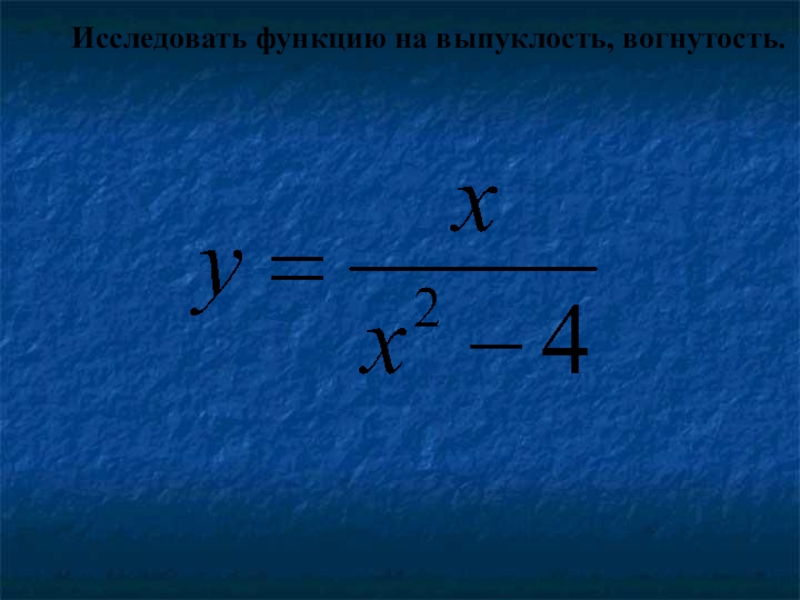- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Построение графиков с помощью производной
Содержание
- 1. Построение графиков с помощью производной
- 2. Исследование функций и построение графиков с помощью производной
- 3. «…нет ни одной области в математике, которая
- 4. Цели урока: ⮚ Образовательные. Формировать:- навыки
- 5. I этап. Актуализация ЗУН, необходимых
- 6. Необходимое условие возрастания и убывания функцииТ е
- 7. Достаточные условия возрастания и убывания функцииТеорема Лагранжа.
- 8. Достаточное условие возрастания функцииТеорема.
- 9. Достаточное условие убывания функцииТеорема.
- 10. ααФункция возрастает α < 900
- 11. Правило нахождения интервалов монотонности1) Вычисляем производную
- 12. Правило нахождения интервалов монотонности2) Критическими точками область
- 13. Правило нахождения интервалов монотонности 3) Определим
- 14. Исследование экстремумов функции Необходимое условие экстремума.
- 15. Теорема Ферма лишь необходимое условие
- 16. Достаточные условия существования экстремума в точкеПризнак максимума
- 17. Достаточные условия существования экстремума в точкеПризнак минимума
- 18. Достаточные условия выпуклости вверх и вниз графика
- 19. α1α2График выпуклый α - убывает
- 20. Точки перегибаНайти критические точки функции по второй
- 21. Заполните таблицуЗадание для всех учащихся.II этап. Обобщение и систематизация знаний и способов деятельности
- 22. Слайд 22
- 23. №2 По графику производной некоторой функции укажите
- 24. 3. На рисунке изображён график производной функции
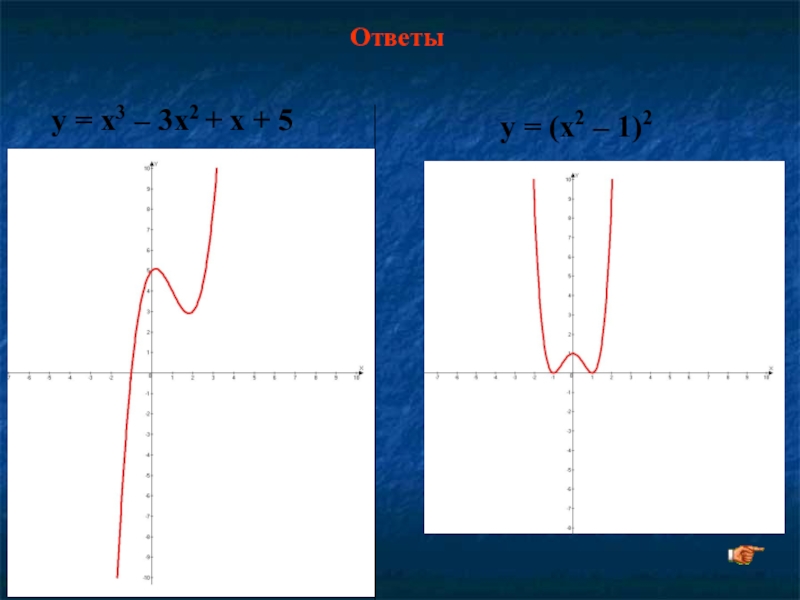
- 25. у = x3 – 3x2 + x + 5 у = (x2 – 1)2Ответы
- 26. III этап. Усвоение образца комплексного применения ЗУН.Практическая
- 27. Работа на компьютереРабота на местах
- 28. Работа с ЭУП «Математика – практикум 5-11»
- 29. Слайд 29
- 30. Работа на компьютереРабота на местах
- 31. Работа на компьютереРабота на местах
- 32. Работа в группах
- 33. Исследовать функцию на выпуклость, вогнутость.
- 34. Мини - исследовательская работа Выбери задание1. 3. 5. 2. 4. 6.
- 35. Д о м а ш н е
Слайд 1 Урок на тему : «Исследование функции с помощью производной» с использованием
Слайд 3«…нет ни одной области в математике, которая когда-либо не окажется применимой
Н.И. Лобачевский
Скажи мне, и я забуду.
Покажи мне, и я запомню.
Дай мне действовать самому,
И я научусь.
Конфуций
Слайд 4Цели урока:
⮚ Образовательные.
Формировать:
- навыки прикладного использования аппарата производной;
- выявить уровень овладения учащимися комплексом знаний и умений по исследованию функции и ликвидировать пробелы в знаниях в соответствии с требованиями к математической подготовке учащихся.
⮚ Развивающие.
Развивать:
- способности к самостоятельному планированию и организации работы
- навыки коррекции собственной деятельности через применение информационных технологий;
- умение обобщать, абстрагировать и конкретизировать знания при исследовании функции.
⮚ Воспитательные.
Воспитывать:
- познавательный интерес к математике;
- информационную культуру и культуру общения;
- самостоятельность, способность к коллективной работе.
Слайд 5 I этап. Актуализация ЗУН, необходимых для творческого применения знаний
Необходимое условие возрастания и убывания функции
Достаточное условие возрастания и убывания функции
Необходимое условие экстремума. (теорема Ферма)
Признак максимума функции.
Признак минимума функции.
Достаточные условия выпуклости вверх и вниз графика функции
Слайд 6Необходимое условие возрастания и убывания функции
Т е о р е м
Слайд 7Достаточные условия возрастания и убывания функции
Теорема Лагранжа.
Если функция f(x), х∈[а;b],
f(a) – f(b) = f `(c)(b – a)
Слайд 8Достаточное условие возрастания функции
Теорема.
Слайд 9Достаточное условие убывания функции
Теорема.
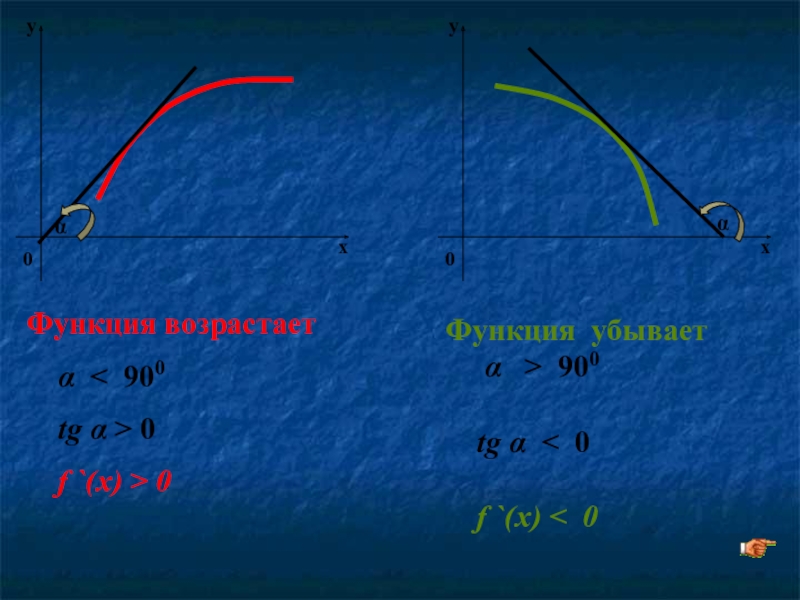
Слайд 10
α
α
Функция возрастает
α < 900
tg α > 0
Функция убывает
α > 900
tg α < 0
f `(x) < 0
Слайд 11Правило нахождения интервалов монотонности
1) Вычисляем производную f `(x) данной функции
Слайд 12Правило нахождения интервалов монотонности
2) Критическими точками область определения функции f(x) разбивается
Слайд 13Правило нахождения интервалов монотонности
3) Определим знак f `(x) на
Слайд 14Исследование экстремумов функции
Необходимое условие экстремума.
(теорема Ферма)
Если точка
f `(x) = 0.
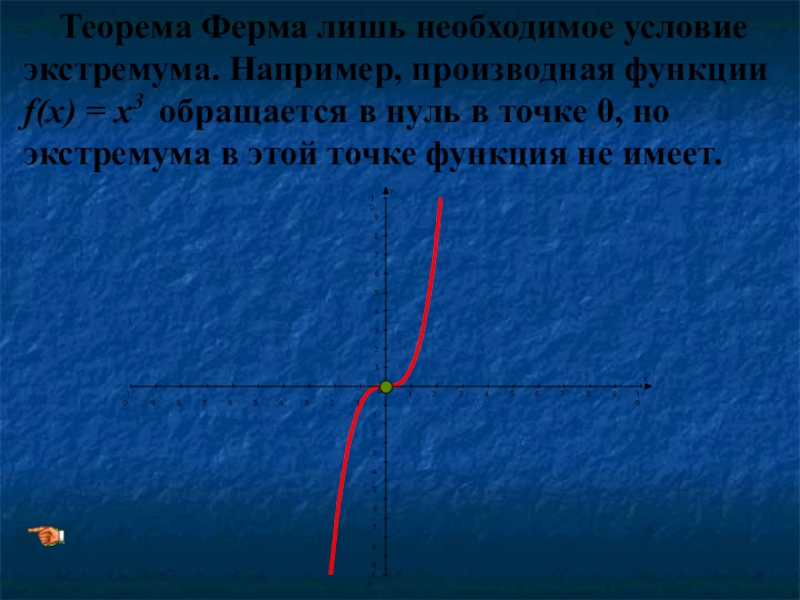
Слайд 15 Теорема Ферма лишь необходимое условие экстремума. Например, производная функции
0
Слайд 16Достаточные условия существования экстремума в точке
Признак максимума функции. Если функция f
построение
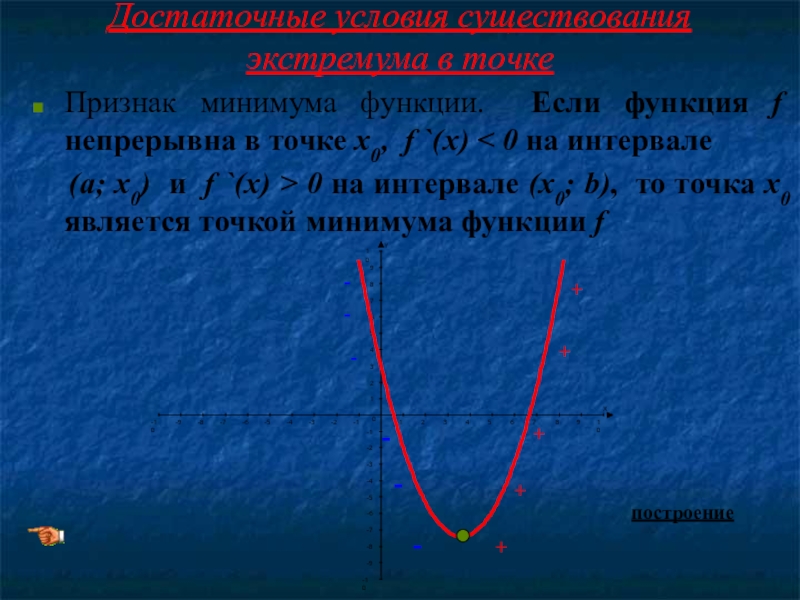
Слайд 17Достаточные условия существования экстремума в точке
Признак минимума функции. Если функция f
(а; х0) и f `(x) > 0 на интервале (х0; b), то точка х0 является точкой минимума функции f
X
Y
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
10
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
10
0
построение
Слайд 18Достаточные условия выпуклости вверх и вниз графика функции
Т е о р
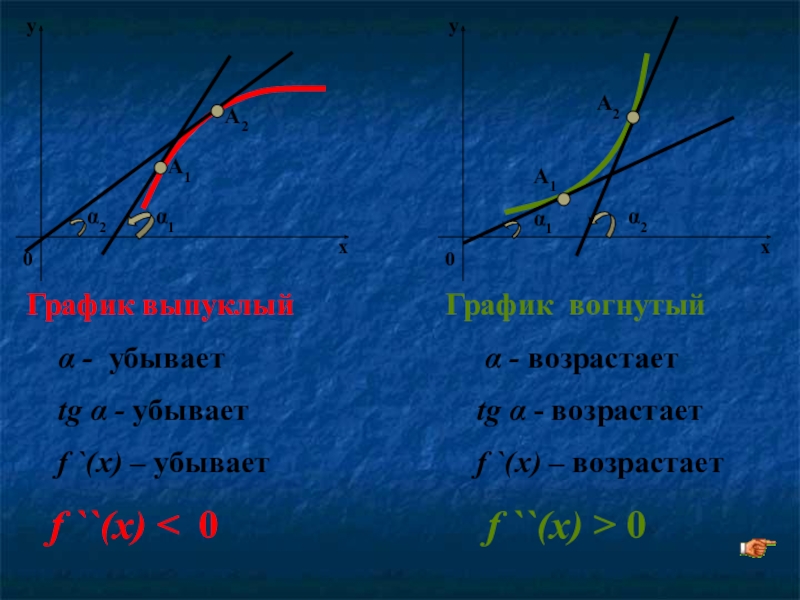
Слайд 19
α1
α2
График выпуклый
α - убывает
tg α - убывает
f ``(x) < 0
График вогнутый
α - возрастает
tg α - возрастает
f `(x) – возрастает
f ``(x) > 0
α1
α2
A1
A2
A1
A2
Слайд 20Точки перегиба
Найти критические точки функции по второй производной.
Исследовать знак второй производной
Если f ``(х) меняет свой знак при переходе аргумента через критическую точку х0, то (х0; f(х0)) - точка перегиба графика данной функции
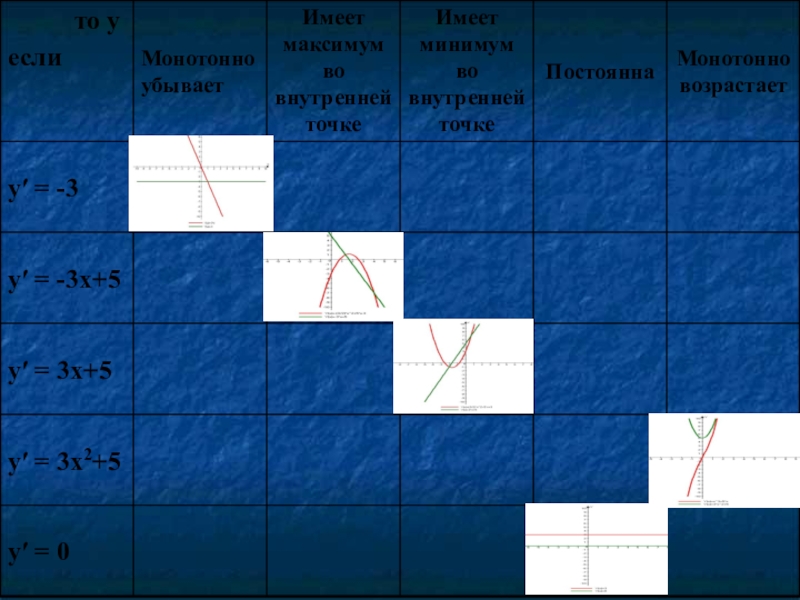
Слайд 21Заполните таблицу
Задание для всех учащихся.
II этап. Обобщение и систематизация знаний и
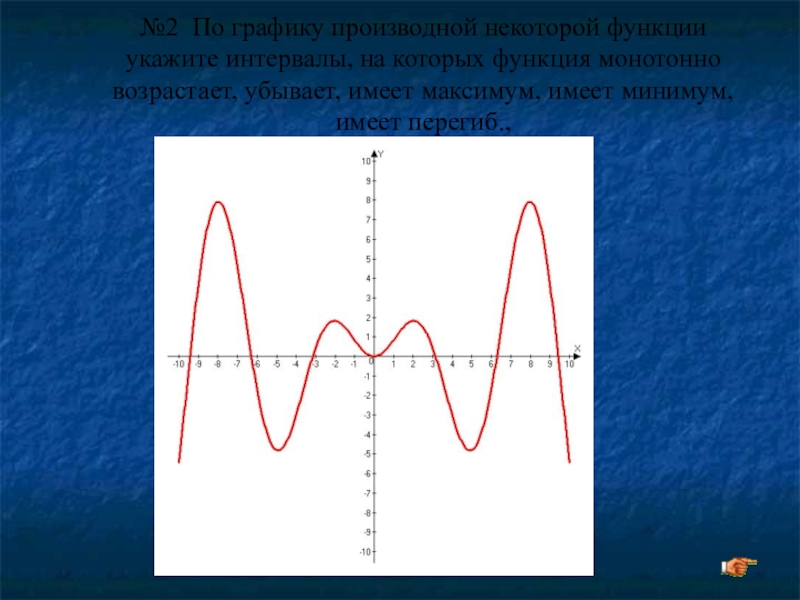
Слайд 23№2 По графику производной некоторой функции укажите интервалы, на которых функция
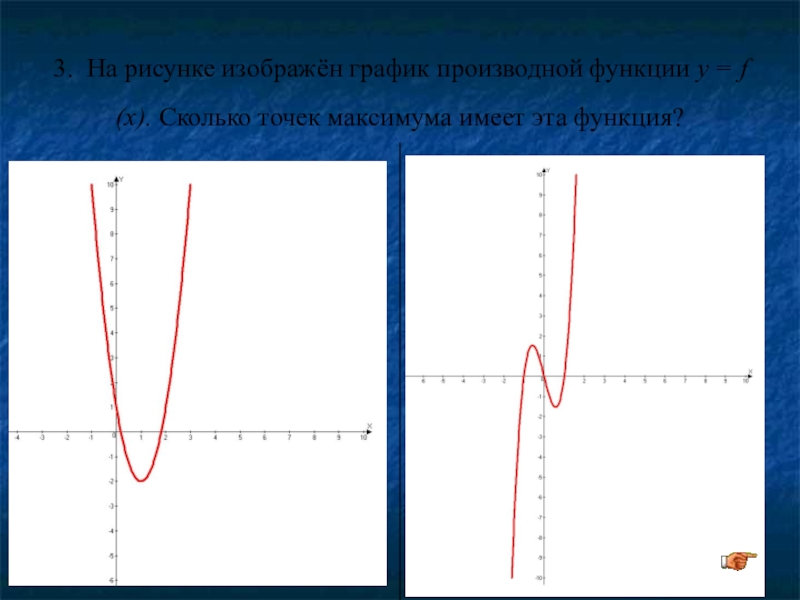
Слайд 243. На рисунке изображён график производной функции y = f (x).
Слайд 26III этап. Усвоение образца комплексного применения ЗУН.
Практическая работа с применением электронного
Слайд 35Д о м а ш н е е з
1. № 45, 41 (устно), 39 (31)
2. Определите, при каком значении параметра b максимум функции равен 3?
Подведение итогов урока.





![Построение графиков с помощью производной Достаточные условия возрастания и убывания функцииТеорема Лагранжа. Если функция f(x), х∈[а;b], Достаточные условия возрастания и убывания функцииТеорема Лагранжа. Если функция f(x), х∈[а;b], непрерывна на отрезке [а;b] и дифференцируема](/img/thumbs/c23fc5338f68eb14383c9fd354b8ca22-800x.jpg)