- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Первообразная( 11 класс )
Содержание
- 1. Первообразная( 11 класс )
- 2. Содержание Понятие первообразнойТаблица первообразных Три правила нахождения первообразных
- 3. Понятие первообразнойФункцию F(x) называют первообразной для функции
- 4. Примерыf(x) = 2x; F(x) = x2
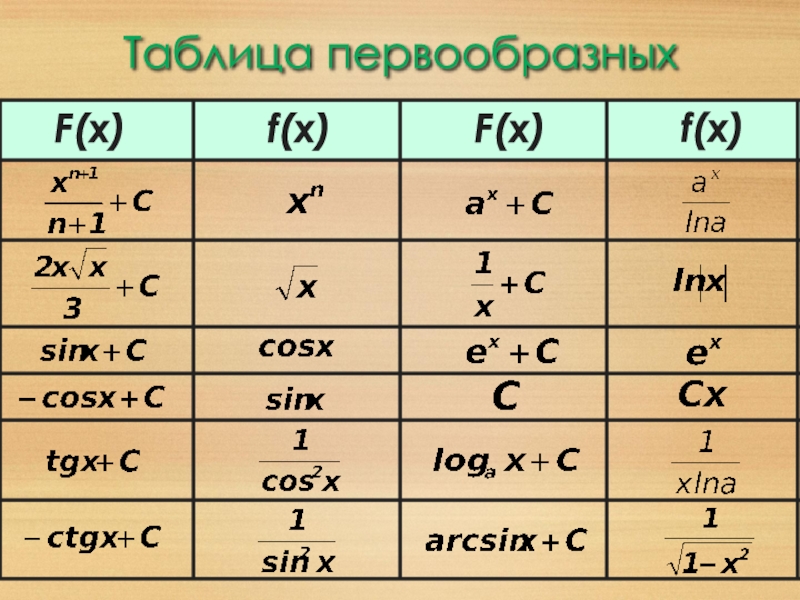
- 5. Таблица первообразныхf(x)F(x)F(x)
- 6. Три правила нахождения первообразных1º Если F(x) есть
- 7. Неопределенный интегралНеопределенным интегралом от непрерывной на интервале
- 8. Примеры
Содержание Понятие первообразнойТаблица первообразных Три правила нахождения первообразных
Слайд 3Понятие первообразной
Функцию F(x) называют первообразной для функции f(x) на интервале (a;
b), если на нем производная функции F(x) равна f(x):
Операцию, обратную дифференцированию называют интегрированием.
Слайд 4Примеры
f(x) = 2x; F(x) = x2
F′(x)=
(x2)′ = 2x = f(x)
f(x) = – sin x; F(x) = сos x
F′(x)= (cos x)′ = – sin x = f(x)
f(x) = 6x2 + 4; F(x) = 2x3 + 4x
F′(x)= (2x3 + 4x)′ = 6x2 + 4 = f(x)
f(x) = 1/cos2 x; F(x) = tg x
F′(x)= (tg x)′ = 1/cos2 x= f(x)
Слайд 6Три правила нахождения первообразных
1º Если F(x) есть первообразная для f(x), а
G(x) –
первообразная для g(x), то F(x) + G(x) есть
первообразная для f(x) + g(x).
первообразная для g(x), то F(x) + G(x) есть
первообразная для f(x) + g(x).
2º Если F(x) есть первообразная для f(x), а k –
постоянная, то функция kF(x) есть первообразная
для kf(х).
Слайд 7Неопределенный интеграл
Неопределенным интегралом от непрерывной на интервале (a; b) функции f(x)
называют любую ее первообразную функцию.
Где С – произвольная постоянная (const).
