- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Открытый урок по алгебре в 9 классе
Содержание
- 1. Открытый урок по алгебре в 9 классе
- 2. ЗАДАНИЕ НА ДОМ
- 3. Цели урока: Образовательная – рассмотреть основные свойства
- 4. Слайд 4
- 5. Слайд 5
- 6. Слайд 6
- 7. ОПРЕДЕЛЕНИЕ 1
- 8. ОПРЕДЕЛЕНИЕ 2 Функцию у = f(x)
- 9. Монотонность функцииx0yx0yх1х2f(х1)f(х2)f(x) - возрастающаяf(x) – убывающаях1f(х1)х2f(х2)y = f(x)y = f(x)
- 10. Найти промежуткивозрастания и убывания функцийx0yy = f(x)3-1-33-244
- 11. ОПРЕДЕЛЕНИЕ № 3 Функция называется ограниченной
- 12. ОПРЕДЕЛЕНИЕ 4 Функция называется ограниченной сверху
- 13. Ограниченность функцииx0yy = f(x)my = f(x) –
- 14. ОПРЕДЕЛЕНИЕ 5 Число m называется наименьшим
- 15. ОПРЕДЕЛЕНИЕ 6 Число m называется наибольшим
- 16. Наименьшее значение функцииx0yy = f(x)xx0m= f(x0)f(x)
- 17. Наибольшее значение функцииx0yy = f(x)xx0M= f(x0)f(x)
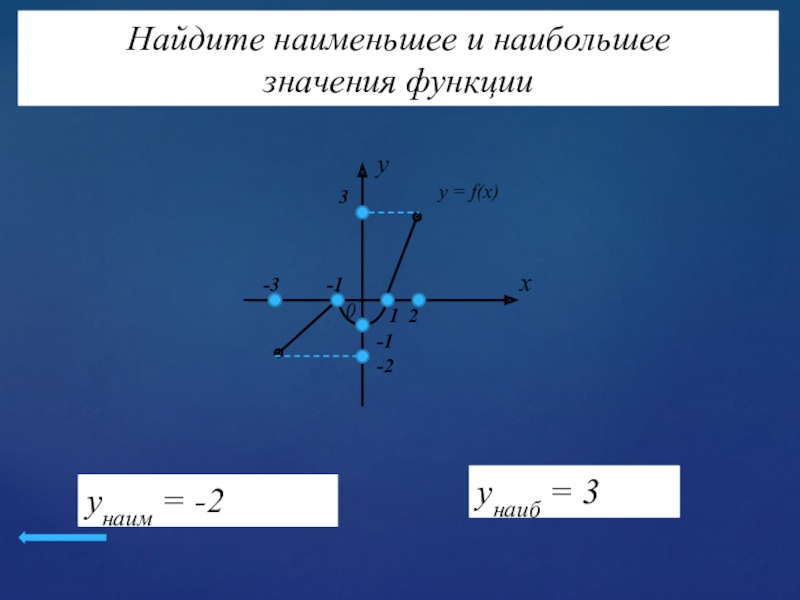
- 18. Найдите наименьшее и наибольшее значения функцииx0yy = f(x)12-1-1-33-2yнаим = -2 yнаиб = 3
- 19. Определите выпуклость функцииx0yy = f(x)y = f(x)
- 20. СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ 1. Область определения функции D(f).2.
- 21. Линейная функция функция вида y = k
- 22. Квадратичная функция функция вида y = kx²,
- 23. Обратная пропорциональность функция вида y =
- 24. функция вида y = ;
- 25. функция вида y = |x|; 1. D(
- 26. ПРИМЕР № 1. Исследовать на монотонность функцию у = х -3РешениеОбозначим f(x)=x-3, пусть x1
- 27. Каждый график соотнесите с соответствующей ему формулой:
ЗАДАНИЕ НА ДОМ
Слайд 3Цели урока:
Образовательная – рассмотреть основные свойства числовых функций и иллюстрируя
их графически; дать им более точные определения.
Развивающая – развитие логического мышления, анализа, памяти.
Воспитательная – воспитание уверенности, внимания.
Оборудование: компьютер, проектор, презентация.
Актуальность:
задания по данной теме встречаются в ГИА по математике в 9 классе и в ЕГЭ - 11 класса;
чтение графиков функций имеет большое практическое значение.
Развивающая – развитие логического мышления, анализа, памяти.
Воспитательная – воспитание уверенности, внимания.
Оборудование: компьютер, проектор, презентация.
Актуальность:
задания по данной теме встречаются в ГИА по математике в 9 классе и в ЕГЭ - 11 класса;
чтение графиков функций имеет большое практическое значение.
Слайд 7ОПРЕДЕЛЕНИЕ 1
Функцию у = f(x)
называют возрастающей на множестве X Є D(f), если для любых двух элементов x1 и х2 множества Х, таких, что x1 < x2 , выполняется неравенство
f(x1) < f(x2).
f(x1) < f(x2).
Слайд 8ОПРЕДЕЛЕНИЕ 2
Функцию у = f(x) называют убывающей на множестве
X Є D(f), если для любых двух элементов x1 и х2 множества Х, таких, что x1 < x2 , выполняется неравенство
f(x1) > f(x2).
f(x1) > f(x2).
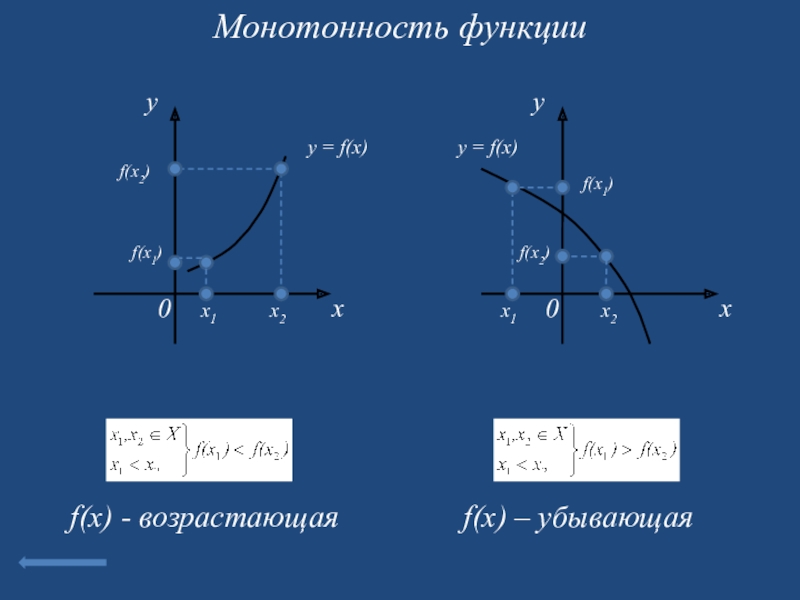
Слайд 9Монотонность функции
x
0
y
x
0
y
х1
х2
f(х1)
f(х2)
f(x) - возрастающая
f(x) – убывающая
х1
f(х1)
х2
f(х2)
y = f(x)
y = f(x)
Слайд 10Найти промежутки
возрастания и убывания функций
x
0
y
y = f(x)
3
-1
-3
3
-2
4
4
y = f(x) –
возрастает на [-3;-1]
x
0
y
y = f(x)
3
-1
-3
3
-2
4
4
5
y = f(x) – убывает на [-1;4]
Слайд 11ОПРЕДЕЛЕНИЕ № 3
Функция называется ограниченной снизу на множестве X
Є D(f), если существует такое число m, что для любого значения х Є D(f) выполняется неравенство
f(x) > m.
f(x) > m.
Слайд 12ОПРЕДЕЛЕНИЕ 4
Функция называется ограниченной сверху на множестве X Є
D(f), если существует такое число М, что для любого значения
х Є D(f) выполняется неравенство
f(x) < М.
х Є D(f) выполняется неравенство
f(x) < М.
Слайд 13Ограниченность функции
x
0
y
y = f(x)
m
y = f(x) – ограниченна снизу
у =
m
f(x) > m
x
0
y = f(x)
M
y = f(x) – ограниченна сверху
y = M
f(x) < М
y
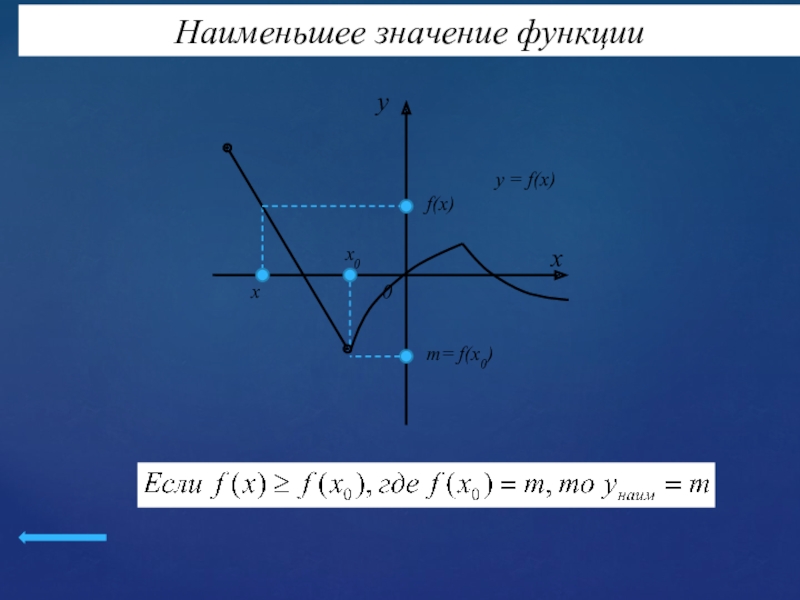
Слайд 14ОПРЕДЕЛЕНИЕ 5
Число m называется наименьшим значением функции у =
f(x) на множестве X Є D(f), если:
Существует число x0 Є D(f) такое, что f(x0) = M;
Для любого значения х Є Х выполняется неравенство
f(x) ≥ f(x0).
Существует число x0 Є D(f) такое, что f(x0) = M;
Для любого значения х Є Х выполняется неравенство
f(x) ≥ f(x0).
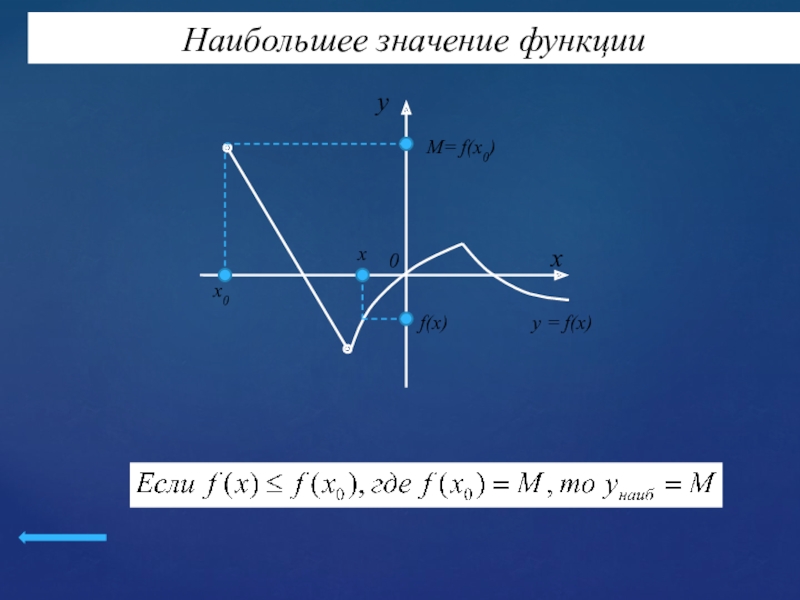
Слайд 15ОПРЕДЕЛЕНИЕ 6
Число m называется наибольшим значением функции у =
f(x) на множестве X Є D(f), если:
Существует число x0 Є D(f) такое, что f(x0) = M;
Для любого значения х Є Х выполняется неравенство
f(x) ≤ f(x0).
Существует число x0 Є D(f) такое, что f(x0) = M;
Для любого значения х Є Х выполняется неравенство
f(x) ≤ f(x0).
Слайд 19Определите выпуклость функции
x
0
y
y = f(x)
y = f(x) – выпукла вниз на
(-∞; 0]
y = f(x) – выпукла вверх на [0; +∞)
Слайд 20СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
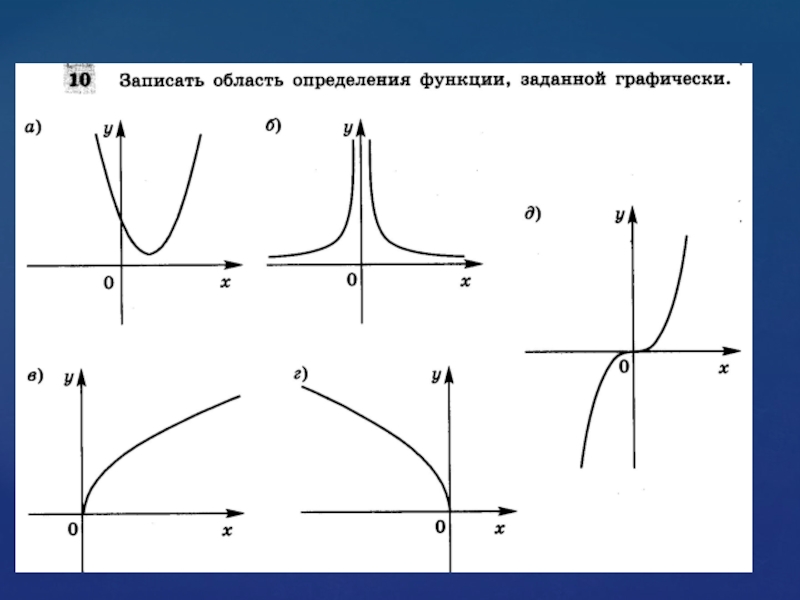
1. Область определения функции D(f).
2. Промежутки возрастания и убывания
(монотонность) функции.
3. Ограниченность функции.
4. Наибольшее и наименьшее значения функции.
5. Непрерывность функции.
6. Область значений функции Е(f).
7. Выпуклость функции.
3. Ограниченность функции.
4. Наибольшее и наименьшее значения функции.
5. Непрерывность функции.
6. Область значений функции Е(f).
7. Выпуклость функции.
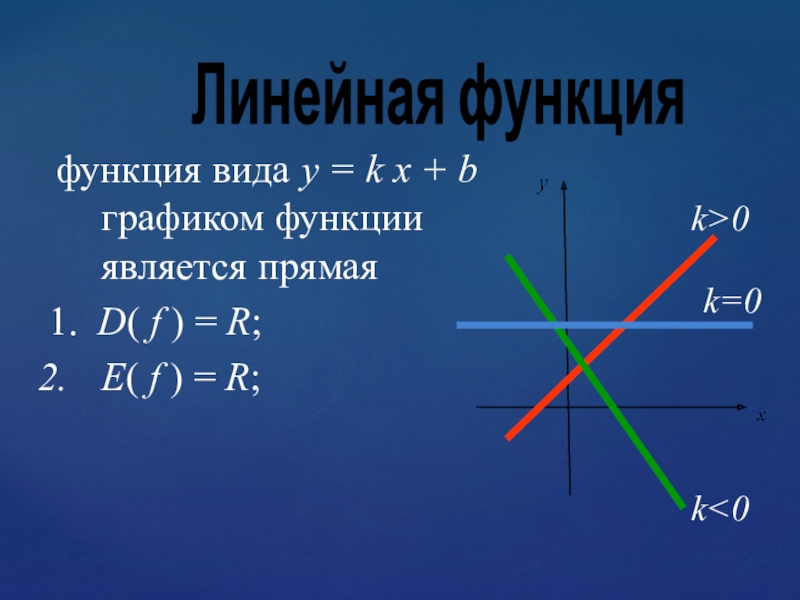
Слайд 21Линейная функция
функция вида y = k х + b графиком
функции является прямая
1. D( f ) = R;
E( f ) = R;
1. D( f ) = R;
E( f ) = R;
k>0
k<0
k=0
Слайд 22Квадратичная функция
функция вида y = kx², k>0; графиком функции является
парабола, ветви которой направлены вверх
D( f ) = R;
2. E( f ) = [0;∞);
D( f ) = R;
2. E( f ) = [0;∞);
Слайд 23Обратная пропорциональность
функция вида y = ; графиком функции
является гипербола
1. D( f ) = (-∞;0) (0;∞)
2. E( f ) = (-∞;0) (0;∞);
1. D( f ) = (-∞;0) (0;∞)
2. E( f ) = (-∞;0) (0;∞);
k
x
k>0
k<0
Слайд 24функция вида y = ; графиком функции является ветвь
параболы.
1. D( f ) = [0;∞);
2. E( f ) = [0;∞);
1. D( f ) = [0;∞);
2. E( f ) = [0;∞);
Функция корня
Слайд 25функция вида y = |x|;
1. D( f ) = R;
2. E( f ) = [0;∞);
3. график функции на промежутке [0;∞) совпадает с графиком функции у = х, а на промежутке (-∞;0] – с графиком функции у = -х
Функция модуля
Слайд 26ПРИМЕР № 1.
Исследовать на монотонность функцию у = х -3
Решение
Обозначим
f(x)=x-3, пусть x1 2x1-3<2x2-3,
f(x1)< f(x1), значит заданная функция убывает (на всей числовой прямой).
f(x1)< f(x1), значит заданная функция убывает (на всей числовой прямой).





![Открытый урок по алгебре в 9 классе Найти промежуткивозрастания и убывания функцийx0yy = f(x)3-1-33-244 y = f(x) – Найти промежуткивозрастания и убывания функцийx0yy = f(x)3-1-33-244 y = f(x) – возрастает на [-3;-1]x0yy = f(x)3-1-33-2445 y](/img/thumbs/bfa108e4e217d0078e06ab2d0eaeb487-800x.jpg)





![Открытый урок по алгебре в 9 классе Определите выпуклость функцииx0yy = f(x)y = f(x) – выпукла вниз на Определите выпуклость функцииx0yy = f(x)y = f(x) – выпукла вниз на (-∞; 0]y = f(x) – выпукла](/img/thumbs/5d4d69e8b95a82006375b4398c3e95e0-800x.jpg)