Презентация, доклад на тему Электронная рабочая тетрадь. Алгебра. 7 класс

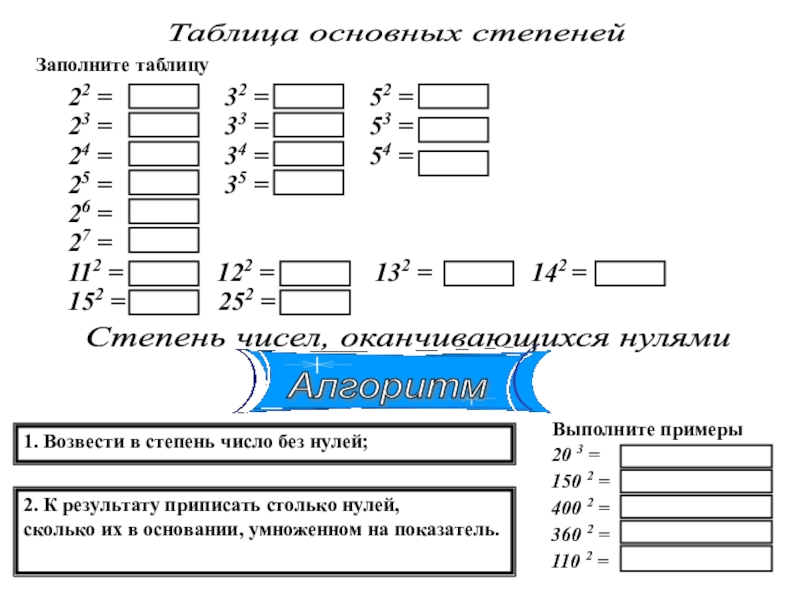
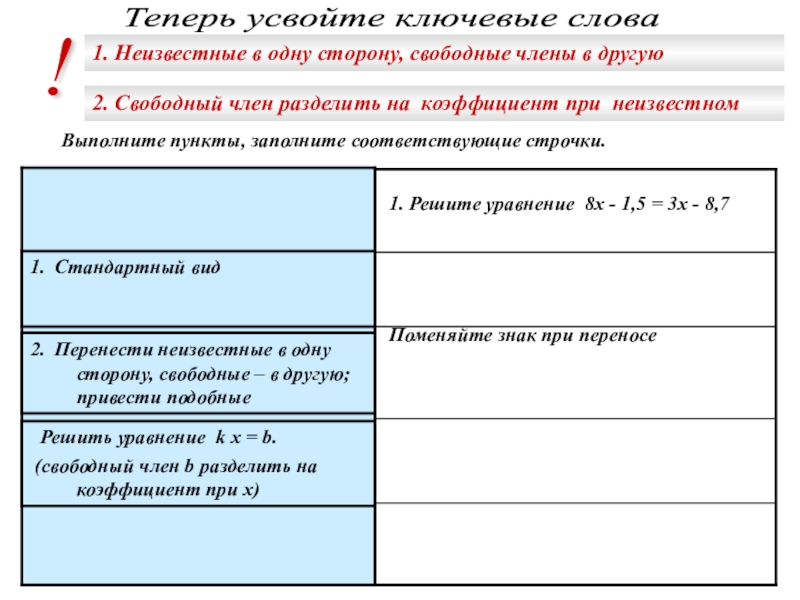
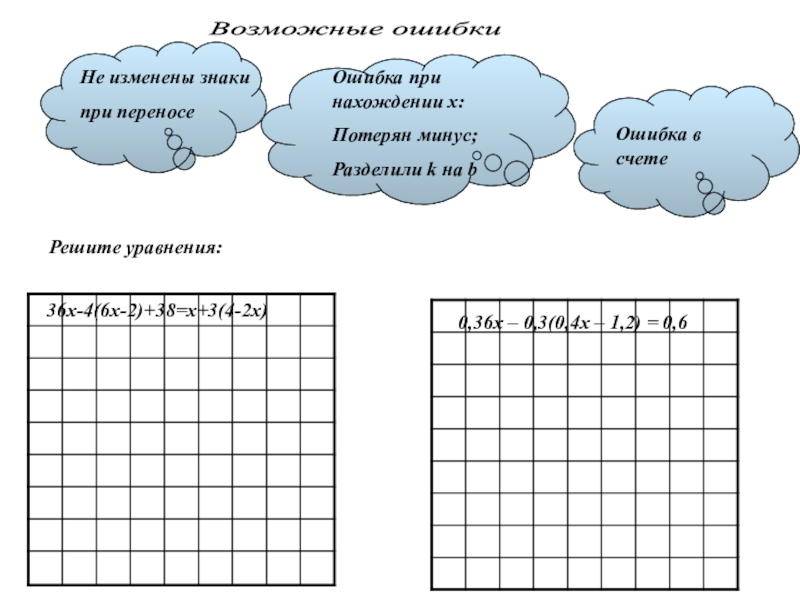
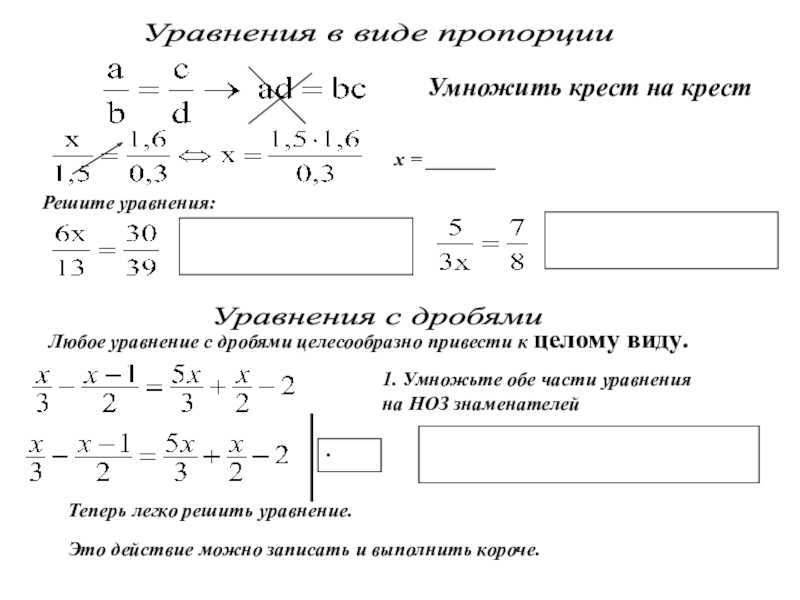
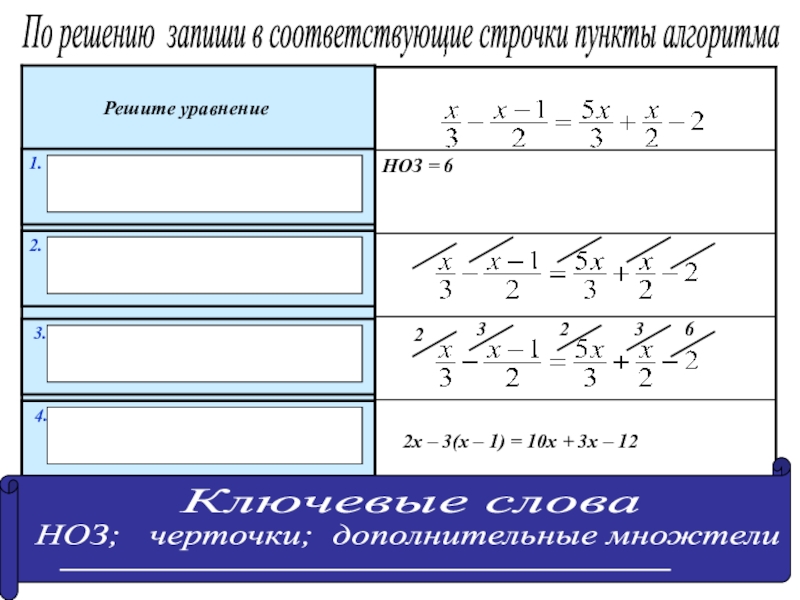
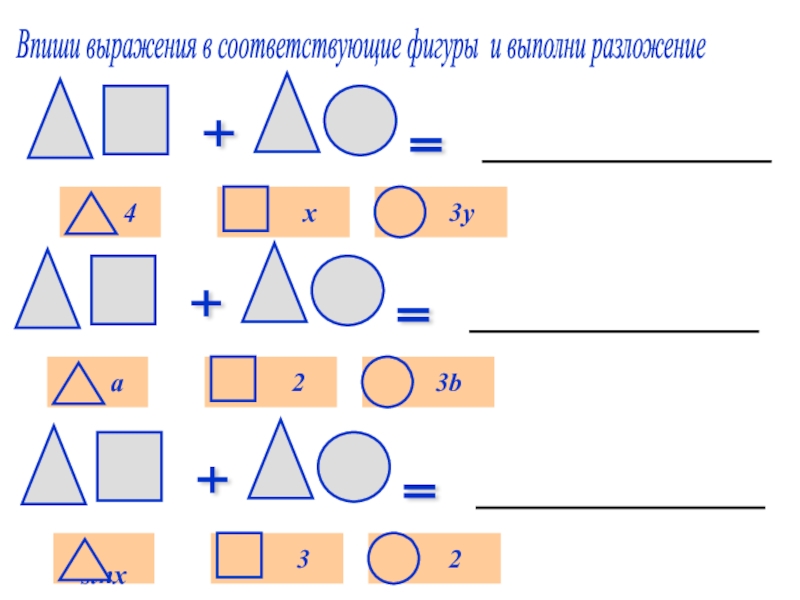
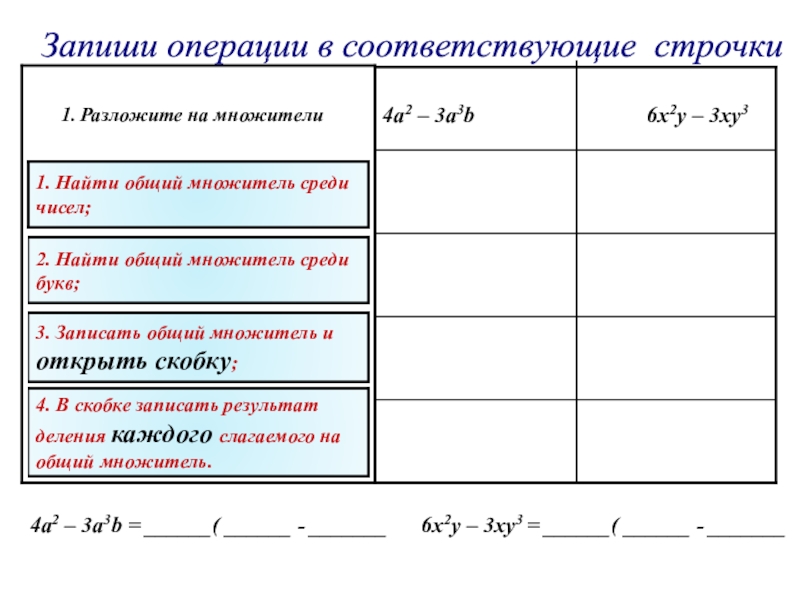
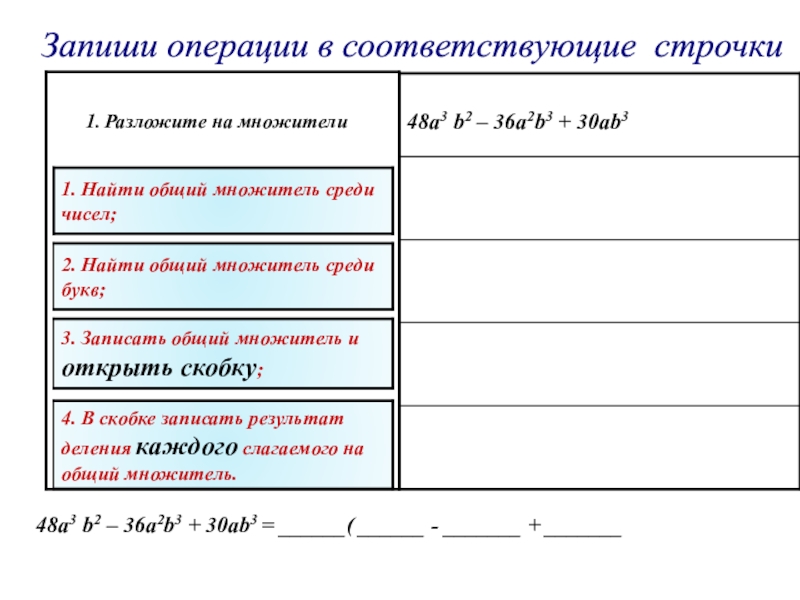
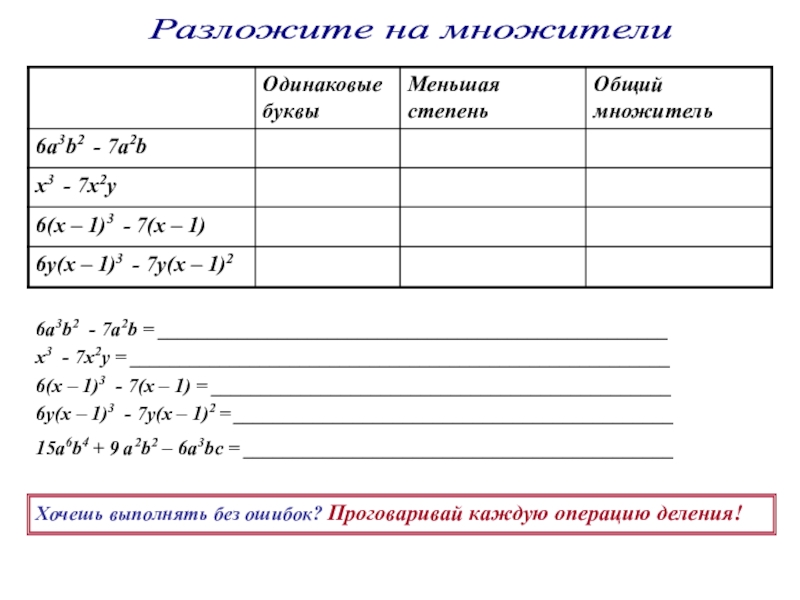
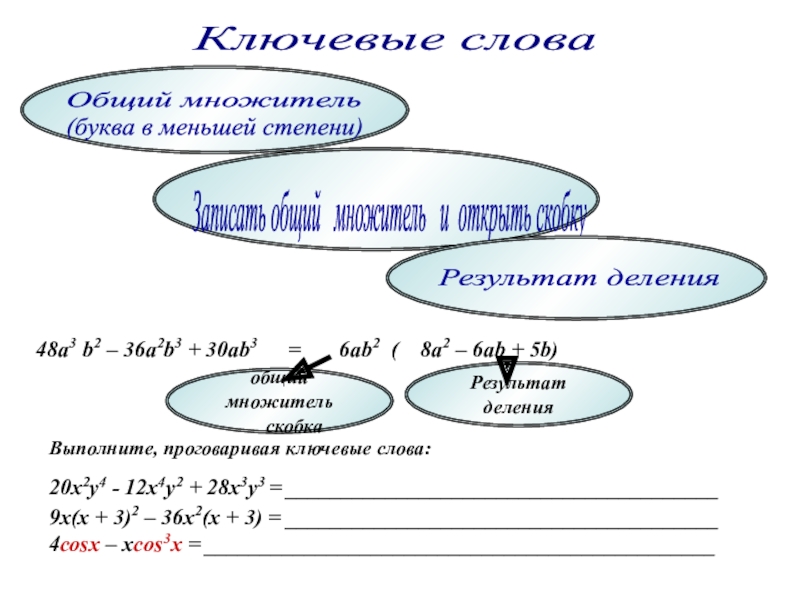
а – называется _________________
n – называется __________________
an – называется __________________

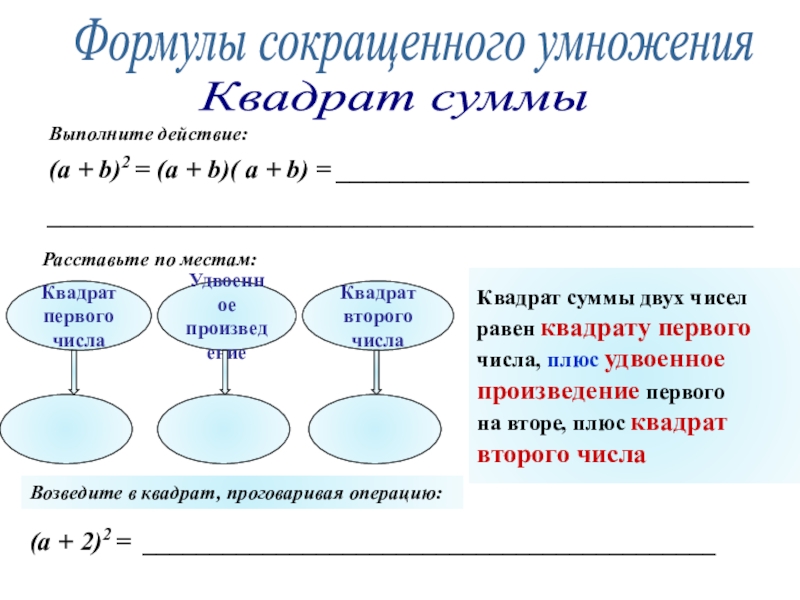
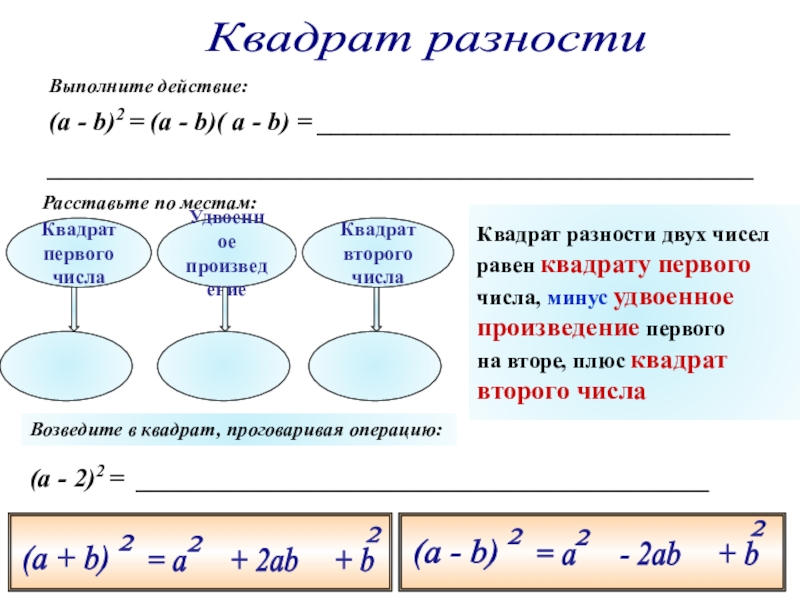
Если n = 2, например, х2, 52, (a + b)2, то говорят икс в квадрате, пять в квадрате, а плюс b в квадрате.
Если n = 3, например, х3, 53, (a + b)3, то говорят икс в кубе, пять в кубе, а плюс b в кубе.
При других показателях, например, х5, 56, (a + b)4, говорят икс в пятой степени, пять в шестой степени, а плюс b в четвертой степени.

степенью с натуральным показателем

аn

основанием

показателем

степенью

а1 = _____

Единицу в показателе не пишут.

1n = _____

Нуль в любой степени равен _____________________.

0n = _____

1. В таблицу проставьте номера выражений в четной и нечетной степени:

22;
(-2)3;
0,33;
(½ )6;
(-10)5;
a8;
(4b)3;
(x-y)4;

9) 2,62;
10) (-a)10;
11) (1 ½ )9;
12) (ab )6;
13) (3)2n;
14) a2n +1;
15) (4b) 2k +2;
16) (a +b)4n – 1 ;

1. Возвести в степень число без нулей;

1. Возвести в степень число, не взирая на запятую;

Знак степени

Определите знак степени, используя определение степени:

(-2)2 = (-2) (-2) = +
(-2)3=_________________________
(-2)4=_________________________
(-2)5=_________________________
(-2)6=_________________________

Сделайте вывод!
Минус в четной степени будет
__________________________
Минус в нечетной степени будет
__________________________

Выполните примеры. Сначала поставьте знак, потом вычисляйте.
(-2)4 = ______________________
- (2х)4 = _______________________
( - 2/5)3 = _______________________
- (-а)5 = _______________________

33∙ 32 = _________________________________________
(0,2)2 ∙ (0,2) = ____________________________________
a3 ∙ a3 = _________________________________________
a n ∙ a m =________________________________________

Чтобы перемножить степени с одинаковыми основаниями, надо: основание ___________________________,a показатели _______________________.

Сделайте вывод. Заполните пропуски

основание оставить тем же

сложить

сложить

Сделайте вывод. Заполните пропуски

основание оставить тем же

вычесть

вычесть

5) k3·k7· k4 = k

6) 103·10т = 10

7) 103+2m·10т = 10

Представьте в виде степени. Найдите значение выражения:

1) 23·24 = _______

2) 33·3 = _______

3) 103·102 = _______

4) 0,53·0,5 = _______

5) 16·24 = _______

6) 33·9 = _______

7) 2·103· 3·102 = __________

8) 32·32 = _________

Представьте частное в виде степени:

6) 103:10т = 10

Представьте в виде степени. Найдите значение выражения:

1) 25:24 = _______

= _______

3) 109/106 = _______

4) 0,53:0,5 = _______

5) 32/24 = _______

6) 34/27 = _______

= __________

8) x 6 : x = _________

Любое число кроме ___________ равно _____

10

14

5

8

14

3+т

3+3т

12

28 =256

81

100000

0,0625

35 =243

600000

210=1024

3

2

2

1+т

3

3-т

128

2

64

1000

2

3

2/3·104

х5

1

нуля

1

2

0,0625

(22) 3 = (2· 2)· (2· 2) · (2· 2) =

{

{

2

3

(33)2 = _________________________________________
(0,22)4 = ________________________________________
(a3 )5 = _________________________________________
(a n) m =________________________________________

Чтобы возвести степень в степень, надо: основание ________________________,a показатели _______________________.

Сделайте вывод. Заполните пропуски

основание оставить тем же

умножить

умножить

6) (103 )т = 10

7) (103+2m )т = 10

Представьте в виде степени. Найдите значение выражения:

1) (-23)4 = _______

2) (-32)2 = _______

3) ((-10)2 )3 = _______

4) (0,54 )2 = _______

Свойства степеней

Одинаковые основания

Показатели ________________

Показатели ________________

Показатели ________________

умножение

сложить

дробь

вычесть

Возведение в степень

умножить

Представьте составное числа в виде произведения степеней с простыми основаниями:

1) 12 = _________

2) 24 = _________

3) 75 = __________

4) 48 = ____________

5) 72 = _________

6) 250 = _________

7) 54 = __________

8) 80 = ____________

Разложите числа на простые множители:

576

540

1296

864

864 =

576 =

540 =

1296 =

22·3

23·3

52·3

24·3

23·32

53·2

33·2

24·5

2

432

2

216

2

108

2

54

2

27

33

25·33

26·32

22·33·5

24·34

Представьте в виде произведения степеней с простым основанием:

1) (12)2 = _________

2) 64 = _________

3) (15)3 = __________

4) (48)3 = ____________

5) 722 = _________

6) 84 = _________

7) 27 2= __________

8) (80 )3 = ___________

при с = -3 ответ: _____

при с = ¼ ответ: ________

(2 · 3)3 = 2· 2 · 2 · 3 · 3· 3 = 2 3 · 33 = 108

{

3

(3 · 4)2 = _________________________________________
(0,2 · 5)4 = ________________________________________
(a ·b )5 = _________________________________________
(a b) m =________________________________________

Чтобы возвести произведение в степень, надо возвести в эту степень _________________________________________________________________.

Сделайте вывод. Заполните пропуски

{

3

32·42 = 9 · 16 = 144

1

а5 · b5

аm · bm

каждый множитель

каждый множитель

Возведите в степень:

1) (3a ) 2 = ________

2) (-2x)4 = ________

3) (ab)3 = ________

4) (-3x 2)3 = ___________

5) (xy4) 2 = ________

6) (-0,5n2) 4 = _______

7) (2 ¼ c) 2 = ________

8) (-2mn2 )3 = _________

Не забывайте!

возводить в степень коэффициент перед буквенной частью с учетом знака.

(-1,1n3 m) 2 = (-1,1)2 n6 m2 = 1,21 n6 m2

Заполните таблицу, используя свойство

Что это?

Как это?

9

16х4

а3b3

-27х6

х2y8

0,0625n8

81/16c2

-8m3 n6

Произведение степеней с разными основаниями

63 = 216

6n

(ab)3

(ab)n

а2

3

Чтобы возвести дробь в степень, можно возвести в эту степень _________________________________________________________________.

Сделайте вывод. Заполните пропуски

числитель и знаменатель

числитель и знаменатель

Возведите
в степень:

Что это?

Как это?

Заполните таблицу, используя свойство

неправильную

возвести в степень числитель и знаменатель

Деление степеней с разными основаниями

Разные основания

Что это?

Как это?

(ab) n =

a n ∙ b n =

a n + m

a n - m

a n m

сложить

вычесть

умножить

каждый
множитель

основания

числитель и
знаменатель

b
возвести в степень

a n ∙ b n

(ab) n

(-2)4, -а3, (-3х)4, - 24, (- а)3, - (х+2)2

Выполните :
(-2)4 _=____________ - (2х)4 =_____________ ( - 2/5)3 =______________
- (-а)5 =____________ (- (х -1)2)3 = __________ - 1/3 (- 3b2)3 = __________

Определите на какую цифру оканчивается 22011

Сравните:

Скорость света равна 3·108 м/с, расстояние от Земли до Солнца 1,5·1011 м. За какое время пройдет луч света от Солнца до земли?

Знаки в выражениях

Одночлены могут иметь числовой множитель и буквенную часть.

2 a2

Числовой множ.

Буквенная часть

Числовой множитель называется коэффициентом.

Коэффициенты 1 и – 1 не записываются.

Определите коэффициенты одночленов:

В стандартном виде коэффициент записывается перед буквенной частью, буквенная часть записываются латинскими прописными буквами по алфавиту.

Знак умножения ( · ) не ставится

Выполните примеры

0,2а 3(3b) =
(-2)2(4n2) =
(-1/3 c)(-9c2) =
(-2bc)2( b2c)=

3. Умножить коэффициенты ;

4. Умножить буквенную часть.

Помните!

При умножении степеней с одинаковыми основаниями показатели _______________

Выполните действия:

( - 2а)2 ( - 3ab) =
2) ( - 3a2bc)( - 5ab2c)( - 0,4abc2) =

Приведение подобных слагаемых

Одночлены, имеющие одинаковую буквенную часть называются _______________________________

Чтобы сложить подобные слагаемые, надо: ________________________________
_________________________________________________________________________

Пример:

4 а2 + 8 а – 12 а2 +5 а – 3 = (4 – 12)а2 + ( 8 + 5 )а – 3 = - 8а2 +13а – 3

4 а2 + 8 а – 12 а2 + 5 а – 3 = - 8а2 +13а – 3

2. Повторить с другими слагаемыми. Использовать двойную черту и т. д.

1. Подчеркнуть одной чертой первое слагаемое, подчеркнуть подобные, посчитать, записать;

2ху2 – 3х2у + 4 ху2 + 6х2у -8 =

2ху2 – 3х2у + 4 ху2 + 6х2у -8

Усвоим алгоритм действия

2ху2 – 3х2у + 4 ху2 + 6х2у -8 = 6ху2

6ab – 2a2b – 8ba + 4a2b + 4 =

11х2 + 4х – х2 – 4х = 10 х2

Упростите выражения, представьте многочлен в стандартном виде:

3х4 + 7х2 – 8х – 4х4 + 3х =

3ab2 +4 a3 – 5a2b – 3a3 – 9b2a =

12a – 8c – 7 + 3c – 12a=

2(n – 2) + 4m2 + 4 (n – 2)=

Умножьте: 2а( 6а – 5) = __________________

Заполните пропуски:

Чтобы умножить одночлен на многочлен, надо одночлен умножить на _________________________________________

Выполните умножение. Упростите:

- 4х(х2 + 2х -7) =

(2а2b – 4 a) · (- 1,5 ab)=

7(x – y) – 6(2x + 5y)=

Упростите:

4х - (х2 + 2х -7) =

2(0,1а – d) – (3,2a + 7d) =

- 2y – (y2 +4y – 9) – (y2 + 9) =

Выполните умножение. Упростите:

( 2- 4х)(2х -7) =

(а + 3)(а – 2)=

(x – y)(х + y) – (x2 + y2)=

ac

+dc

+bc

+bd

на каждое слагаемое другого

4х – 14 – 8х2 + 28х =

– 8х2 + 32х – 14

а2 – 2а + 3а – 6 =

а2 + а – 6

х2 + ху – ух – у2 – х2 – у2 =

- 2у2

При выполнении действий с минусом помни о знаке

Если минус перед скобкой, то при раскрытии их тяни минус до конца

2) (а + 3)- 4(а – 2)= 3) x2 - x(4 – x) =

4) (x – y) - (х +3y)(2х – у) – (2x2 +3y2 – 1)=

( 2- 4х)6 __ = 12у - ____; - 2ab( ___- 3b) = - 12 a2b2 + _____

5) 2ab(a -4) – 4(a2b + 2ab) =

Найдите значение выражения: х2 +2х + 18 - (х +6)(3 – 2х) при х = - 3

Найдите сумму значений многочлена х5 – 1,7х3 + 2,5 при х = 21,7 и х = - 21,7

2) 3)

4) Возведите в квадрат (а + b)2 =

( 2- 4х)х – 2(х+4) = 12 – 4х2
(0,5х +2)(7х – 0,21) = 0

5) Умножьте скобки (a – b)(a +b) =

Найдите значение выражения:

Решите уравнения: х2 = 4 2х2 = 18

1

1

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Решить уравнение – значит ____________________________________.

Уравнения, имеющие одни и те же корни называются ______________

Свойства равносильности

Если слагаемое перенести из одной части в другую, поменяв его знак, то получится уравнение ________________________________________

Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение ____________________ ________________________________________

Одинаковые слагаемые в обеих частях уравнения можно ____________

k - ___________________________________; b – ____________________________

Решение.
Используя второе свойство равносильности разделим обе части на k , получим

Чтобы найти неизвестное, надо ________________________________________
______________________________________________________________________

Х =

Решите уравнения

kx = b

Проверяйте: поменяли ли знак при переносе, привели ли подобные

Решите уравнение х-2(3х- ½ ) = 4х-8(3-2х)

-5х – 20х = -24 – 1

-25х = - 25

х = 1

-5х + 1 = 20х -24

Усвоим алгоритм действия

2. Свободный член разделить на коэффициент при неизвестном

!

1. Решите уравнение 8х - 1,5 = 3х - 8,7

Выполните пункты, заполните соответствующие строчки.

Поменяйте знак при переносе

36х-4(6х-2)+38=х+3(4-2х)

Решите уравнения:

0,36х – 0,3(0,4х – 1,2) = 0,6

0∙ х = b Решений нет.

2. Коэффициент при неизвестном и свободный член равны нулю. k = 0, b = 0.

0∙ х = 0, х – любое действительное число.

6(1,2х – 0,5) – 1,3х = 5,9х – 3

28 – 20х = 2х +25 – 22х – 12

Любое уравнение с дробями целесообразно привести к целому виду.

1. Умножьте обе части уравнения на НОЗ знаменателей

·

Теперь легко решить уравнение.

Это действие можно записать и выполнить короче.

2

2

3

3

6

2х – 3(х – 1) = 10х + 3х – 12

5. Решить уравнение

= 0

= 0

или

Решите уравнения:

( х – 3 )(2х +5 ) = 0

12х(х – 5 ) = 0

или

или

или

Ответ:

или

Ответ:

Уравнения с модулем

│а│ = а ,если а ≥ 0,

│а│ = - а , если а < 0.

а по модулю равно самому а ,если а больше или равно нулю; а по модулю равно противоположному а ( - а), если а меньше нуля.

Под а понимается любое выражение, например 2х -3 или х/2 +7 и т. д.

Решим уравнение: │х│ = 5
Так как │х│= х или │х│= -х, получим два уравнения
х = 5 или х = - 5 Ответ: ± 5

Решите уравнения:

| х – 3| = 0

12 |1 – 5x | = 0

или

или

или

Ответ:

или

Ответ:

3│5 – 2х│ - 4 = 5

или

или

Ответ:

______________

_____________

Так как a(b + c)

То ab + ac

= ______________

= ___________

Это

Это

Разложение на множители

= a(b + c)

Разделить каждое слагаемое на общий множитель

_________________________________
_________________________________

______________________

2х(4 -5х) = __________

8х – 10х2 = ___________

Что это?

Как это?

Умножить каждое слагаемое в скобке на множитель перед скобкой

4а(3 +2а2) = __________

с2 (4 -3с) = ___________

12а + 8а2 = ___________

4с2 – 3с3 = ___________

Общий множитель -

Впиши выражения в соответствующие фигуры и выполни разложение

=

+

а

2

3b

=

+

sinx

3

2

=

2. Выписать одинаковые множители;

3. Найти их произведение.

- это наибольший общий делитель (кратное) данных чисел

Для небольших чисел общий множитель можно найти устно:
подобрать общий делитель так, чтобы он был наибольшим

27 и 18

3·9 и 2·9

9

Найдите общий множитель. Вынесите общий множитель за скобку.

12х – 16у = __________________ 3) 15 с2 + 20 = __________________
36ab + 48c = _________________ 4) 54 x + 42a = _________________
5) 15b + 36c = __________________ 6) 36y – 72x = __________________

1. Разложить числа на простые множители;

2. Выписать одинаковые множители;

3. Найти их произведение.

Пример:

Справа пишите делитель

Слева пишите результат деления

Найдите наибольший общий множитель:

1) 140 и 84

НОМ = __________________

2) 180 и 135

НОМ = __________________

НОМ = __________________

40 = ______________

55 = ______________

Найдите общий множитель. Вынесите общий множитель за скобку.

140х – 84у = __________________ 4) 11 с2 + 55с - 363 = _______________
180a + 135 = _________________ 5) 4·0,85+8·0,075 = _________________
48b +40c+196 = __________________ 6) 12·0,3 – 8·0,4 = __________________
7) 1372 + 137·63 = ________________ 8) 122 – 288 = _____________________

Вывод

Вычисления производить проще, если можно вынести ОМ за скобку!

Это одинаковая буквенная часть в каждом слагаемом в меньшей степени

х, у

1

ху

Одинаковые буквы

Меньшая степень

Общий множитель

1. Разложите на множители

Запиши операции в соответствующие строчки

4a2 – 3a3b = ______( ______ - _______ 6x2y – 3xy3 = ______( ______ - _______

1. Разложите на множители

Запиши операции в соответствующие строчки

48a3 b2 – 36a2b3 + 30ab3 = ______( ______ - _______ + _______

Хочешь выполнять без ошибок? Проговаривай каждую операцию деления!

общий множитель
скобка

Результат деления

Выполните, проговаривая ключевые слова:

20х2у4 - 12х4у2 + 28х3у3 = _______________________________________
9х(х + 3)2 – 36х2(х + 3) = _______________________________________
4cosx – xcos3x = ______________________________________________

Выражение имеет скобки с противоположными выражениями.

Что это?

Нужно получить одинаковые скобки.

b(a – 1)

-

6(а – 1)

Чтобы скобки (а – 1) и (1 – а) преобразовать к одинаковому виду, надо __________
_________________________________________________________________________

Вынесение минуса за скобку

Вынесение минуса за скобку – это вынесение общего множителя, равного _______

Помните! 1 как множитель не пишется.

1. ______________________________________________

2. ______________________________________________

1.

2.

Вывод

При вынесении минуса получается выражение __________________________ данному

2 и ____

а и ____

a - b и - (_____)

-2 и ____

- а и ____

a - b и b_____

Запишите противоположные выражения:

Вынесите минус из подчеркнутого выражения:

4. Поставить минус перед всем выражением,
заключив его в скобки с противоположными
знаками (Вынести минус за скобку)

Поменять знаки у каждого
слагаемого в скобке

1)

6(а - 1) - b(a - 1) =

_____________________________________________

2) 6(а - 1) - b(1 - а) = _______________________________________________

3) 6(а - 1)2 + b(1 - а) = _______________________________________________

Чтобы не делать ошибок,

проговаривайте операцию деления: в 3) «а минус один в квадрате разделить на а минус один, будет а минус один»…

Разложите на множители :

1) 3(х – у)(х + у) – х + у = ____________________________________________________
2) 3(х – у)(х + у) – (х + у)2 = ___________________________________________________
3) (х – у)2 - 3( у - х) – х + у = __________________________________________________

*Разложите на множители :

Например, ab + 2a + 3b + 6

Разделим на две группы

Каждая группа содержит ОМ

При вынесении а получим: а(b + 2)

При вынесении 3 получим: 3(b + 2)

Такие выражения можно разложить на множители: надо общий множитель в виде скобки (b + 2) вынести за скобки.

Как это?

Расставьте по местам:

Квадрат
первого числа

Квадрат
второго числа

Удвоенное
произведение

(a + 2)2 = ___________________________________________

Возведите в квадрат, проговаривая операцию:

Квадрат суммы двух чисел
равен квадрату первого
числа, плюс удвоенное
произведение первого
на вторе, плюс квадрат
второго числа

Расставьте по местам:

Квадрат
первого числа

Квадрат
второго числа

Удвоенное
произведение

(a - 2)2 = ___________________________________________

Возведите в квадрат, проговаривая операцию:

Квадрат разности двух чисел
равен квадрату первого
числа, минус удвоенное
произведение первого
на вторе, плюс квадрат
второго числа

Возведите в квадрат:

Не забывать удвоенное произведение !

х2 – 2ху + у2

9а2 + 12ab + 4b2

х2 – 2х + 1

¼ a2 – 2a + 4

9а4 + 12a2 b4 + b8

4х2y2 – 4хy + 1

Вывод

(a – b)2=

Сравните: ( - a – b )2 = _______________________
(a + b)2 = __________________________

(- a – b)2=

Примените формулу, раскройте скобки:

Решите уравнение:

*Найдите 1/х2 + х2 , если а) 1/х + х = 4: _____________________________________
_________________________________________________________________________
б) 1/х + х = t: _____________________________________________________________
_________________________________________________________________________

2 место: _________________________;

3 место: ________________________;

Квадратный трехчлен

Квадрат
первого числа

Квадрат
второго числа

Удвоенное
произведение

1 место

3 место

2 место

a2 + 4b2 – 4ab = __________________________________

квадрат первого числа

удвоенное произведение

квадрат второго числа

а2

-4аb

+4b2

Стандартный вид квадратного трехчлена

2. Стандартный вид по знакам

+ + +

+ - +

или

Первое число а = _____

Второе число b = _________

Проверьте удвоенное произведение, запишите в виде (а ± b)2

x2 - 6х + 9 = ______________________

x

3

(x – 3)2

x

3

По квадрату второго числа найти число;

Записать выражение в виде (a ± b)2.

Проверить удвоенное произведение;

Привести выражение в стандартный вид;

Составьте

6m

±

2ab

n

6m

2

n

= (a + b)

2

6m

n

36m2 – 12mn + n2 = ___________________________________________________
x4 + 16 + 8x2 = _______________________________________________________
- 25a2 + 10ab – b2 = ___________________________________________________
½ y + 1 + ¼ y2 = ______________________________________________________

*Решите уравнения: 16х2 – 8х + 1 = 0 __________________________________
100 + 20х + х2 = 0 _______________________________________________________

*Выведите формулу ( a + b)3: ___________________________________________
______________________________________________________________________

x = ¼

x = - 10

разность

сумма

Разность квадратов двух чисел равна произведению разности
чисел на их сумму

Произведение разности чисел на их сумму равно
разности квадратов двух чисел

(a - b)(a + b) =

Решите уравнения:

(х – 1)(х + 1) = х2 – 2(х – 2) __________________________________________________
____________________________________________________________________________
(3х + 1)(3х + 1) – (3х – 2)(2 + 3х) = 17_________________________________________
____________________________________________________________________________

___________________________________________________________

____________________________________________________________

Решите уравнения, вычислите:

х2 – 4= 0__________________________________________________________________
9x 2 – 4 = 0 _____________________________________________________________
542 – 442 = ________________________________________________________________
252 – 122 = ________________________________________________________________

= (a + b)(a - ab + b )

2

2

= (a - b)(a + ab + b )

2

2

Разложите на множители, умножьте :

14am – 7an + 8bm – 4bn = __________________________________________________

б) группировка с общим множителем и ФСУ

х2 – у2 – 2х – 2у =__________________________________________________________

в) группировка с ФСУ

х2 + 2ху + у2 – 1 =__________________________________________________________

7а(2т – n) + 4b(2m – n) = (2m – n)(7a + 4b)

(x – y)(x + y) – 2(x – y) = (x – y)(x + y – 2)

(x + y)2 – 1 = (x + y – 1)(x + y + 1)

6(x3 + 1) = 6(x + 1)(x2 - 2 + 1)

7m(n2 – 4mn + 4m2) = 7m(n – 2m)2

(5x – 4)2

(3n – 2 – 1)(3n – 2 + 1) = (3n – 3)(3n – 1) = 3(n – 1)(3n – 1)

(a2 – 1)(a2 + 1) = (a – 1)(a + 1)(a2 + 1)

да

да

6(4х2 – 12х + 9 – у2)

ФСУ

= 6((2х – 3)2 – у2) = 6(2х – 3 – у)(2х – 3 + у)

да

= (х – 1 – (х2 +1)( х – 1 + х2 + 2)

= (х – х2 - 2)( х + х2 + 3)

ФСУ

(с – 1)2 - ( d + х)2 = (c – 1 – (d + x))( c - 1 + d + x)

= (c – 1 – d - x)( c - 1 + d + x)

sinx(2sinx – 1)

= x2 – x + 4x – 4

- x

+4 x

= x2 – x + 4x – 4

= x(x – 1) + 4(x – 1)

= (x – 1)(x + 4)

да

Как это?

Решение уравнений Уравнение вида произведение равно нулю

Произведение равно нулю, если ___________________________________________
_________________________________________________________________________

Решите уравнения:

Разложите на множители

Разложите на множители

Разложите на множители

х2 - х + 1 ≠ 0

Разложите на множители

Можно раскрыть скобки

Вычисления

Вычислите:

Сокращение дробей

1)


2)

Сократите дробь:

*

12 х2у – 180 ху2 – 30 х 3у3 = _________________________________________________
2) 12а(а –b) – 6b(a – b) = _______________________________________________________
3) x2(y – 7) – y2(7 – y) = ________________________________________________________
4) 3(a – 1)2 – 6a(1 – a) = _______________________________________________________

Вынесите общий множитель:

Разложите на множители:

12 х2у – 180 ху2 – 30 х 3у3 = __________________________________________________
2) 12а(а –b) – 6b(a – b) = _______________________________________________________
3) x2(y – 7) – y2(7 – y) = ________________________________________________________
4) 3(a – 1)2 – 6a(1 – a) = _______________________________________________________

1) 322 – 122 = ______________________________________________________________
2) 7∙ 28 – 19∙ 72 + 28∙ 72 – 7∙ 19 = _______________________________________________
3) 982 = ____________________________________________________________________
___________________________________________________________

Вычислите:

* Сократите дробь:

_________________________________________________________

_________________________________________________________

__________________________________________________________

Самоконтроль

Часть 1

Часть 2