- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по Организации кредитной работы на тему Расчет кредита (2 курс)
Содержание
- 1. Презентация по Организации кредитной работы на тему Расчет кредита (2 курс)
- 2. 1. Аннуитетные платежи представляют собой равные ежемесячные выплаты
- 3. Рассчитать ежемесячный платёж можно по формуле:гдеY – сумма
- 4. Например, банк дал Вам согласие на выдачукредита
- 5. Сумма ежемесячного платежа по кредиту составит:
- 6. Таких платежей за два года Вы совершите
- 7. Примерный план погашения кредита можно представить в
- 8. Слайд 8
- 9. Рассмотрим подробнее расчёты платежей за первый месяц.Как
- 10. Теперь рассмотрим второй тип платежей – дифференцированные
- 11. В нашем примере ежемесячная сумма погашения основного
- 12. Процентный платёж для первого месяца найдём по
- 13. Процентный платёж для второго месяца вычисляется по
- 14. Процентный платёж для четвёртого месяца вычисляется по
- 15. Общая формула для расчёта процентного платежа применительно к любому месяцу k будет иметь вид:гдеk = 1,…, m.
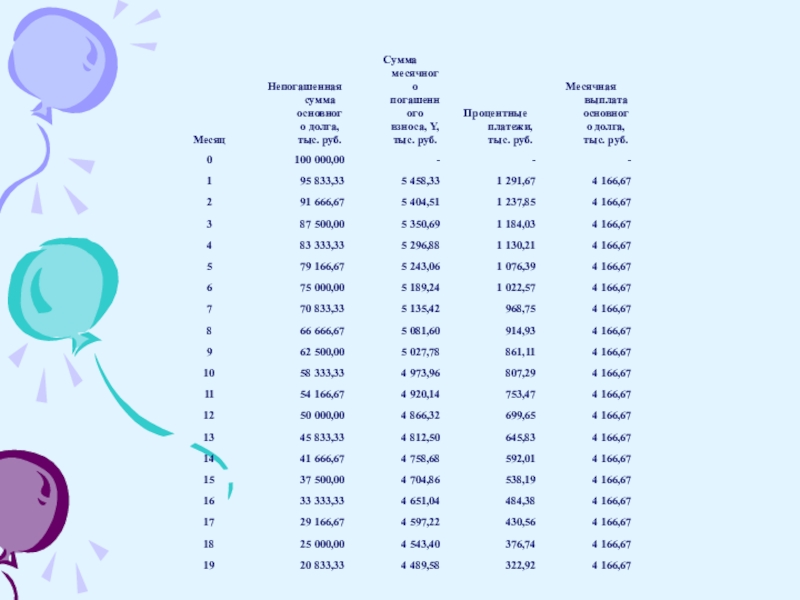
- 16. План погашения кредита при дифференцированных платежах будет следующий:
- 17. Слайд 17
- 18. Слайд 18
- 19. Как видно ежемесячные платежи в данном случае
1. Аннуитетные платежи представляют собой равные ежемесячные выплаты в течение всего срока кредитования. Значит, каждый месяц Вы будете платить банку одну и ту же сумму на протяжении всего срока (в нашем примере на протяжении двух лет).
Слайд 21. Аннуитетные платежи представляют собой равные ежемесячные выплаты в течение всего срока
кредитования.
Значит, каждый месяц Вы будете платить банку одну и ту же сумму на протяжении всего срока (в нашем примере на протяжении двух лет).
Значит, каждый месяц Вы будете платить банку одну и ту же сумму на протяжении всего срока (в нашем примере на протяжении двух лет).
Слайд 3Рассчитать ежемесячный платёж можно по формуле:
где
Y – сумма ежемесячного платежа,
D – сумма кредита
(основной долг),
i – процентная ставка, в коэффициентах (в нашем примере 0,155 = 15,5% / 100%),
m – число начислений процентов в течение года,
n – срок погашения в годах.
i – процентная ставка, в коэффициентах (в нашем примере 0,155 = 15,5% / 100%),
m – число начислений процентов в течение года,
n – срок погашения в годах.
Слайд 4Например, банк дал Вам согласие на выдачу
кредита в размере – 100
000 рублей,
по ставке – 15,5% годовых,
сроком на 2 года,
порядок погашения – аннуитетные платежи.
Найдём ежемесячный платёж,
а также рассчитаем переплату по кредиту.
по ставке – 15,5% годовых,
сроком на 2 года,
порядок погашения – аннуитетные платежи.
Найдём ежемесячный платёж,
а также рассчитаем переплату по кредиту.
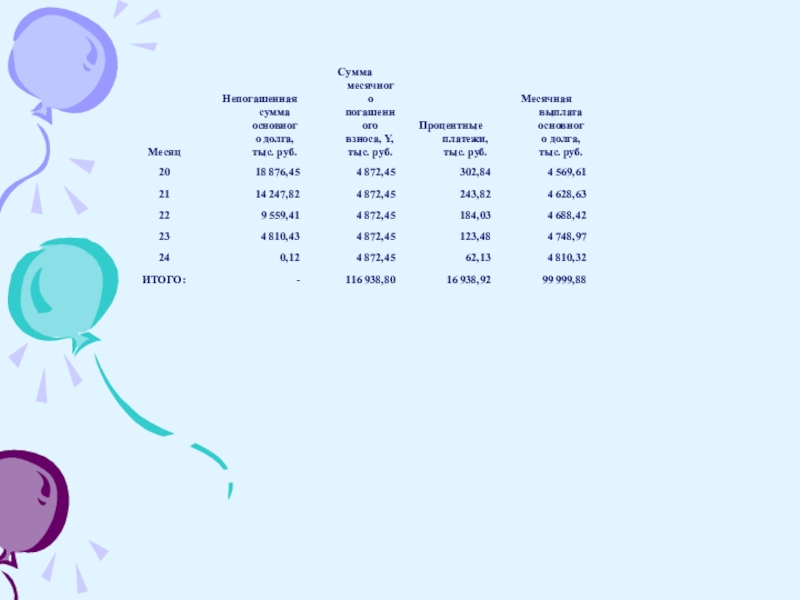
Слайд 6Таких платежей за два года Вы совершите 24 раза,
следовательно, всего
за два года будет выплачено:
4 872,45 × 24 = 116 938,9 рублей.
Теперь можно рассчитать переплату по кредиту
– из общей суммы платежей по кредиту вычесть сумму основного долга:
116 938,9 – 100 000 = 16 938,9 рублей
Вот такую сумму Вы заплатите банку за пользование кредитом
при погашении аннуитетными платежами.
4 872,45 × 24 = 116 938,9 рублей.
Теперь можно рассчитать переплату по кредиту
– из общей суммы платежей по кредиту вычесть сумму основного долга:
116 938,9 – 100 000 = 16 938,9 рублей
Вот такую сумму Вы заплатите банку за пользование кредитом
при погашении аннуитетными платежами.
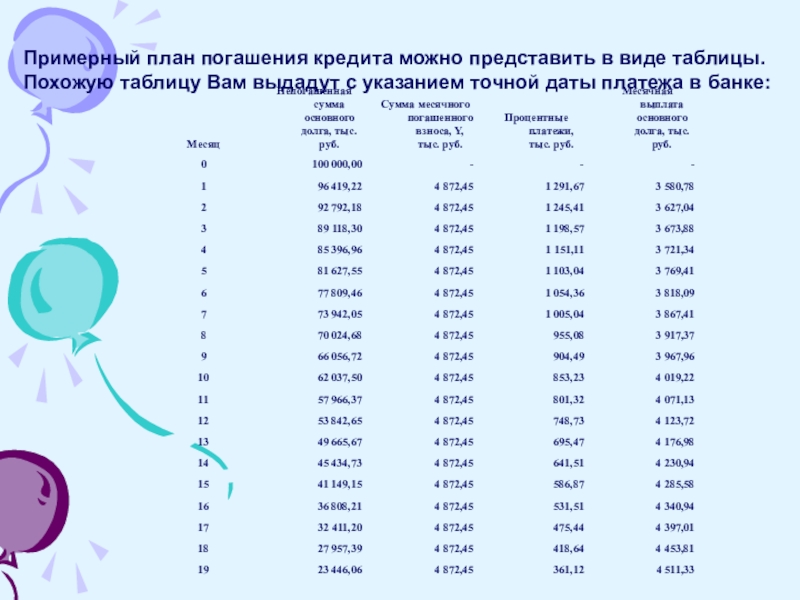
Слайд 7Примерный план погашения кредита можно представить в виде таблицы.
Похожую таблицу
Вам выдадут с указанием точной даты платежа в банке:
Слайд 9Рассмотрим подробнее расчёты платежей за первый месяц.
Как было подсчитано выше, сумма
ежемесячного платежа
равна 4 872,45 рубля.
Эта сумма включает процентный платёж,
который в первый месяц рассчитывается на всю величину долга:
100 000 × 0,155 / 12 = 1291,67 рубль
и месячную сумму основного долга:
4 872,45 – 1 291,67 = 3 580,79 рублей
На эту сумму уменьшится основная сумма долга.
Теперь основная сумма долга составит:
100 000 – 3580,79 = 96 419,21 рублей
Во второй месяц ежемесячный платёж остался прежним – 4 872,45 рубля,
а вот процентный платёж снизится, так как будет рассчитан
от величины оставшейся основной суммы долга:
96 419,21 × 0,155 / 12 =1 245,41 рублей
Соответственно на долю месячной суммы основного долга приходится
4 872,45 – 1 245,41= 3 627,04 рублей и т. д.
равна 4 872,45 рубля.
Эта сумма включает процентный платёж,
который в первый месяц рассчитывается на всю величину долга:
100 000 × 0,155 / 12 = 1291,67 рубль
и месячную сумму основного долга:
4 872,45 – 1 291,67 = 3 580,79 рублей
На эту сумму уменьшится основная сумма долга.
Теперь основная сумма долга составит:
100 000 – 3580,79 = 96 419,21 рублей
Во второй месяц ежемесячный платёж остался прежним – 4 872,45 рубля,
а вот процентный платёж снизится, так как будет рассчитан
от величины оставшейся основной суммы долга:
96 419,21 × 0,155 / 12 =1 245,41 рублей
Соответственно на долю месячной суммы основного долга приходится
4 872,45 – 1 245,41= 3 627,04 рублей и т. д.
Слайд 10Теперь рассмотрим второй тип платежей – дифференцированные платежи.
Дифференцированные платежи представляют собой неравновеликие
ежемесячные выплаты, уменьшающиеся в течение срока кредитования.
При этом весь долг делится на равные части и ежемесячная выплата основного долга не меняется.
При этом весь долг делится на равные части и ежемесячная выплата основного долга не меняется.
Слайд 11В нашем примере ежемесячная сумма погашения
основного долга будет равна:
где
D - величина
кредита,
m - число погасительных платежей в году,
n – срок погашения кредита в годах.
Рассчитаем ежемесячные процентные платежи.
m - число погасительных платежей в году,
n – срок погашения кредита в годах.
Рассчитаем ежемесячные процентные платежи.
Слайд 12Процентный платёж для первого месяца найдём по формуле:
Сумма платежа к погашению
за первый месяц
будет равна:
4 166,67 + 1 291,67 = 5458,34 рублей
будет равна:
4 166,67 + 1 291,67 = 5458,34 рублей
Слайд 13Процентный платёж для второго месяца вычисляется по формуле:
Сумма платежа к погашению
во втором месяце будет равна:
4 166,67 + 1 237,85 = 5 404,52 рубля
Процентный платёж для третьего месяца вычисляется по формуле:
Сумма платежа к погашению в третьем месяце будет равна:
4 166,67 + 1 184,03 = 5 350,7 рублей
4 166,67 + 1 237,85 = 5 404,52 рубля
Процентный платёж для третьего месяца вычисляется по формуле:
Сумма платежа к погашению в третьем месяце будет равна:
4 166,67 + 1 184,03 = 5 350,7 рублей
Слайд 14Процентный платёж для четвёртого месяца вычисляется по формуле:
Сумма платежа к погашению
в четвёртом месяце будет равна:
4 166,67 + 1 130,21 = 5 296,88 рублей
и т. д.
4 166,67 + 1 130,21 = 5 296,88 рублей
и т. д.
Слайд 15Общая формула для расчёта процентного платежа
применительно к любому месяцу k будет иметь
вид:
где
k = 1,…, m.
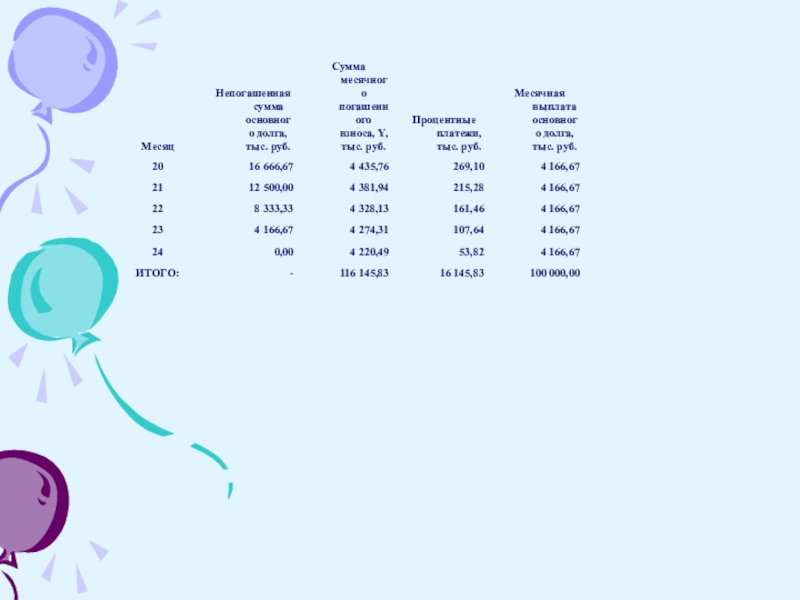
Слайд 19Как видно ежемесячные платежи в данном случае не равны
и с
каждым месяцем уменьшаются.
Переплата по кредиту при дифференцированных платежах
составила 16 145,83 рублей.
Как легко заметить, эта величина на 793,07 рубля меньше,
чем переплата при аннуитетных платежах
(16 938,9 рублей). Для кого-то эта разница покажется не существенной,
но при более высоких
цифрах кредита разница будет ощутима и сможет
очень здорово ударить по Вашему кошельку.
Итак, наиболее выгодным для Вас будет дифференцированный платёж.
Переплата по кредиту при аннуитетных платежах всегда выше, чем при
дифференцированных платежах, поэтому банки,
для достижения большей прибыли,
применяют в большинстве случаев именно
аннуитетные выплаты по кредиту.
Переплата по кредиту при дифференцированных платежах
составила 16 145,83 рублей.
Как легко заметить, эта величина на 793,07 рубля меньше,
чем переплата при аннуитетных платежах
(16 938,9 рублей). Для кого-то эта разница покажется не существенной,
но при более высоких
цифрах кредита разница будет ощутима и сможет
очень здорово ударить по Вашему кошельку.
Итак, наиболее выгодным для Вас будет дифференцированный платёж.
Переплата по кредиту при аннуитетных платежах всегда выше, чем при
дифференцированных платежах, поэтому банки,
для достижения большей прибыли,
применяют в большинстве случаев именно
аннуитетные выплаты по кредиту.