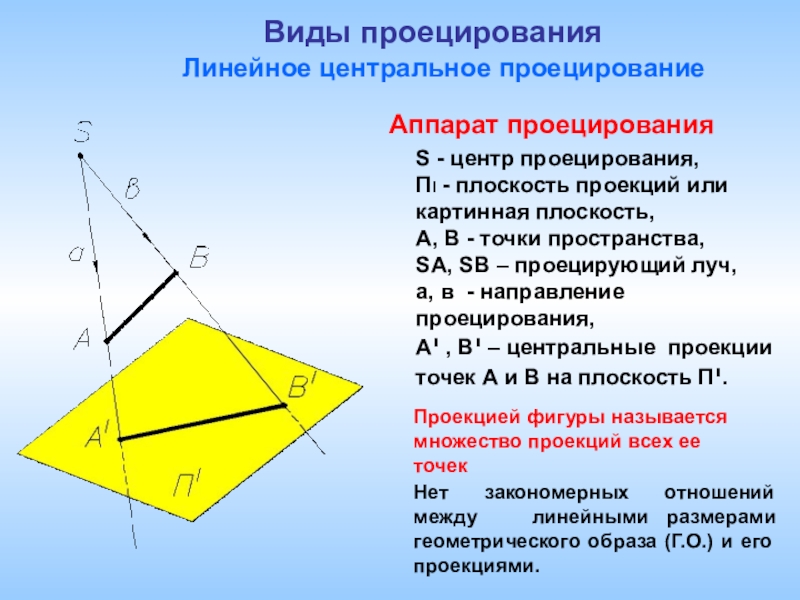
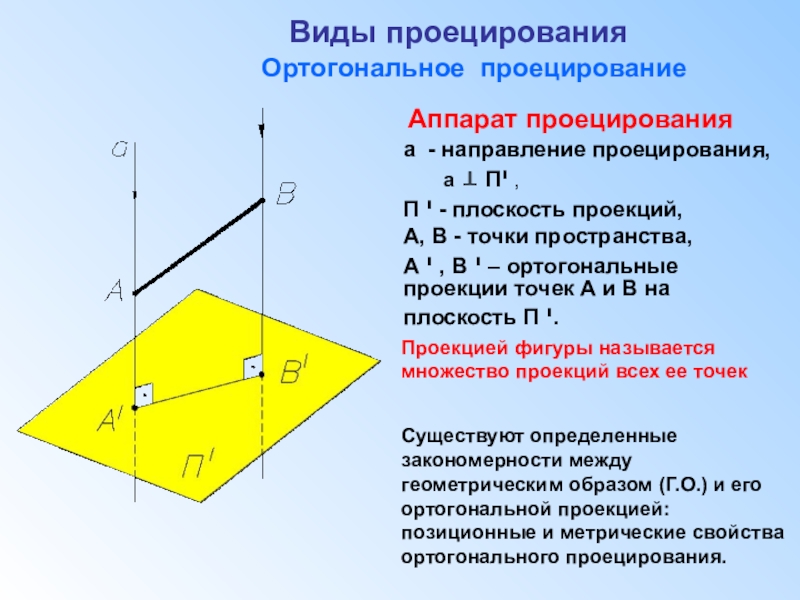
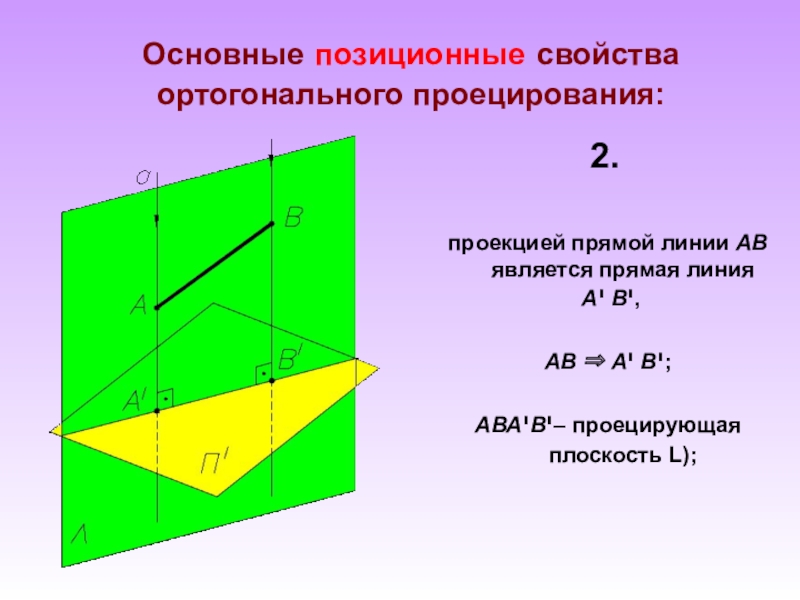
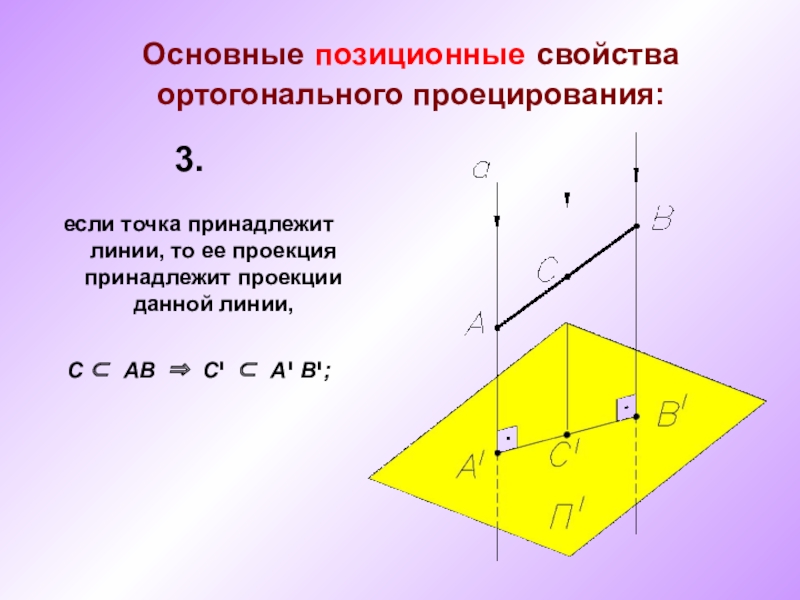
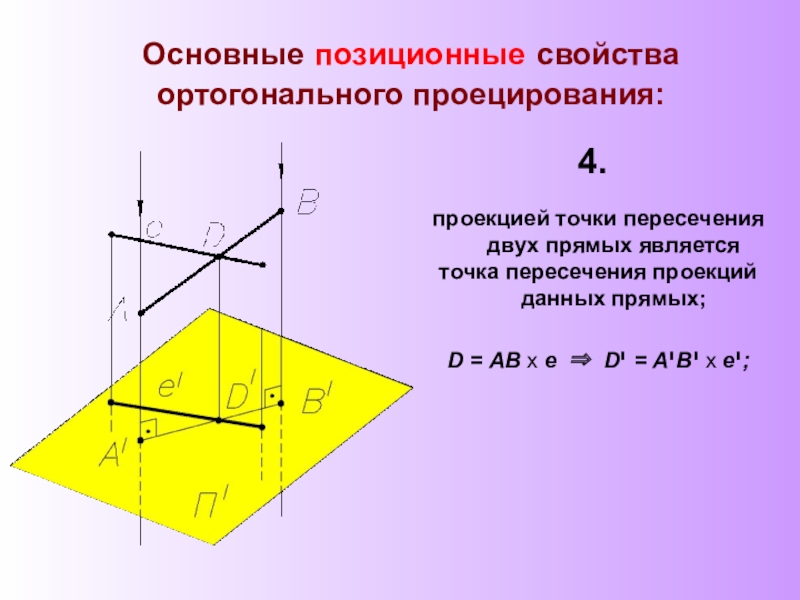
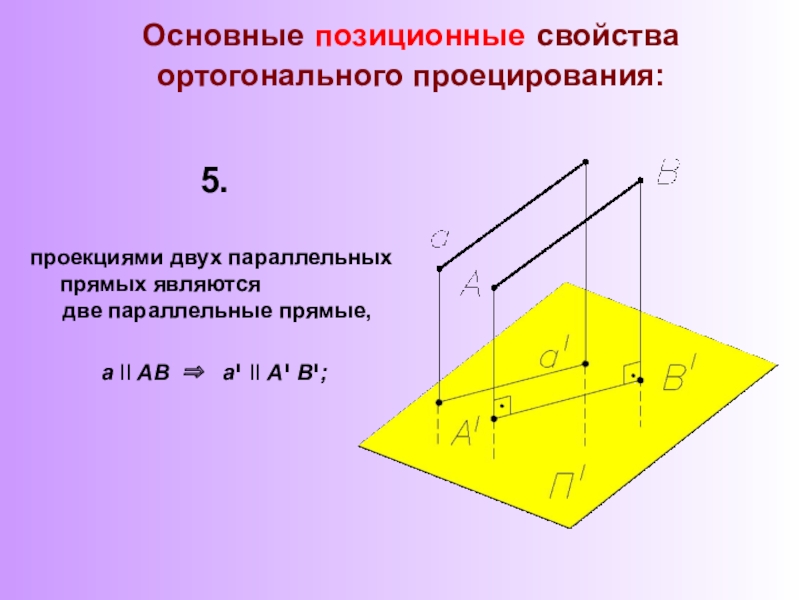
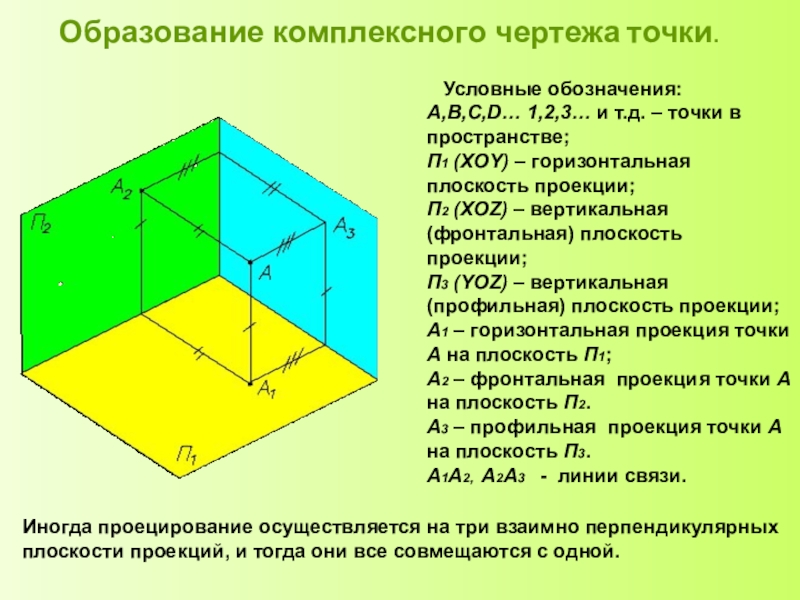
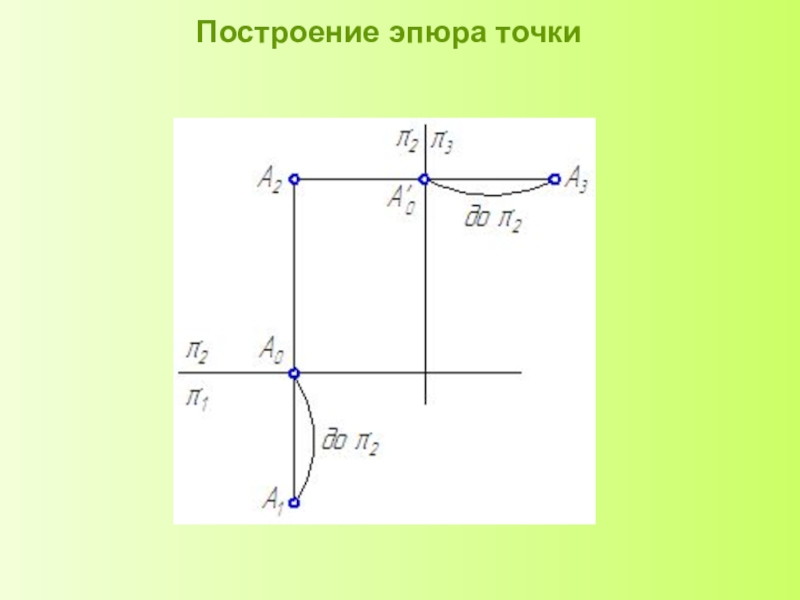
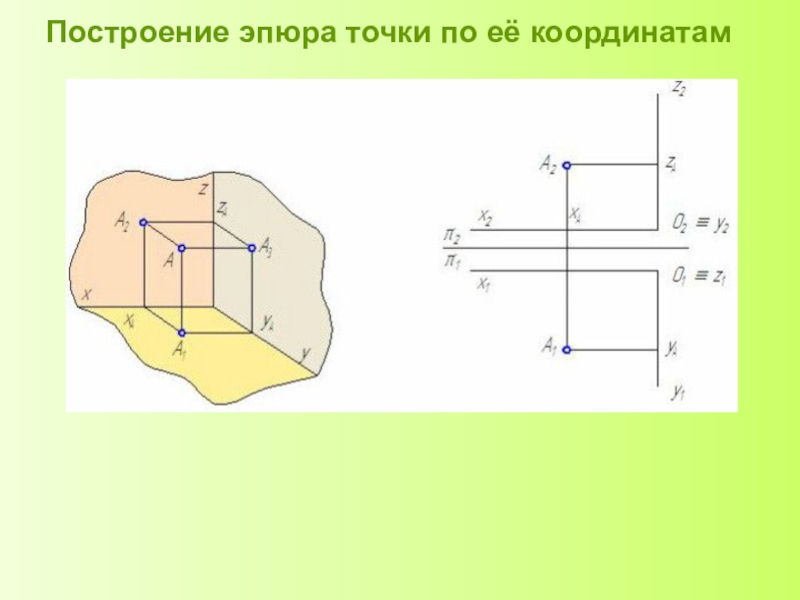
А, В - точки пространства,
SА, SВ – проецирующий луч,
а, в - направление проецирования,
Аי , Вי – центральные проекции точек А и В на плоскость Пי.
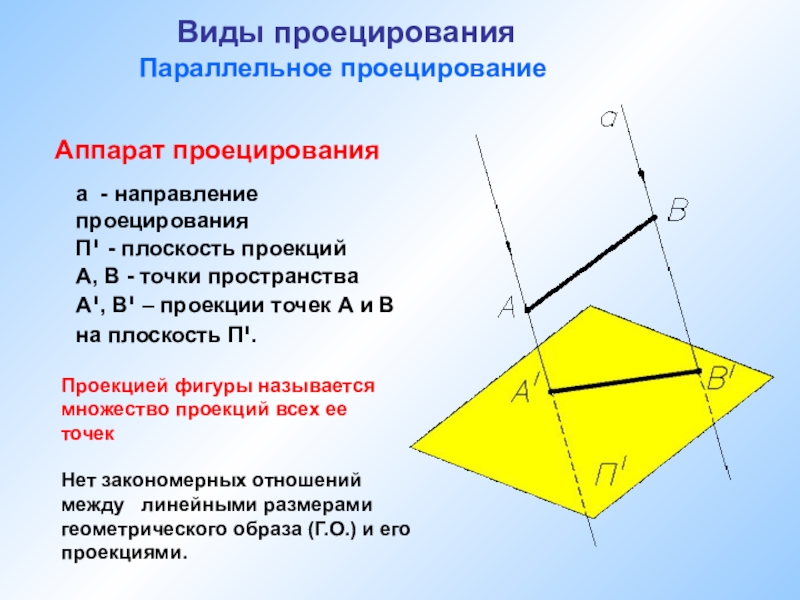
Аппарат проецирования
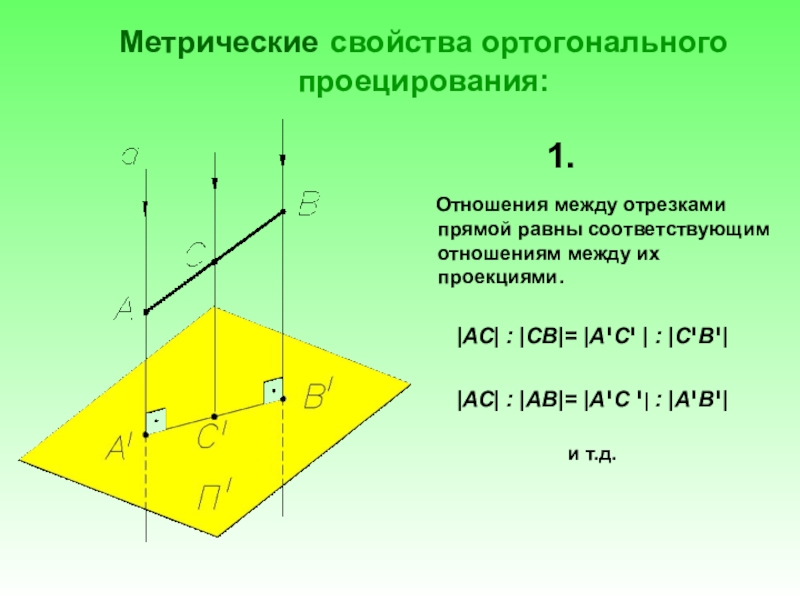
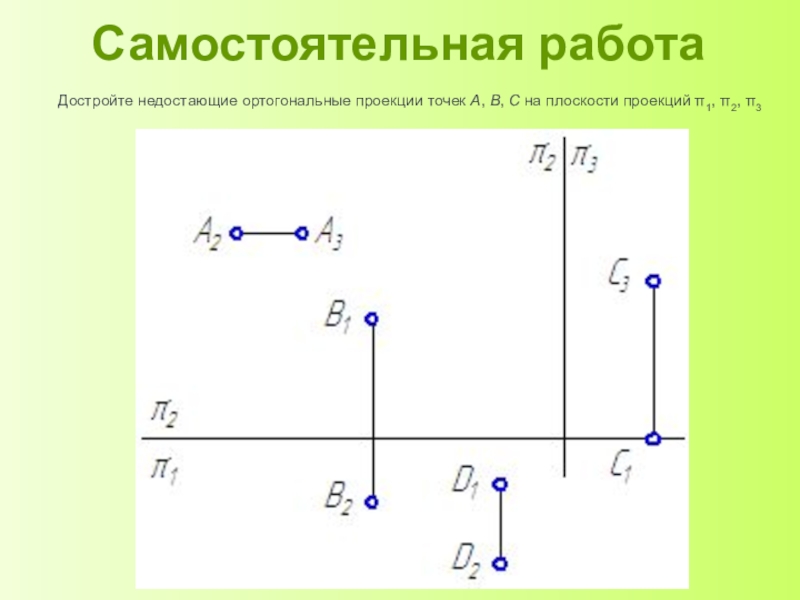
Проекцией фигуры называется множество проекций всех ее точек
Нет закономерных отношений между линейными размерами геометрического образа (Г.О.) и его проекциями.