- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к семинару на тему Интеграция как средство реализации ФГОС
Содержание
- 1. Презентация к семинару на тему Интеграция как средство реализации ФГОС
- 2. Слайд 2
- 3. ФЕДЕРАЛЬНЫЙ ГОСУДАРСТВЕННЫЙ ОБРАЗОВАТЕЛЬНЫЙ СТАНДАРТ Задача, которую
- 4. Ориентация образования на личность учащегося влияет на
- 5. Как составить и провести современный урок с
- 6. Переход на новые федеральные государственные образовательные стандарты требует
- 7. Противоречия в преподавании математики в Российской Федерации Комплексный
- 8. Мотивационные проблемы Низкая мотивация учащихся и студентов к
- 9. Мотивационные проблемы Проблема усугубляются тем, что сейчас значительная
- 10. Единые требования Единые требования к результатам обучения нереалистичны
- 11. Содержательные проблемы и неэффективность В погоне за
- 12. Из выше изложенного следует, что хуже всего
- 13. Для учащихся представляют определенную трудность «Текстовые задачи».
- 14. Учитывая вышеизложенное, приходишь к выводу, что учеников
- 15. Изучение предметной области «Математика и информатика» должно
- 16. Для проведения интегрированных уроков можно взять следующие
- 17. Интегрированный урок математики и информатики«Решение текстовых
- 18. Решите задачуЕсли от пункта А до пункта
- 19. Решение любой текстовой задачи складывается из трех
- 20. Объект -это любая часть окружающей нас действительности, воспринимаемая как единое целое.
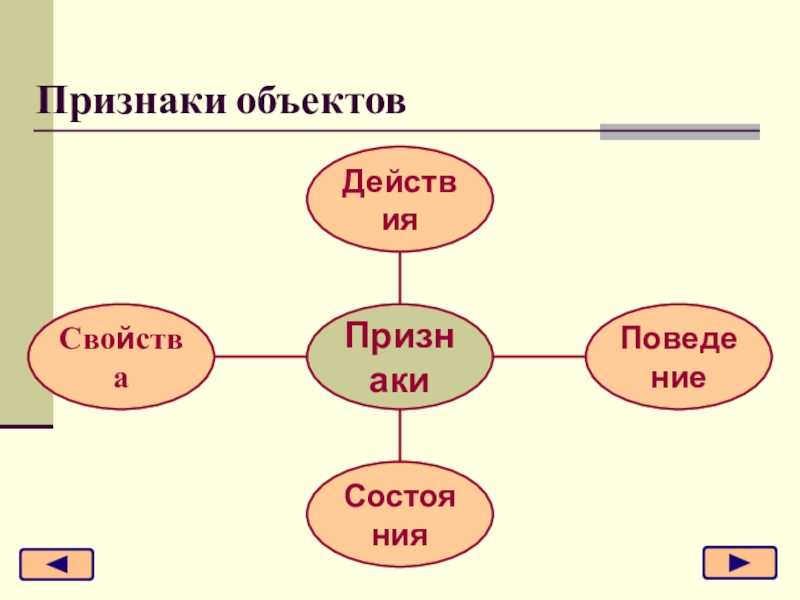
- 21. Признаки объектов
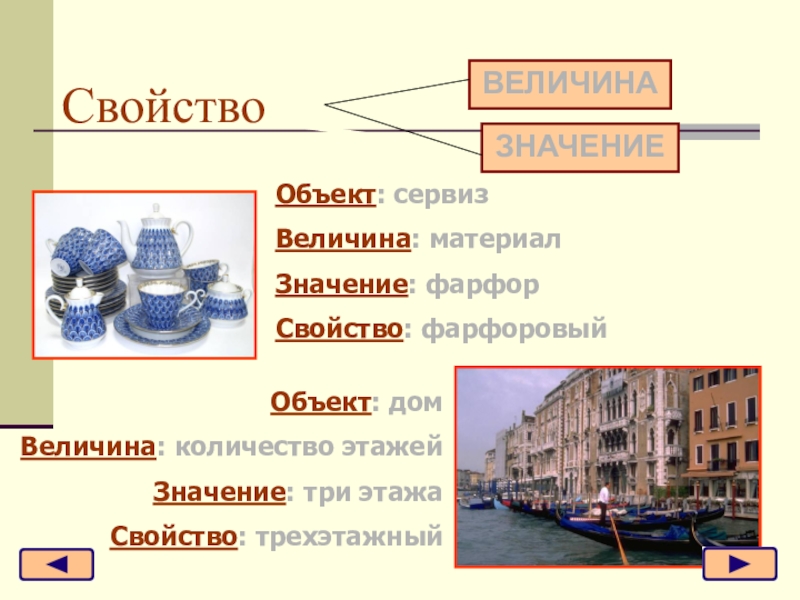
- 22. СвойствоЗНАЧЕНИЕВЕЛИЧИНА Объект: сервизВеличина: материалЗначение: фарфорСвойство: фарфоровыйОбъект: домВеличина: количество этажейЗначение: три этажаСвойство: трехэтажный
- 23. Отношение - определённая связь двух и более объектов
- 24. Родители присматривают за ребёнком
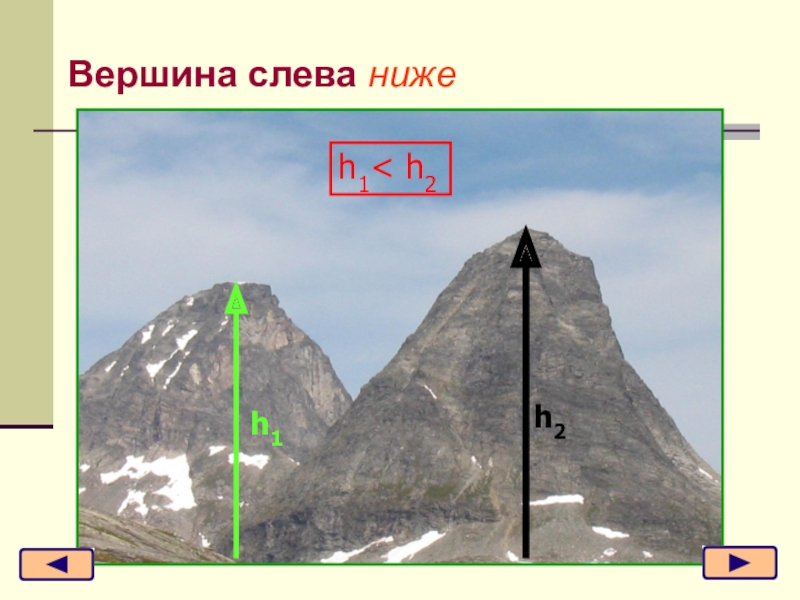
- 25. Вершина слева ниже h1h2h1< h2
- 26. Паром плывёт по заливу
- 27. Присматривают…Ниже…Плывёт…Отношения
- 28. Модель - это объект, который используется в
- 29. Алгоритм - модель деятельности исполнителя
- 30. Алгоритм -это предназначенное для конкретного исполнителя точное
- 31. Модели используются для:проверки гипотез и получения новых знаний об исследуемых объектах
- 32. Свойства моделейМодель отражает только часть свойств, отношений
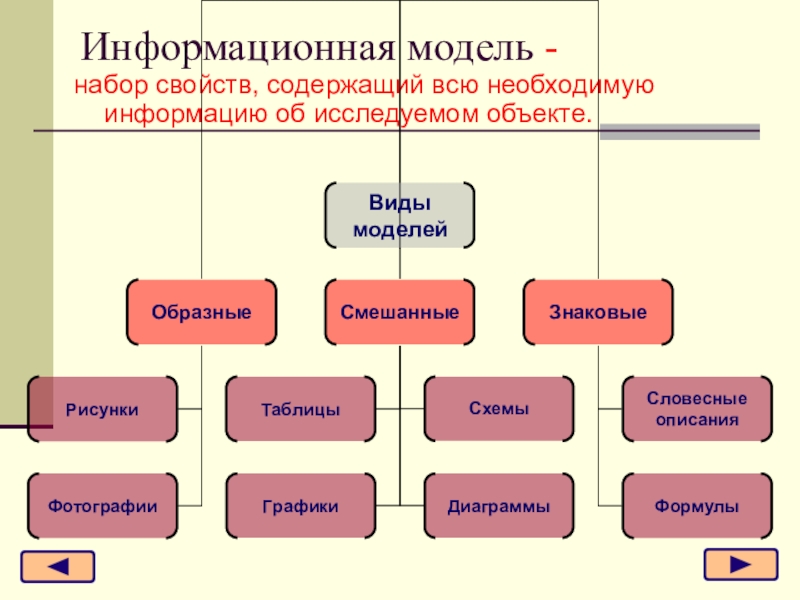
- 33. Информационная модель -набор свойств, содержащий всю необходимую информацию об исследуемом объекте.
- 34. Знаковые моделиЗнаковые информационные модели строятся с использованием различных языков (знаковых систем).
- 35. Табличные информационные модели
- 36. Таблицы вокруг насВычислительныеМедицинские
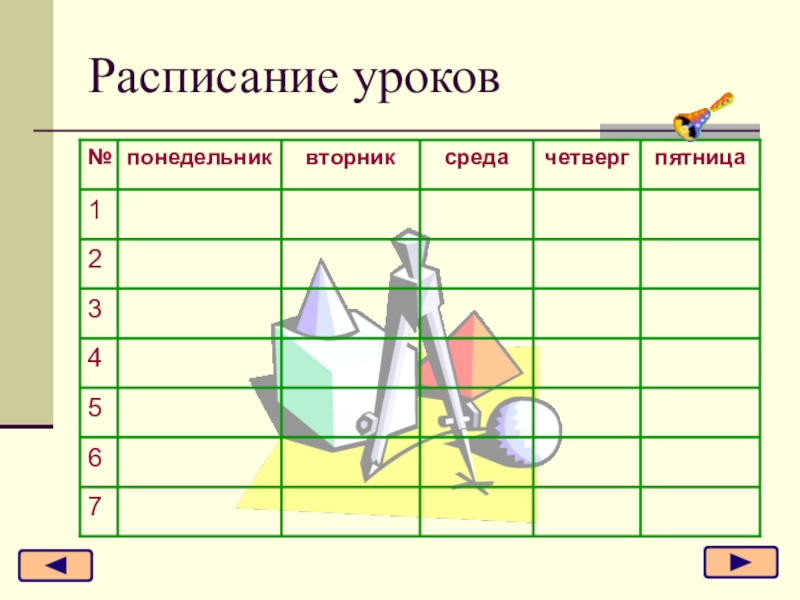
- 37. Расписание уроков
- 38. Таблица Д.И. Менделеева
- 39. Таблицы составляют для описанияряда объектов, обладающих одинаковыми наборами свойствУкажите объекты и одинаковые свойства объектов
- 40. Национальный костюмИнформация в таблице наглядна, компактна, легко обозрима.
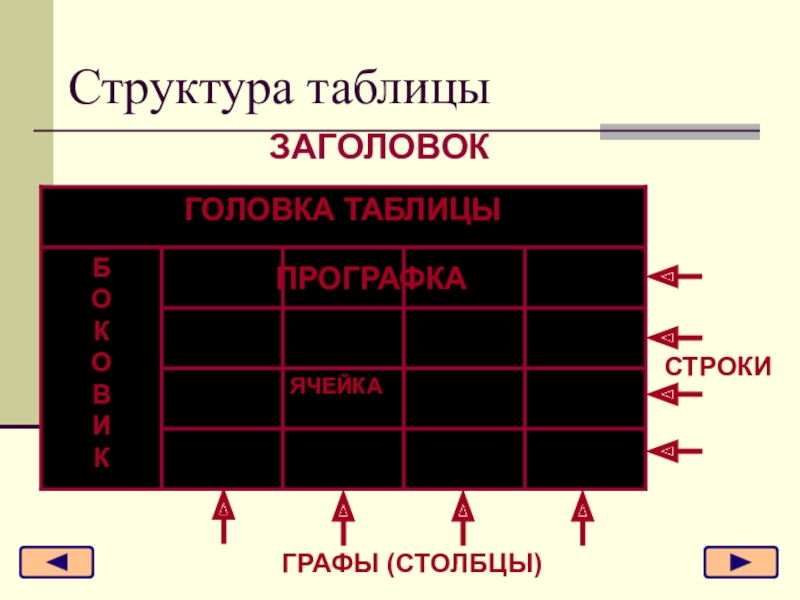
- 41. Структура таблицыПРОГРАФКАСТРОКИГРАФЫ (СТОЛБЦЫ)ЗАГОЛОВОК
- 42. Правила заполнения таблицыЗаголовок таблицы должен давать представление
- 43. Таблица состоит из столбцов и строк.Таблицы используют
- 44. Какие преимущества обеспечивают табличные модели по сравнению
- 45. Решите задачуЕсли от пункта А до пункта
- 46. Задание В13. В цилиндрическом сосуде уровень
- 47. Вопрос B14 Из А в В одновременно
- 48. ПослесловиеВ завершение необходимо отметить, что интегрированный подход
- 49. Какие положительные черты интегрированных уроков Вы можете
Слайд 1МБОУ СОШ №16 г.Белгорода
учитель информатики и математики
Пронина Р.И.
Интеграция
как
Слайд 3ФЕДЕРАЛЬНЫЙ ГОСУДАРСТВЕННЫЙ
ОБРАЗОВАТЕЛЬНЫЙ СТАНДАРТ
Задача, которую ставил перед собой великий педагог XVIII
Слайд 4Ориентация образования на личность учащегося влияет на принципы и формы педагогической
При реализации ФГОС
.
Задача обучения
сводится к организации условий, провоцирующих активную самостоятельную познавательную деятельность обучающихся.
Слайд 5Как составить и провести современный урок с учетом требований ФГОС?
Как научиться
научить детей добывать знания через собственную деятельность?
Слайд 6Переход
на новые федеральные государственные образовательные стандарты
требует дифференциации и интеграции содержания образования,
Интеграция – это не простое объединения частей в целое, это система, которая ведет к количественным и качественным изменениям.
Слайд 7Противоречия в преподавании математики в Российской Федерации
Комплексный анализ результатов образования, включая
Слайд 8Мотивационные проблемы
Низкая мотивация учащихся и студентов к приобретению математических знаний связана
Другая причина низкой мотивации –перегруженность школьной математики техническими элементами. У многих учащихся с 6 класса вырабатывается негативное отношение к математике как к непонятному и ненужному предмету, который невозможно освоить. Проблема усугубляется тем, что негативным отношением к математике проникнуто два-три поколения, поэтому в значительной части семей родители не могут поддержать учебную мотивацию учащихся.
Важным фактором, повлиявшим на падение учебной мотивации в последние 30 лет, является избыточная уравнительная ответственность, взятая на себя государством за процесс и результаты образовательной деятельности по отношению ко всем учащимся. Результат –формирование потребительского отношения к школе и отсутствие ответственности учащихся за результаты своего образования.
Мотивационные проблемы не исчезают с переходом в вуз: большинство российских вузов не формирует у студентов современные научные взгляды, не побуждает к исследованиям; карьера инженера, ученого и преподавателя непривлекательна.
Слайд 9Мотивационные проблемы
Проблема усугубляются тем, что сейчас значительная часть учащихся старших классов
предъявляет
метов повышенного внимания, а также предметы, «ненужные» с точки зрения дальнейшей учебы. Возникают противоречия в учебных интересах учащихся одного класса, где учитель не в со-
стоянии удовлетворить принципиально разные запросы, руководствуясь общим для всех образо-
ательным стандартом и программами.
Слайд 10Единые требования
Единые требования к результатам обучения нереалистичны для значительной части учащихся.
Слайд 11Содержательные проблемы и неэффективность
В погоне за необъятным и необоснованным содержанием
К окончанию 9 класса значительная часть учащихся (по разным оценкам от 20 до 40%) остается на уровне 5 – 7 классов. От 30 до 50% (в разных регионах) выпускников основной школы (9 класс) не готовы к дальнейшему обучению.
Слайд 12
Из выше изложенного следует, что хуже всего выпускники справляются с решением
Причиной является неумение прочитать условия задачи, правильно их понять и интерпретировать. 25% ошибок связаны именно с неправильной трактовкой условий.
Слайд 13
Для учащихся представляют определенную трудность «Текстовые задачи». 10% обучающихся к ним
Слайд 14
Учитывая вышеизложенное, приходишь к выводу, что учеников необходимо вооружить алгоритмом решения
Слайд 15Изучение предметной области «Математика и информатика» должно обеспечить:
умения моделировать реальные ситуации
овладение системой функциональных понятий, развитие умения использовать функционально-графические представления для решения различных математических задач, для описания и анализа реальных зависимостей;
развитие умений извлекать информацию, представленную в таблицах, на диаграммах, графиках;
формирование информационной и алгоритмической культуры;
формирование умений формализации и структурирования информации, умения выбирать способ представления данных в соответствии с поставленной задачей — таблицы, схемы, графики, диаграммы.
Слайд 16
Для проведения интегрированных уроков можно взять следующие темы:
информационное моделирование
математические инструменты, динамические
алгоритмы как инструмент решения задач с помощью компьютера.
Слайд 17Интегрированный урок
математики и информатики
«Решение текстовых задач с использованием технологии
информационного моделирования»
Дидактическая
Слайд 18Решите задачу
Если от пункта А до пункта В пешеход идет со
Если идет со скоростью 5 км/ч, то приходит на 6 минут раньше. Чему равно расстояние от А до В?
Слайд 19Решение любой текстовой задачи складывается из трех основных моментов:
Удачного выбора неизвестных.
Составления
Решения полученного уравнения.
Важно обязательно сформулировать при помощи переменной, ЧТО надо найти. Выбирая неизвестные, мы создаем математическую модель ситуации, описанной в условии задачи.
Слайд 22Свойство
ЗНАЧЕНИЕ
ВЕЛИЧИНА
Объект: сервиз
Величина: материал
Значение: фарфор
Свойство: фарфоровый
Объект: дом
Величина: количество этажей
Значение: три этажа
Свойство:
Слайд 28Модель - это объект, который используется в качестве «заместителя», представителя другого
Модель отражает только часть свойств, отношений и особенностей поведения оригинала.
Моделирование - процесс создания и использования модели.
Различают натурные и
информационные модели.
Модели объектов
Слайд 30Алгоритм -
это предназначенное для конкретного исполнителя точное описание последовательности действий, направленных
Алгоритм можно записать:
на естественном языке;
в виде нумерованного списка;
в виде блок-схемы.
Программа – это алгоритм, записанный по правилам понятного исполнителю языка.
Слайд 32Свойства моделей
Модель отражает только часть свойств, отношений и особенностей поведения оригинала.
Модель
форму;
цвет;
отдельные происходящие процессы
Не отражает:
реальные размеры;
многие происходящие процессы
Слайд 33Информационная модель -
набор свойств, содержащий всю необходимую информацию об исследуемом объекте.
Слайд 34Знаковые модели
Знаковые информационные модели строятся с использованием различных языков (знаковых систем).
Слайд 39Таблицы составляют для описания
ряда объектов, обладающих одинаковыми наборами свойств
Укажите объекты и
Слайд 42Правила заполнения таблицы
Заголовок таблицы должен давать представление о содержащейся в ней
Заголовки граф и строк должны быть краткими.
В таблице должны быть указаны единицы измерения.
Все ячейки таблицы должны быть заполнены. При необходимости в них заносят следующие знаки:
? – данные неизвестны;
× – данные невозможны;
↓ – данные должны быть взяты из вышележащей ячейки.
Слайд 43Таблица состоит из столбцов и строк.
Таблицы используют для описания ряда объектов,
Информация, представленная в таблице, наглядна, компактна, легко обозрима.
Самое главное
Слайд 44Какие преимущества обеспечивают табличные модели по сравнению со словесным описанием?
Любое ли
Приведите примеры таблиц, с которыми вы сталкивались в жизни.
Всегда ли удобно табличное представление информации?
Приведите пример знаковой информационной модели, рассматриваемой на уроках математики.
Модель каких отношений между людьми построена в басне И.А. Крылова «Волк и ягненок»?
Встречались ли вы с информационными моделями в жизненных ситуациях?
Давайте обсудим
Слайд 45Решите задачу
Если от пункта А до пункта В пешеход идет со
Если идет со скоростью 5 км/ч, то приходит на 6 минут раньше. Чему равно расстояние от А до В?
Слайд 46Задание В13. В цилиндрическом сосуде уровень жидкости достигает 48 см. На какой
Для решения задачи воспользуемся формулой вычисления объема цилиндра Vцилинда=πR2h, где R - радиус основания цилиндра, h - высота цилиндра.
B13
Весной катер идёт против течения реки в 123 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 112 раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
Слайд 47Вопрос B14 Из А в В одновременно выехали два автомобилиста. Первый проехал
В понедельник акции компании подорожали на некоторое число процентов, а во вторник подешевели на то же самое число процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник.
На сколько процентов подорожали акции компании в понедельник?
Заказ на 224 детали первый рабочий выполняет на 2 часа быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 2 детали больше?
Слайд 48Послесловие
В завершение необходимо отметить, что интегрированный подход на уроках математики создает
Слайд 49Какие положительные черты интегрированных уроков Вы можете отметить? Помогают ли такие уроки
насыщенность и информативность урока
насыщенность и визуальность
визуальность и связь с жизнью
информативность и связь с жизнью.