- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проектная работа по математике Эйлер-Венн
Содержание
- 1. Проектная работа по математике Эйлер-Венн
- 2. Цель исследования:изучение биографии Л. Эйлераизучение способа решения
- 3. Биография Леонарда ЭйлераЛеона́рд Э́йлер (нем. Leonhard Euler) родился 15 апреляапреля 1707, в городе
- 4. В 1726 году он был
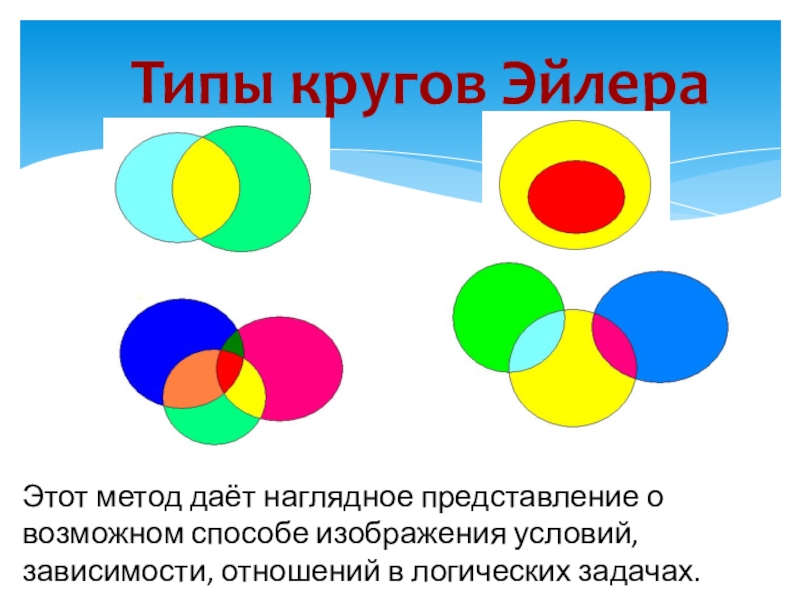
- 5. Типы кругов Эйлера Этот метод даёт наглядное
- 6. Любое множество А можно изобразить графически в
- 7. Знаки ∈ и ∉ a
- 8. e 8 b A 4На рисунке
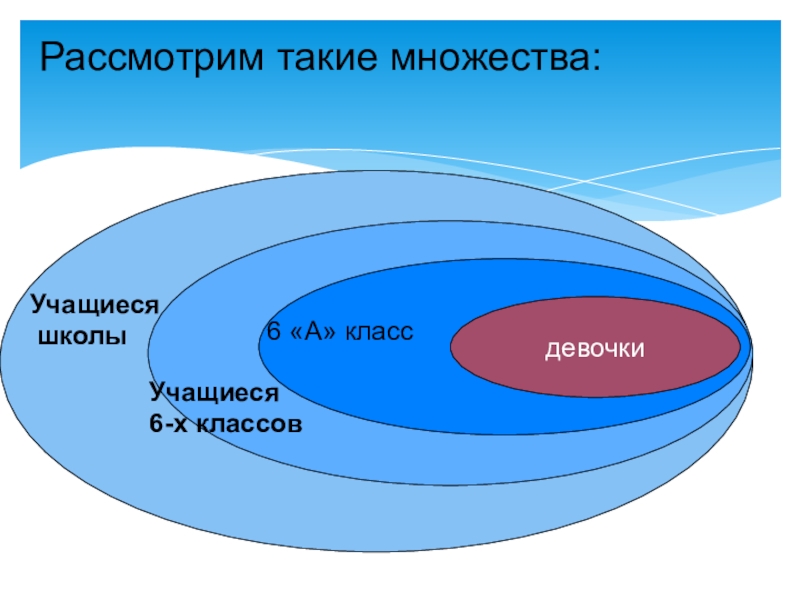
- 9. Учащиеся школыУчащиеся 6-х классов6 «А» классдевочкиРассмотрим такие множества:
- 10. Все мои друзья имеют какие-нибудь смартфоны. Шестеро
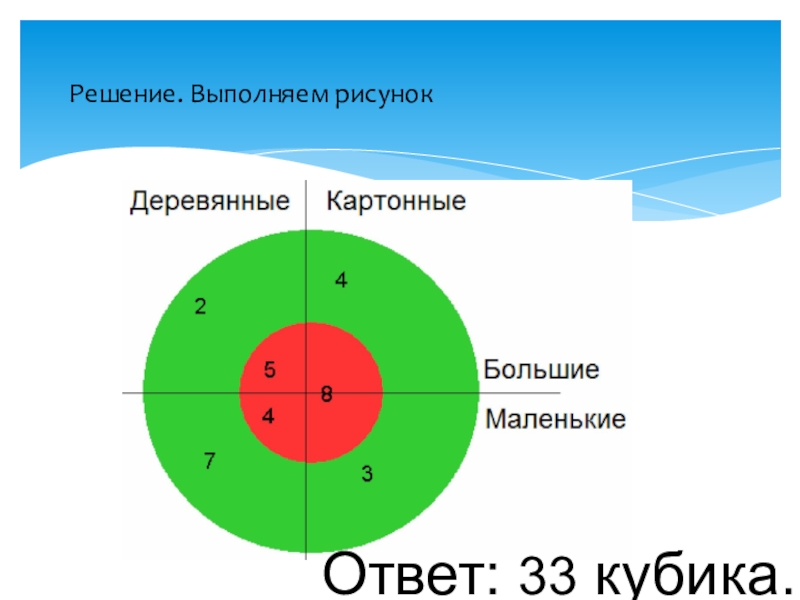
- 11. Ребятам поручили изготовить кубики. Несколько кубиков сделали
- 12. Решение. Выполняем рисунокОтвет: 33 кубика.
- 13. Задача №3 В классе 35 учеников. В
- 14. Слайд 14
- 15. На
- 16. Решение:1)12-( 5 +( 4-1,5) + (3-1,5-1))= 4м2
- 17. Всего – 30 человекПользуются метро – 20
- 18. троллейбус
- 19. Всего- 32 челБаскетбол - 16 челХоккей
- 20. Решение 32-3=29(ч) – играют хотя бы в
- 21. Ты человек, а значит, тыОбязан рассуждать –А
- 22. Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко
- 23. Выводы:Для решения задач, решаемых с помощью кругов
- 24. спасибо за внимание!
Слайд 1Диаграмма Эйлера-Венна
Работу выполнил ученик 6 класса «А»
МБОУСОШ №17 г.Тулы
Десяткина Павла
Классный рук-ль.:
Слайд 2Цель исследования:
изучение биографии Л. Эйлера
изучение способа решения задач с помощью кругов
Задачи исследования:
Познакомится с диаграммой Эйлера-Венна.
Составлять и решать подобные задачи.
Слайд 3Биография Леонарда Эйлера
Леона́рд Э́йлер (нем. Leonhard Euler) родился 15 апреляапреля 1707, в городе Базель, Швейцария. Швейцарский, немецкий и российский математик математик и механик математик и механик,
Слайд 4 В 1726 году он был приглашён работать в Санкт-Петербург.
Слайд 5Типы кругов Эйлера
Этот метод даёт наглядное представление о возможном способе изображения
Слайд 6Любое множество А можно изобразить графически в виде замкнутой линии.
Считается, что
Такая схема называется диаграммой Венна.
a
2
m
Например, диаграмму множества В = { 2, m, } можно нарисовать так:
В
Слайд 7
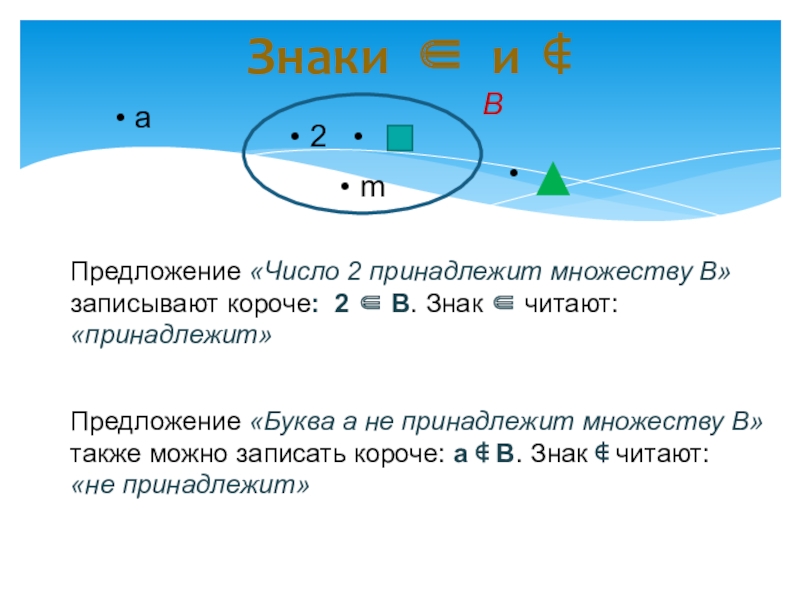
Знаки ∈ и ∉
a
2
m
Предложение «Число 2
Предложение «Буква а не принадлежит множеству В» также можно записать короче: а ∉ В. Знак ∉ читают:
«не принадлежит»
В
Слайд 8
e
8
b
A
4
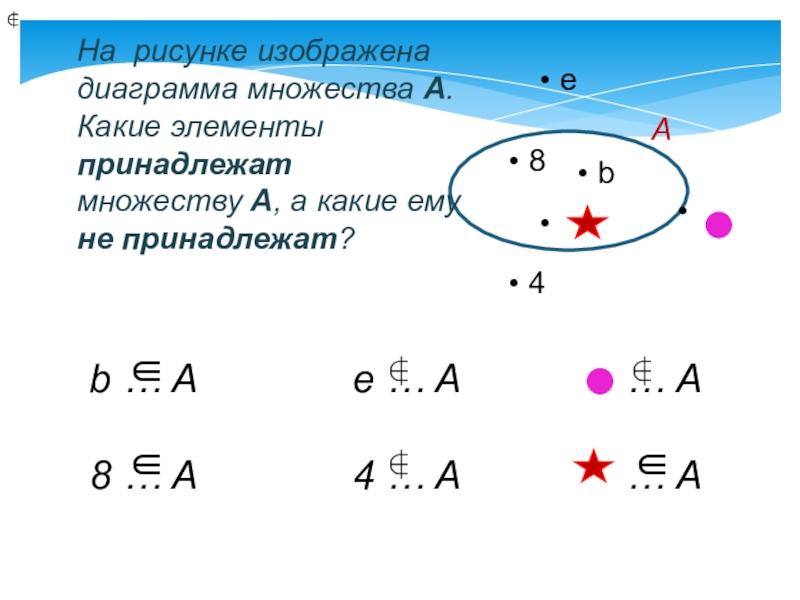
На рисунке изображена диаграмма множества
множеству А, а какие ему не принадлежат?
b … A e … A … A
8 … A 4 … A … A
∈
∈
∈
∉
∉
∉
∉
∉
Слайд 10Все мои друзья имеют какие-нибудь смартфоны. Шестеро из них имеют iPhone,
2
3
4
ОТВЕТ : 9 друзей
iPhone
Samsung
iPhone
Samsung
Задача №1
Слайд 11Ребятам поручили изготовить кубики. Несколько кубиков сделали из картона, а остальные
Задача, решаемая с помощью диаграммы Эйлера – Венна.
Задача №2
Слайд 13Задача №3
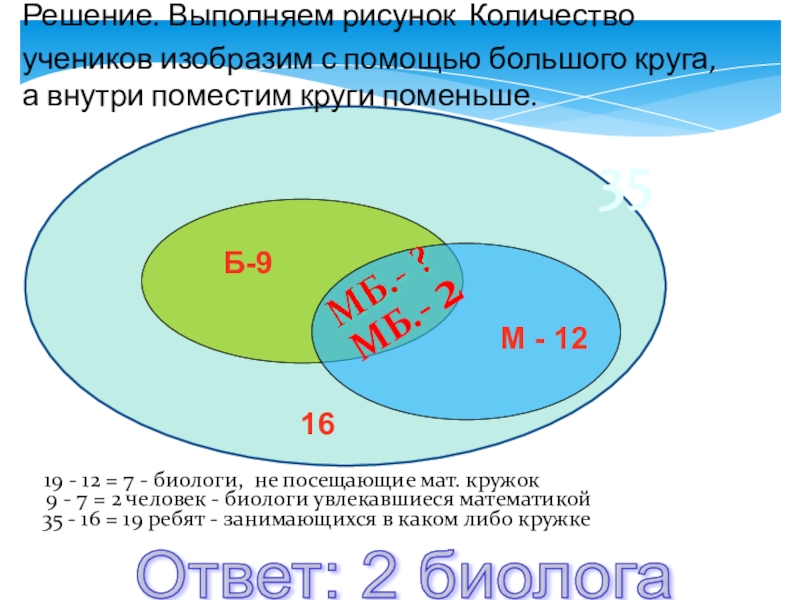
В классе 35 учеников. В математическом кружке из них
Слайд 14
35
35 - 16 = 19 ребят - занимающихся в каком либо кружке
9 - 7 = 2 человек - биологи увлекавшиеся математикой
Решение. Выполняем рисунок Количество учеников изобразим с помощью большого круга, а внутри поместим круги поменьше.
16
Б-9
М - 12
МБ.- 2
Ответ: 2 биолога
19 - 12 = 7 - биологи, не посещающие мат. кружок
Слайд 15
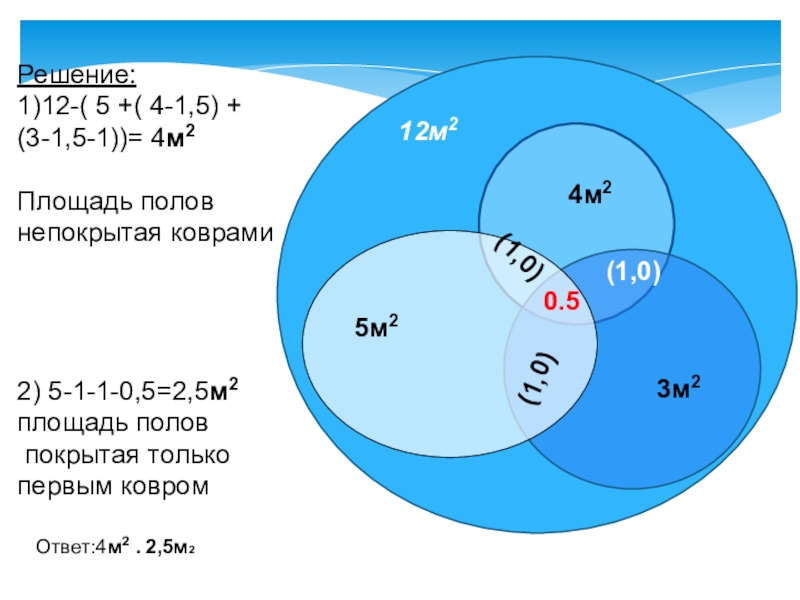
На полу площадью 12м2 лежат
Задача №4
Слайд 16Решение:
1)12-( 5 +( 4-1,5) + (3-1,5-1))= 4м2
Площадь полов
непокрытая коврами
2)
площадь полов
покрытая только первым ковром
Ответ:4м2 . 2,5м2
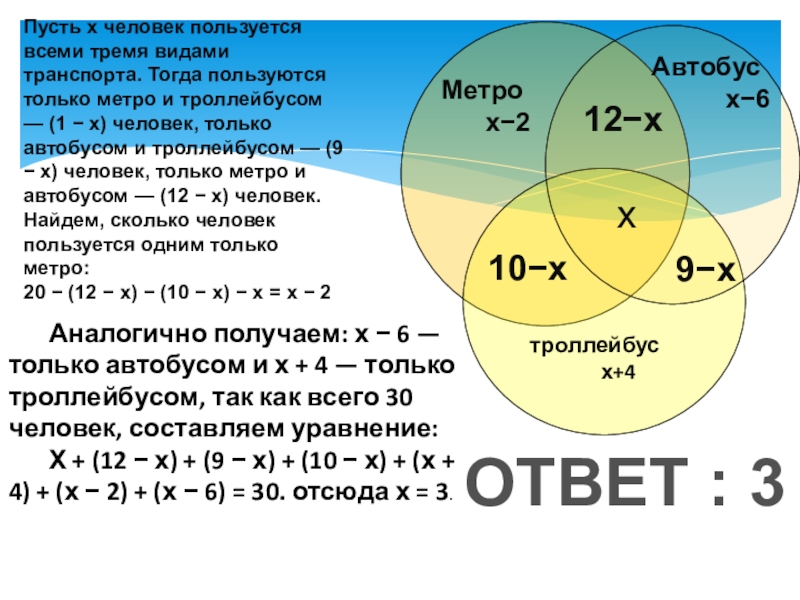
Слайд 17Всего – 30 человек
Пользуются метро – 20 человек
Автобусом – 15 человек
Троллейбусом
Метро и троллейбусом – 10 человек
Метро и автобусом – 12 человек
Троллейбусом и автобусом – 9
Сколько человек ежедневно пользуются всеми тремя видами транспорта?
Задача №6
Слайд 18
троллейбус
х+4
Автобус
Метро
х−2
х
10−х
9−х
12−х
Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом — (1 − х) человек, только автобусом и троллейбусом — (9 − х) человек, только метро и автобусом — (12 − х) человек. Найдем, сколько человек пользуется одним только метро:
20 − (12 − х) − (10 − х) − х = х − 2
Аналогично получаем: х − 6 — только автобусом и х + 4 — только троллейбусом, так как всего 30 человек, составляем уравнение:
Х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30. отсюда х = 3.
ОТВЕТ : 3
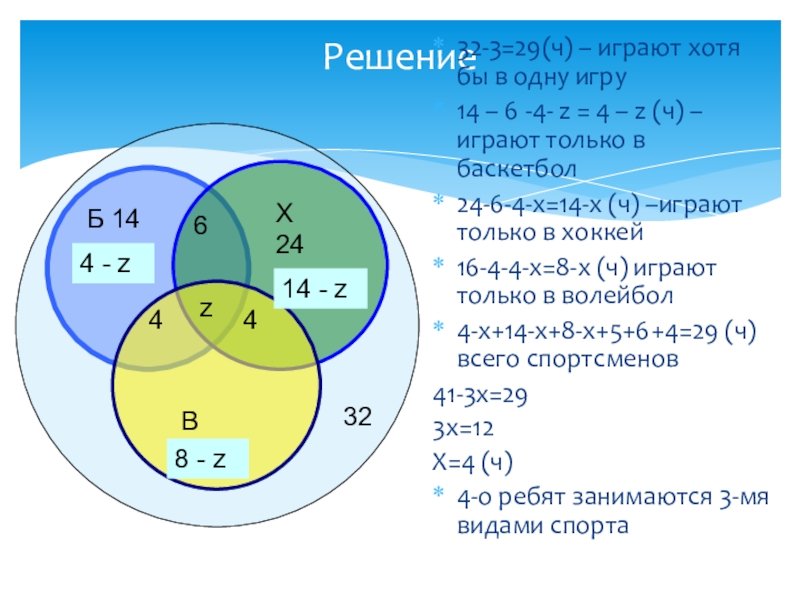
Слайд 19Всего- 32 чел
Баскетбол - 16 чел
Хоккей - 24
Волейбол - 16 чел
Б.Х - 6 чел
Б.В - 4 чел
В.Х - 4 чел
Ни чем– 3 чел
Сколько человек занимаются всеми видами спорта? В одной спортивной секции?
Задача №5
Слайд 20Решение
32-3=29(ч) – играют хотя бы в одну игру
14 – 6 -4-
24-6-4-х=14-х (ч) –играют только в хоккей
16-4-4-х=8-х (ч) играют только в волейбол
4-х+14-х+8-х+5+6+4=29 (ч) всего спортсменов
41-3х=29
3х=12
Х=4 (ч)
4-о ребят занимаются 3-мя видами спорта
Б 14
4 - z
Х 24
14 - z
В 16
8 - z
6
z
4
4
32
Слайд 21Ты человек, а значит, ты
Обязан рассуждать –
А без логичной простоты
Ты будешь
Пусть за собой она зовёт –
Уйми в коленях дрожь!
Коль с Логикой пойдёшь вперёд –
Нигде не пропадёшь!
(С. Алдошин)
заключение
Слайд 22Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным
Выводы
Слайд 23Выводы:
Для решения задач, решаемых с помощью кругов Эйлера, был составлен алгоритм,
Записываем краткое условие задачи.
Выполняем рисунок.
Записываем данные в круги (или в диаграмму Эйлера).
Выбираем условие, которое содержит больше свойств.
Анализируем, рассуждаем, не забывая записывать результаты в части круга (диаграммы).
Записываем ответ.