Презентация, доклад к семинару Развитие творческих способностей обучающихся в математике

ее.
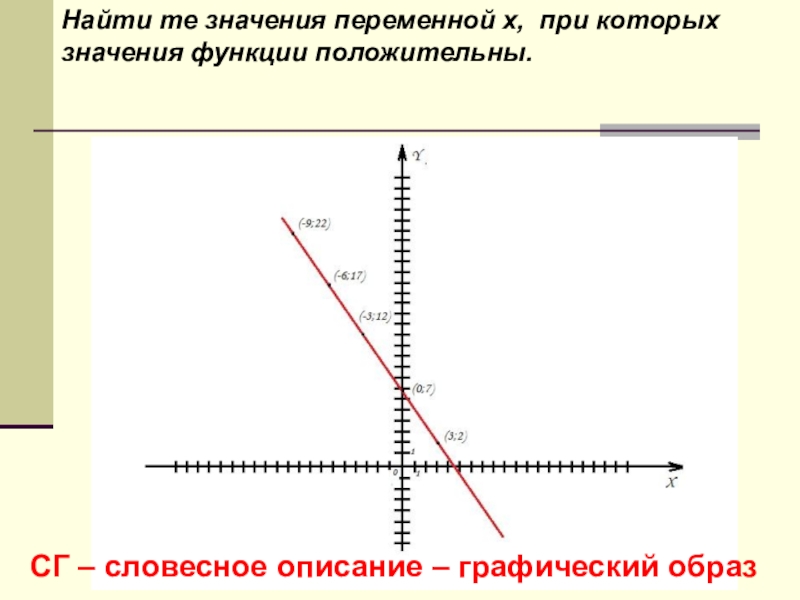
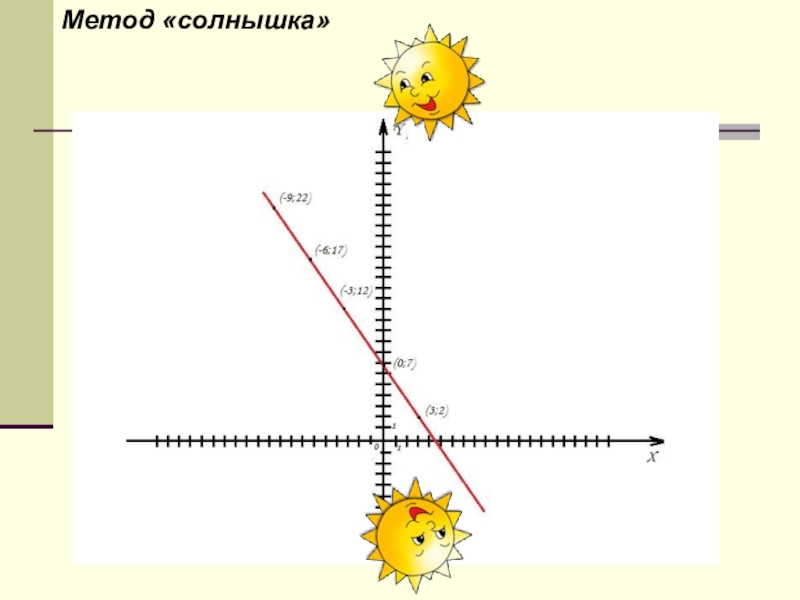
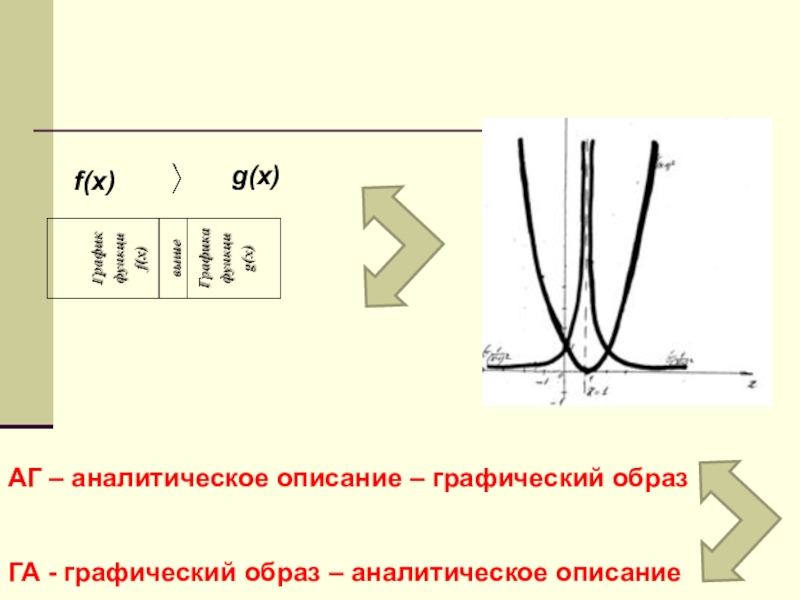
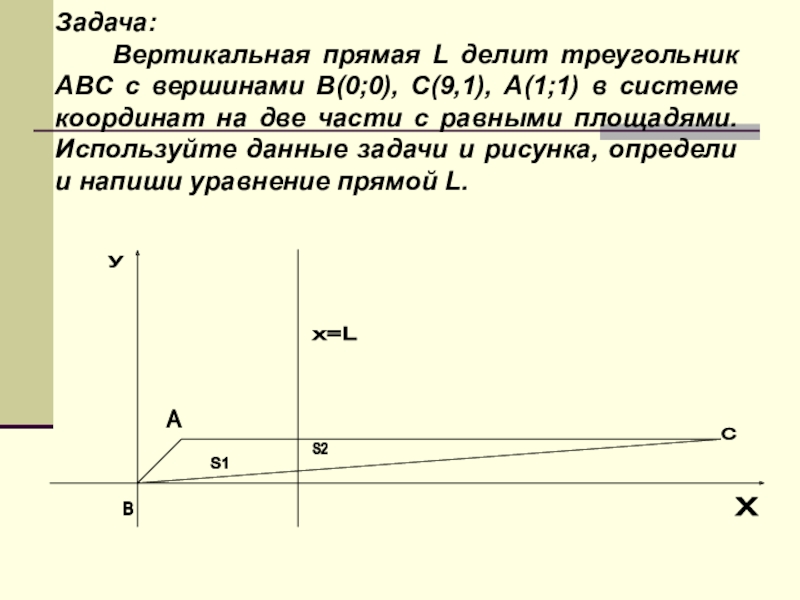
Если вы дадите ему рыбу, то поможете только один раз,
а если научите ловить, то накормите на всю жизнь!»

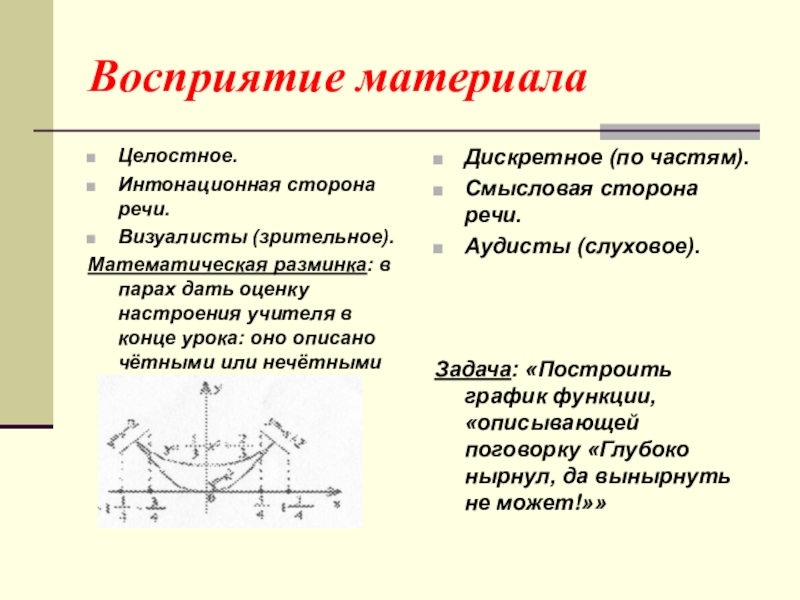
К рассмотрению стратегий осуществления деятельности можно применить, как минимум, четыре различных варианта:
·        Дать рыбу и не обучать ловле.
·        Учить голодного ловле.
·        Накормить, а потом учить ловле.
·        Учить ловле и одновременно кормить.

его построения: для чего (цели и ценности), чему (содержание) и как (технологии) необходимо учить подрастающее поколение.

(в рамках универсальных и общепринятых), благодаря которым люди способны прогнозировать многие явления, процессы и события, происходящие в объективной реальности. Эти стратегии выражены в специфическом языке описания конкретной науки, особенностях его построения, комплексе базовых понятий, опыте организации исследовательской деятельности и научных традициях.

стратегий познания мира. Последнее должно стать серьезным предметом междисциплинарных исследований.

но и от выбора адекватных инструментов их усвоения и передачи.

как существующие понятия почти не касаются динамического описания именно индивидуальной познавательной деятельности на операциональном уровне.

степени касаются действий внутреннего и внешнего планов.

процессов, что существенно для организации обучения на микротехнологическом уровне.

язык аналитических выражений (А);
язык графических изображений, «графический язык» (Г). При решении задач графического содержания возникает необходимость осущесвлять преобразование входной информации (условия задач) с языка, на котором она была задана, на язык, предполагаемый в ответе к задаче. Задачи графического содержания в соответствии с возможным сочетанием языков выражения условия и ответа разбиваются на пять классов. (Первая буква в обозначении класса показывает язык, на котором выражено условие задачи, а вторая – язык, на котором должен быть выражен ответ.)
1).СГ – словесное описание – графический образ;
2).АГ – аналитическое описание – графический образ;
3).ГС – графический образ – словесное описание;
4).ГА – графический образ – аналитическое описание;
5).ГГ – графический образ – графический образ.

деятельности

Преподавание – пре-подавание – начинается тогда, когда мы начинаем ощущать, воспринимать предмет сердцем, глазами ученика.

словесное описание – графический образ

аналитическое описание

f(x)

g(x)

1 2

ах-ах-ах(1) ах-ах-ах(2)

1 2

Естественный, словесный язык (С)

значит освободить его от принуждения и стереотипов, но прежде всего это предполагает его подготовку к жизни, которая будет постоянно требовать от него проявления способности к самостоятельному мышлению, умению вести дискуссию, изначально допуская, что не существует единственного ответа или единственно правильного решения.

способность догадываться, угадывать заранее результат, способность разумно искать правильный путь в самых запутанных условиях.
Прочтя задачу и ещё не произведя никаких действий, мы должны стремиться к тому, чтобы научиться сразу видеть, что тот или иной способ непригоден для её решения, а вот какой-то другой способ может быть использован. Такое умение вырабатывается в процессе решения одной и той же задачи разными способами. Именно поэтому часто полезнее решить одну задачу тремя различными способами, чем решить три – четыре различные задачи.

вершинами B(0;0), С(9,1), А(1;1) в системе координат на две части с равными площадями. Используйте данные задачи и рисунка, определи и напиши уравнение прямой L.

помощью
определителя

III способ.
С помощью геометрии

заполучить царство?»

«Нестандартное решение задач оптимизации».

фон.
Речевой и музыкальный ритм.

«Левополушарные»
учащиеся
Технология.
Детали.
Абстрактный линейный стиль изложения информации.
Неоднократное повторение учебного материала.
Тишна на уроке.

настроения учителя в конце урока: оно описано чётными или нечётными функциями и почему?

Дискретное (по частям).
Смысловая сторона речи.
Аудисты (слуховое).



Задача: «Построить график функции, «описывающей поговорку «Глубоко нырнул, да вынырнуть не может!»»

методами,
технологии проблемного обучения (исследовательская, критического мышления …) с технологией целенаправленного развития познавательных стратегий.

познание, для выявления глубоких связей, существующих между деятельностью и мыслью».

Б.В. Гнеденко

и воспитывали:

«Нет плохих учеников, есть плохие учителя»: