Буденновск
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Истина
Содержание
- 1. Презентация по теме Истина
- 2. Статистика-вещь серьезная. С ней-не поспоришь! Мы решили
- 3. Математики о производной. «
- 4. Физики о производной. «
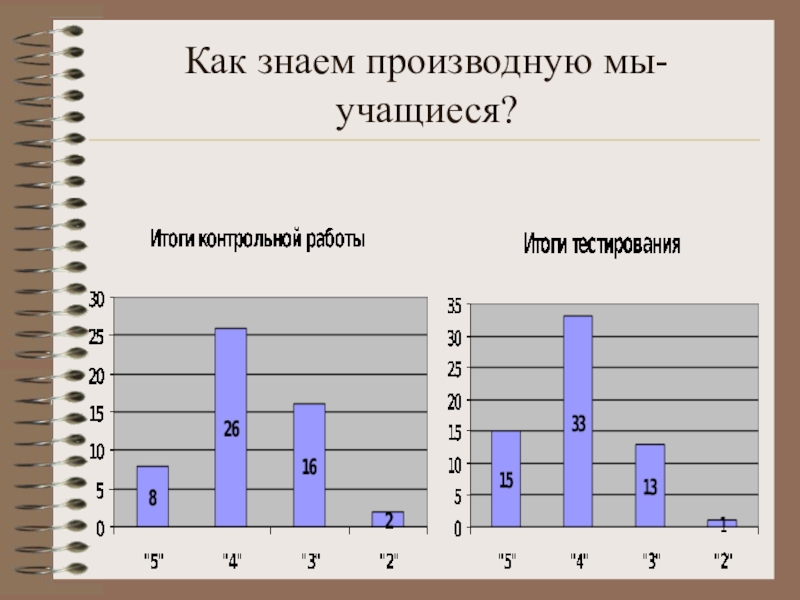
- 5. Как знаем производную мы-учащиеся?
- 6. Как часто в
- 7. Производная используется при решении следующих заданий:
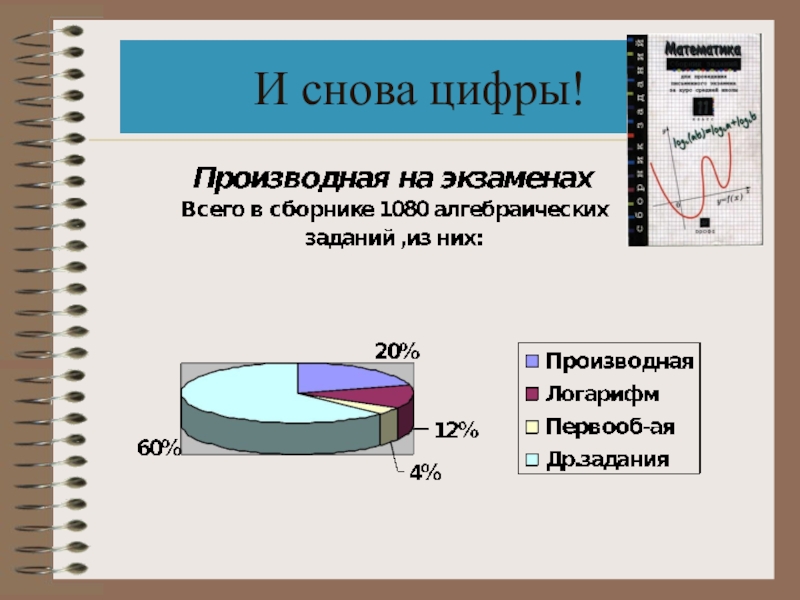
- 8. И снова цифры!
- 9. Поступление в ВУЗы
- 10. Вывод. В школьной программе
- 11. История великих открытий.Часть вторая.
- 12. Их, великих, загадочность окружающего мира притягивала, а
- 13. О великом Ньютоне! Был этот
- 14. О Лейбнице. «Предупреждаю,
- 15. Но это не говорит о том, …
- 16. Последователи учений Ньютона и Лейбница.
- 17. Вывод:Ньютон и Лейбниц, решая практические задачи в
- 18. Интриги в стране
- 19. Исследуя функции, мы встретились со случаями, когда
- 20. Взгляд из детства.Всем с детства известно такое
- 21. При отскоке от пола (при h=0)направление движения
- 22. Точки, в которых производная не существует, являются особыми точками.
- 23. Примеры функций, имеющих особые точки. Все функции
- 24. производнаяПри х=0 производная не существует (обращается в бесконечность), касательная становится вертикальной, х=0 является особой точкой.У функции
- 25. К числу особых точек относятся точки разрыва самой функции.
- 26. Наличие особых точек затрудняет исследования функции. Например:
- 27. Вывод.Окружающий мир очень сложен.И какие бы процессы
Статистика-вещь серьезная. С ней-не поспоришь! Мы решили проанализировать важность изучения производной в рамках школьной программы. И показать это в цифрах!Часть первая
Слайд 2Статистика-вещь серьезная. С ней-не поспоришь! Мы решили проанализировать важность изучения производной в рамках школьной
программы. И показать это в цифрах!
Часть первая
Слайд 3Математики о производной.
« Слова «производная» и «произошло»
имеют похожие части слова, да и смысл похож: производная происходит от исходной функции (переложив на отношения человека: исходная функция- «мама»,её производная «дочь»).Производная- часть математической науки, одно из её звеньев.Нет этого звена- прерваны связи между многими понятиями.»
Лукьянова Н.Н. учитель математики
Лукьянова Н.Н. учитель математики
Слайд 4Физики о производной.
« С производной в курсе
физики мы встречаемся в 10-11 классах.
В теме «Кинематика»: скорость- есть первая производная от перемещения.
В теме «Механические и электро- магнитные колебания» применяется производная от функции sinx и cosx.
Мой совет:
«Лучше изучайте математику, чтобы легче изучать другие науки.
Дерзайте!»
В теме «Кинематика»: скорость- есть первая производная от перемещения.
В теме «Механические и электро- магнитные колебания» применяется производная от функции sinx и cosx.
Мой совет:
«Лучше изучайте математику, чтобы легче изучать другие науки.
Дерзайте!»
Да, все учителя заодно! Что ж, посмотрим цифры. Они беспристрастны!
Слайд 6 Как часто в школьной программе используется производная
при решении различных математических задач? Мы перелистали и перечитали школьные учебники, экзаменационные сборники, тесты ЕГЭ, подборку материалов с вступительными экзаменами в институты за
последние несколько лет.
И что же получилось?
последние несколько лет.
И что же получилось?
Нам стало интересно…
Слайд 7Производная используется при решении следующих заданий:
Вычислить производную
Вычислить производную в заданной точке
Все задания на построение касательной к графику функции
Нахождение промежутков возрастания и убывания функции Нахождение точек экстремума
Нахождение скорости тела в момент времени
Нахождение наименьшего или наибольшего значения функции
Построение графиков с помощью производной
Исследование функции
Решение задач методом математического моделирования
Все задания на построение касательной к графику функции
Нахождение промежутков возрастания и убывания функции Нахождение точек экстремума
Нахождение скорости тела в момент времени
Нахождение наименьшего или наибольшего значения функции
Построение графиков с помощью производной
Исследование функции
Решение задач методом математического моделирования
Слайд 9Поступление в
ВУЗы
Изучив материалы вступительных экзаменов в
ВУЗы за многие прошедшие годы мы заметили, что в них встречаются только задания на нахождение наибольшего и наименьшего значения величины. Эти задачи отличаются повышенной сложностью, чтобы их решить нужно знать многие вопросы изучения производной в школе.
Слайд 10Вывод.
В школьной программе тема
«Производная и её
применение» является одной из важных, так как позволяет решать многие математические задачи более рациональным способом (например: исследование функции, нахождение точек максимума и минимума, решение задач на нахождение наибольшего или наименьшего значение величины).
Слайд 12Их, великих, загадочность окружающего мира притягивала, а исследование увлекало.
Честь открытия основных законов математического анализа принадлежит английскому физику и математику Исааку Ньютону и немецкому математику, физику, философу Лейбницу.
Слайд 13О великом Ньютоне!
Был этот мир глубокой тьмой окутан.
Да будет свет! И вот явился Ньютон. А.Поуг.
Исаак Ньютон (1643-1727) один из создателей дифференциального исчисления.
Главный его труд- «Математические начала натуральной философии».-оказал колоссальное влияние на развитие естествознания, стал поворотным пунктом в истории естествознания.
Ньютон ввёл понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.
Исаак Ньютон (1643-1727) один из создателей дифференциального исчисления.
Главный его труд- «Математические начала натуральной философии».-оказал колоссальное влияние на развитие естествознания, стал поворотным пунктом в истории естествознания.
Ньютон ввёл понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.
Слайд 14О Лейбнице.
«Предупреждаю, чтобы остерегались отбрасывать dx,-ошибка,
которую часто допускают и которая препятствует продвижению вперёд». Г.В.Лейбниц. (1646-1716)
Создатель Берлинской академии наук. Основоположник дифференци- ального исчисления, ввёл большую часть современной символики матема- тического анализа.
Лейбниц пришёл к понятию производной решая задачу проведения касательной к производной линии, объяснив этим ее геометрический смысл .
Создатель Берлинской академии наук. Основоположник дифференци- ального исчисления, ввёл большую часть современной символики матема- тического анализа.
Лейбниц пришёл к понятию производной решая задачу проведения касательной к производной линии, объяснив этим ее геометрический смысл .
Слайд 15Но это не говорит о том, …
…что
до них эти вопросы не изучались. Задолго до этого Архимед не только решил задачу на построение касательной к такой сложной кривой, как спираль, применяя при этом предельные переходы, но и сумел найти максимум функции.
Эпизодически понятие касательной встречалось в работах итальянского математика И.Тартальи.
В 17в. на основе учения Г.Галилея активно развилась кинематическая концепция производной.Понятие производной встречается уже у Р.Декарта, французского математика Роберваля, английского учёного Д.Грегори, в работах И.Барроу.
Но систематическое учение с выдвижением двух основных проблем математического анализа развито Ньютоном и Лейбницем.
Эпизодически понятие касательной встречалось в работах итальянского математика И.Тартальи.
В 17в. на основе учения Г.Галилея активно развилась кинематическая концепция производной.Понятие производной встречается уже у Р.Декарта, французского математика Роберваля, английского учёного Д.Грегори, в работах И.Барроу.
Но систематическое учение с выдвижением двух основных проблем математического анализа развито Ньютоном и Лейбницем.
Слайд 16Последователи учений Ньютона и Лейбница. В последующем развитии идеи анализа (а
они очень быстро завоевали популярность и нашли
многих последователей), следует в первую очередь назвать имена учеников Лейбница - братьев Бернулли.
А. Лопиталь (1661-1704)который учился у Бернулли,уже в 1696 году издал первый печатный курс дифференциального исчисления.
Ряд крупных результатов получил Лагранж, его работы сыграли важную роль в осмыслении основ анализа.
Слайд 17Вывод:
Ньютон и Лейбниц, решая практические задачи в механике и геометрии, пришли
к одному понятию- производная, показав тем самым, что дифференциальное исчисление- это есть окружающая действительность, переложенная на математический язык.
Слайд 19Исследуя функции, мы встретились со случаями, когда функция определена, но не
дифференцируема.
Мы задумались. Что это?
Почему так происходит?
Можно ли этому найти объяснения?
Вопросов было много и хотелось на них найти ответы.
Мы задумались. Что это?
Почему так происходит?
Можно ли этому найти объяснения?
Вопросов было много и хотелось на них найти ответы.
Слайд 20Взгляд из детства.
Всем с детства известно такое явление, как движение мяча,
падающего на пол и упруго отскакивающего от него.
Это явление можно объяснить с помощью законов физики.
Мы же попробовали переложить все это на математический язык.
Это явление можно объяснить с помощью законов физики.
Мы же попробовали переложить все это на математический язык.
Слайд 21При отскоке от пола (при h=0)направление движения мяча меняется (и функция
достигает минимума), однако в эти моменты скорость мяча не равна нулю, касательную к графику h провести нельзя.
На графике скорости мяча мы видим:в момент отскока скорость мяча однозначно найти нельзя- график скорости в эти моменты имеет разрывы.
(производная в этих точках не существует).
Слайд 23Примеры функций, имеющих особые точки. Все функции вида у=\f(x)\, при f(x)=0 имеют
особые точки- точки излома.
Частный случай: у=\х\
х=0- особая точка.
Слайд 24производная
При х=0 производная не существует (обращается в бесконечность), касательная становится вертикальной,
х=0 является особой точкой.
У функции
Слайд 26Наличие особых точек затрудняет исследования функции. Например: производная функции
у=\х\ там, где она определена, нигде не обращается в нуль, однако к функции нельзя применить необходимое условие экстремума и сказать, что она не имеет экстремумов. Х=0 является точкой минимума этой функции.
Слайд 27Вывод.
Окружающий мир очень сложен.И какие бы процессы мы не «заключали» в
рамки математических и физических законов, всегда найдутся исключения.
К ним нужно относиться очень внимательно и, главное, эти исключения из правил надо знать.
К ним нужно относиться очень внимательно и, главное, эти исключения из правил надо знать.