- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Внеклассное мероприятие на тему Математика - Царица наук
Содержание
- 1. Внеклассное мероприятие на тему Математика - Царица наук
- 2. РазминкаПодсчитать яблоки в корзинках У двух
- 3. Складывание кубиков На каждой грани бумажного
- 4. Треугольные участки На рисунке вы
- 5. Куб Если отпилить кубику одну вершину, на сколько измениться количество его вершин?Ответ: Увеличится на 6.
- 6. Площадь треугольника Все высоты треугольника меньше
- 7. Задача ЭйнштейнаА. Эйнштейн придумал эту задачу в
- 8. Задача ЭйнштейнаПодсказки:1.Англичанин живет в красном доме2.Швед держит
- 9. Задача ЭйнштейнаРешение:Ход решенияШАГ 1 По
- 10. Задача ЭйнштейнаШАГ 2 Из (9) следует,
- 11. Задача ЭйнштейнаШАГ 3 Зелёный дом не
- 12. Задача ЭйнштейнаШАГ 4 Где живёт
- 13. Шесть спичек Как из шести одинаковых
- 14. Получите три квадрата Переложите четыре спички
- 15. Печать Царя Соломона Сколько равносторонних треугольников
- 16. Конец
Слайд 2Разминка
Подсчитать яблоки в корзинках
У двух девочек есть по несколько
Сколько яблок у девочек?
Ответ: у первой 10, у второй 14
Ведро воды
Папе ведра воды хватает на две недели, а если вместе с сыном, то на 10 дней. Вопрос: на сколько дней хватит сыну ведра воды, если он будет пить один?
Сын пьет в 2.5 раз медленней, следовательно ему понадобится: 14 * 2.5 = 35 дней
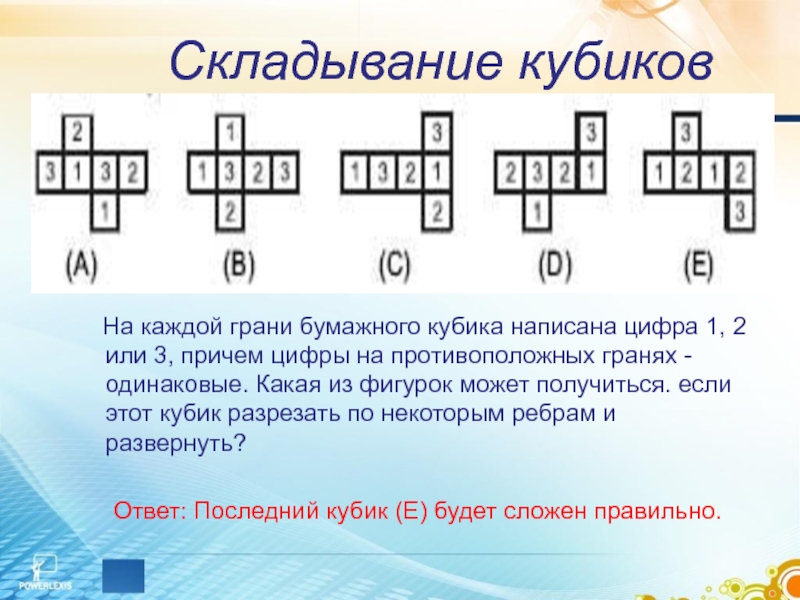
Слайд 3Складывание кубиков
На каждой грани бумажного кубика написана цифра 1,
Ответ: Последний кубик (Е) будет сложен правильно.
Слайд 4Треугольные участки
На рисунке вы видите, как шахтеры спорят
Катеты одного треугольника равны 140 и 48 , а его гипотенуза – 148. У второго треугольника катеты равны 80 и 84, а гипотенуза 116. Можете ли вы указать длины сторон третьего треугольника при условии, что они выражаются целыми числами, а площадь этого треугольника равняется площади первых двух треугольников?
Ответ: У третьего треугольника катеты равны 30 и 224, а гипотенуза – 226.
Слайд 5Куб
Если отпилить кубику одну вершину, на сколько измениться количество его
Ответ: Увеличится на 6.
Слайд 6Площадь треугольника
Все высоты треугольника меньше 1. Может ли его
Ответ: Может. Таким будет, например, равнобедренный треугольник, основание которого равно 80000, а высота к основанию равна 0.5.
Слайд 7Задача Эйнштейна
А. Эйнштейн придумал эту задачу в прошлом веке и полагал,
1. Есть 5 домов каждый разного цвета.
2. В каждом доме живет по одному человеку отличной друг от друга национальности.
3. Каждый жилец пьет только один определенный напиток, курит определенную марку сигарет и держит определенное животное.
4. Никто из 5 человек не пьет одинаковые с другими напитки, не курит одинаковые сигареты и не держит одинаковое животное.
Вопрос: кому принадлежит рыба?
Слайд 8Задача Эйнштейна
Подсказки:
1.Англичанин живет в красном доме
2.Швед держит собаку
3.Датчанин пьет чай
4.Зеленый дом
5.Жилец зеленого дома пьет кофе
6.Человек, который курит Pall Mall, держит птицу
7.Жилец из среднего дома пьет молоко
8.Жилец из желтого дома курит Dunhill
9.Норвежец живет в первом доме
10.Курильщик Marlboro живет около того, кто держит кошку
11.Человек, который содержит лошадь, живет около того, кто курит Dunhill
12.Курильщик сигарет Winfield пьет пиво
13.Норвежец живет около голубого дома
15.Немец курит Rothmans
16.Курильщик Marlboro живет по соседству с человеком, который пьет воду
Это всё, что необходимо для решения задачи.
Слайд 9Задача Эйнштейна
Решение:Ход решения
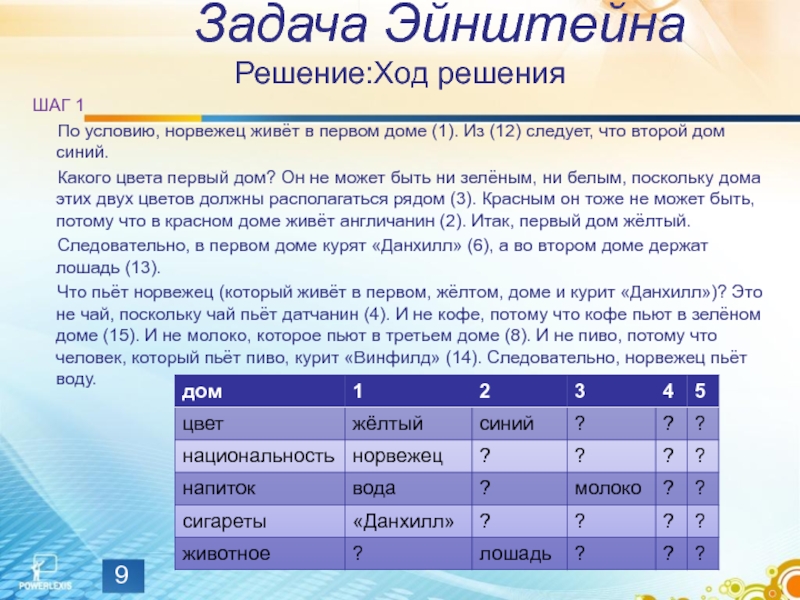
ШАГ 1
По условию, норвежец живёт в
Какого цвета первый дом? Он не может быть ни зелёным, ни белым, поскольку дома этих двух цветов должны располагаться рядом (3). Красным он тоже не может быть, потому что в красном доме живёт англичанин (2). Итак, первый дом жёлтый.
Следовательно, в первом доме курят «Данхилл» (6), а во втором доме держат лошадь (13).
Что пьёт норвежец (который живёт в первом, жёлтом, доме и курит «Данхилл»)? Это не чай, поскольку чай пьёт датчанин (4). И не кофе, потому что кофе пьют в зелёном доме (15). И не молоко, которое пьют в третьем доме (8). И не пиво, потому что человек, который пьёт пиво, курит «Винфилд» (14). Следовательно, норвежец пьёт воду.
Слайд 10Задача Эйнштейна
ШАГ 2
Из (9) следует, что человек, живущий во
Какой национальности человек, живущий во втором, синем, доме, предпочитающий «Мальборо» и держащий лошадь? Это не норвежец — он в первом доме (1). Не англичанин — он в красном доме (2). Не швед — у шведа собака (11). Не немец — немец курит «Ротманс» (7). Значит, во втором доме живёт датчанин и, как следует из (4), пьёт чай.
Слайд 11Задача Эйнштейна
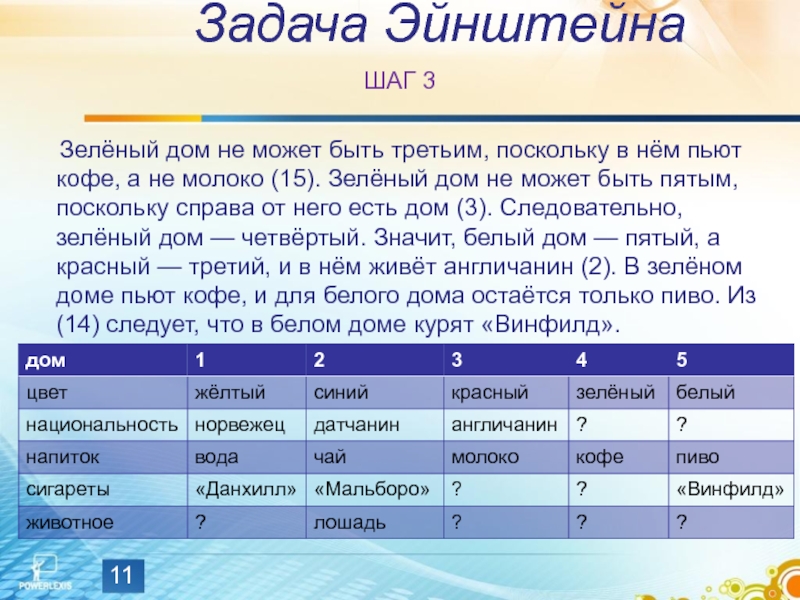
ШАГ 3
Зелёный дом не может быть третьим, поскольку
Слайд 12Задача Эйнштейна
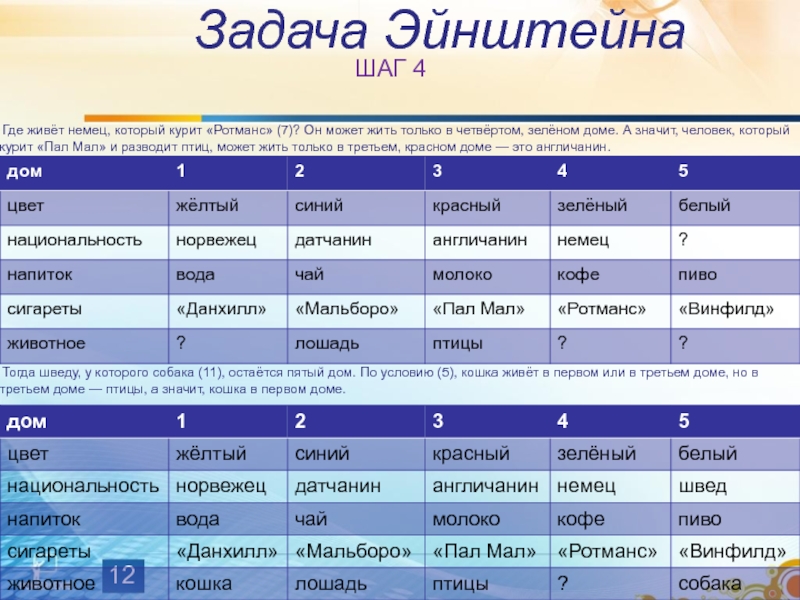
ШАГ 4
Где живёт немец, который курит «Ротманс»
Тогда шведу, у которого собака (11), остаётся пятый дом. По условию (5), кошка живёт в первом или в третьем доме, но в третьем доме — птицы, а значит, кошка в первом доме.
Слайд 13Шесть спичек
Как из шести одинаковых спичек сделать 4 равносторонних
Есть два решения, в одном случае стороны треугольников не равны длине спички, в другом - равны.
Ответ:
1. Спички пересекаются
2. Пирамида с равносторонним треугольником в основе
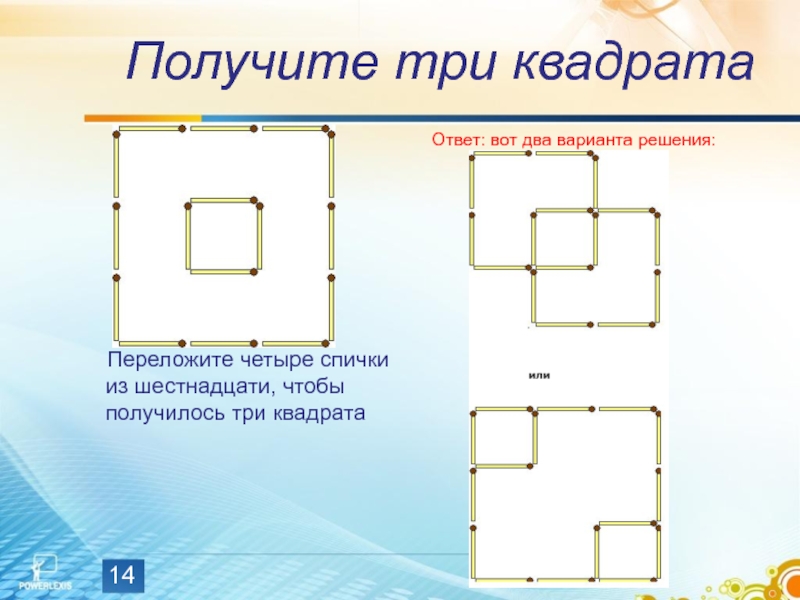
Слайд 14Получите три квадрата
Переложите четыре спички из шестнадцати, чтобы получилось
Ответ: вот два варианта решения:
Слайд 15Печать Царя Соломона
Сколько равносторонних треугольников изображено на знаменитой печати
Ответ: На печати Царя Соломона можно обнаружить 31 равносторонний треугольник.