- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок - презентация - Пропорция
Содержание
- 1. Урок - презентация - Пропорция
- 2. План урока:Что такое пропорция?Элементы пропорцииОсновное свойство пропорцииНахождение неизвестного члена пропорцииТестИсторические сведения
- 3. Что такое пропорция?Равенство двух отношений называют пропорциейнапример:или7,2: 1,2=3,6:0,6
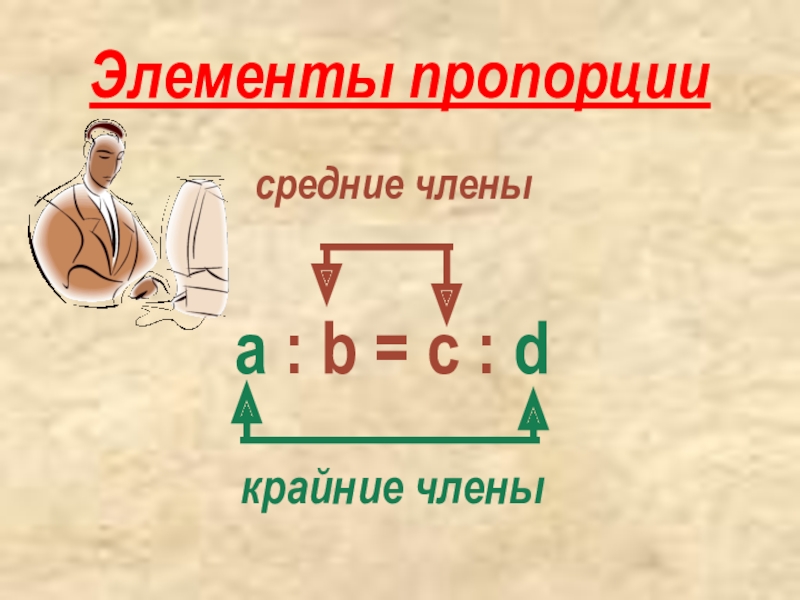
- 4. Элементы пропорции a : b = c : dсредние членыкрайние члены
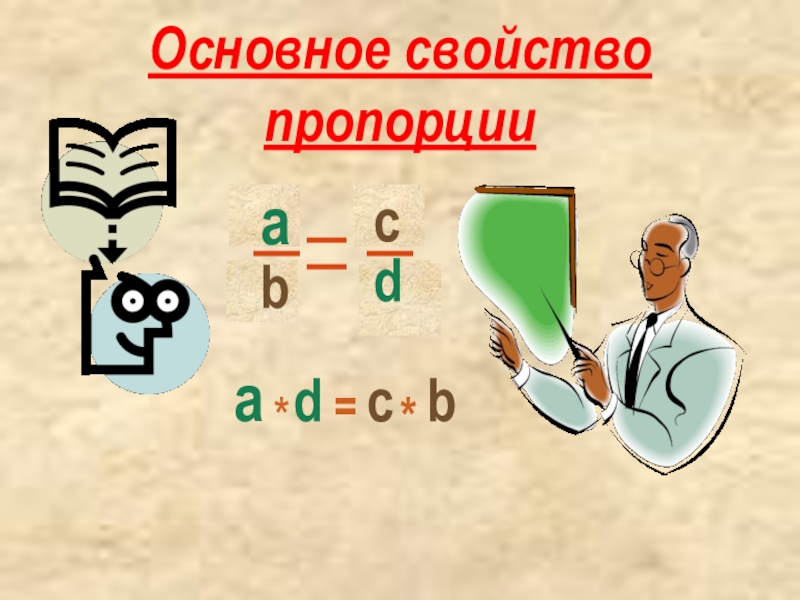
- 5. Основное свойство пропорции=
- 6. Нахождение неизвестного члена пропорциипример:решение:,значитили.
- 7. Нахождение неизвестного члена пропорциипример:решение:,значитили.
- 8. Нахождение неизвестного члена пропорции:Чтобы найти неизвестный средний
- 9. Тест1) равенство двух отношений называют
- 10. Тест1 вариант2 вариант3) в верной пропор-ции крайних
- 11. Тест1 вариант2 вариант5) неизвестный член в пропорции n:1,6=20:0,8равен .5) неизвестный член в пропорции2,7:3=с:10 равен .
- 12. Исторические сведенияГреческие учёные не призна-вали дробных чисел,
- 13. димых ими дворцов и храмов придавало этим
- 14. Пропорциональность в природе, искусстве, архитектуре означает соблюдение
- 15. Это отношение приближенно равно 0,618. Золотое сечение
Слайд 2План урока:
Что такое пропорция?
Элементы пропорции
Основное свойство пропорции
Нахождение неизвестного члена пропорции
Тест
Исторические сведения
Слайд 8Нахождение неизвестного члена пропорции:
Чтобы найти неизвестный средний член пропорции, нужно произведение
Чтобы найти неизвестный крайний член пропорции, нужно произведение средних членов разделить на известный крайний член пропорции
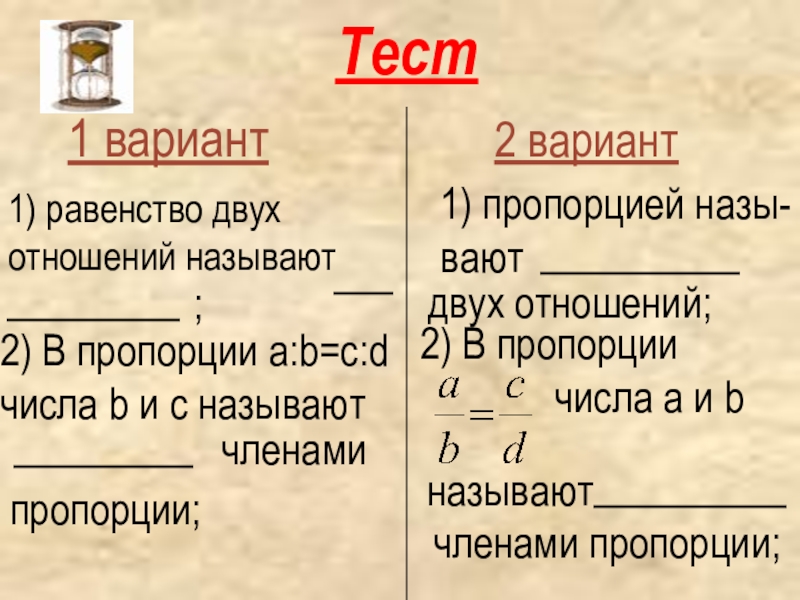
Слайд 9Тест
1) равенство двух
отношений называют
1) пропорцией назы-
вают
двух отношений;
1 вариант
2 вариант
2) В пропорции a:b=c:d
числа b и c называют
членами
пропорции;
2) В пропорции
числа a и b
называют
членами пропорции;
;
Слайд 10Тест
1 вариант
2 вариант
3) в верной пропор-
ции
крайних членов равно
средних;
3) если
крайних
сред-
них членов, то пропор-
ция
4) неизвестный сред-
ний член а в пропорции
28:а=7:5 равен
4) неизвестный край-
ний член m в пропор-
ции 36:4=90:m равен
;
;
;
Слайд 11Тест
1 вариант
2 вариант
5) неизвестный член в
пропорции n:1,6=20:0,8
равен
.
5) неизвестный член
в пропорции
2,7:3=с:10 равен
.
Слайд 12Исторические сведения
Греческие учёные не призна-
вали дробных чисел, у них
возникли затруднения с
мерением величин. Пришлось
греческим учёным придумывать
способ, как обходиться в науке без того, чтобы
выражать длины, площади и объёмы числами
(купцы и ремесленники спокойно делали это, не
обращая внимания на умствования учёных).
С пропорциями имели дело уже древние строи-
тели. Правильное соотношение размеров возво-
Слайд 13димых ими дворцов и храмов придавало этим зда-
ниям ту необыкновенную красоту,
восхищает нас.
Учение об отношениях и
пропорциях особенно успешно
развивалось в 4 в. до н. э. в
Древней Греции, славившейся
произведениями искусства, архитектуры. С пропор-
циями связывались представления о красоте, по-
рядке и гармонии, о созвучных аккордах в музыке.
Слайд 14Пропорциональность в природе, искусстве, архитектуре означает соблюдение определённых
соотношений между размерами отдельных
ного и красивого изображения.
Золотым сечением и даже «боже
ственной пропор-
цией» называли математики древности и средневе-
ковья деление отрезка, при котором длина всего
отрезка так относится к длине его большей части,
как длина большей части к меньшей.
Слайд 15Это отношение приближенно равно 0,618. Золотое
сечение чаще всего применяется в
искусства, архитектуре, встречается в природе.
Древние египетские пирамиды построены в пропор-
ции золотого сечения. Окружающие нас предметы
также дают примеры золотого сечения. Например,
переплёты многих книг имеют отношение длины и
ширины, близкое к числу 0,618.
Теперь роль пропорций стала меньше, но и до сих
пор их применяют в самых различных вопросах.