- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение геометрических задач по готовым чертежам
Содержание
- 1. Решение геометрических задач по готовым чертежам
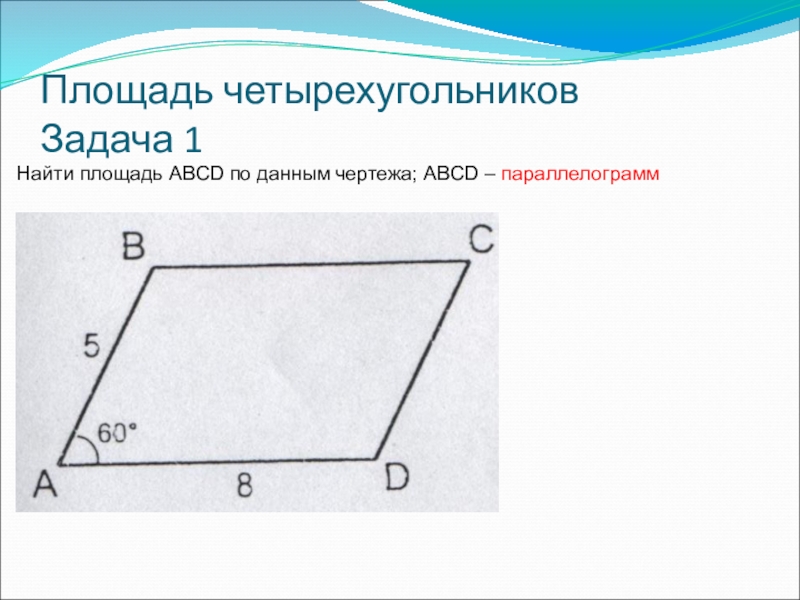
- 2. Площадь четырехугольников Задача 1Найти площадь ABCD по данным чертежа; ABCD – параллелограмм
- 3. Площадь четырехугольников Задача 1Найти площадь ABCD по
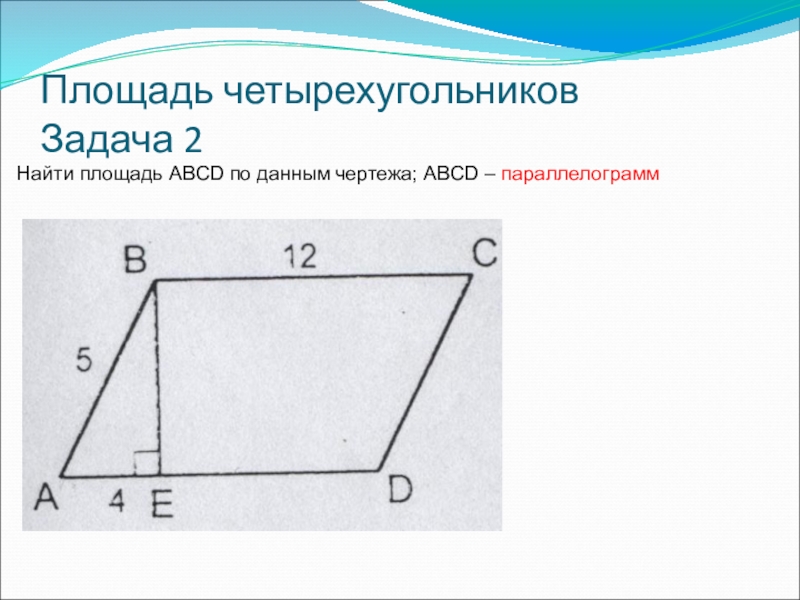
- 4. Площадь четырехугольников Задача 2Найти площадь ABCD по данным чертежа; ABCD – параллелограмм
- 5. Площадь четырехугольников Задача 2Найти площадь ABCD по данным чертежа; ABCD – параллелограмм∆BAE: угол E=90°По теореме ПифагораAB2=AE2+BE2S=BE•AD=12•3=36
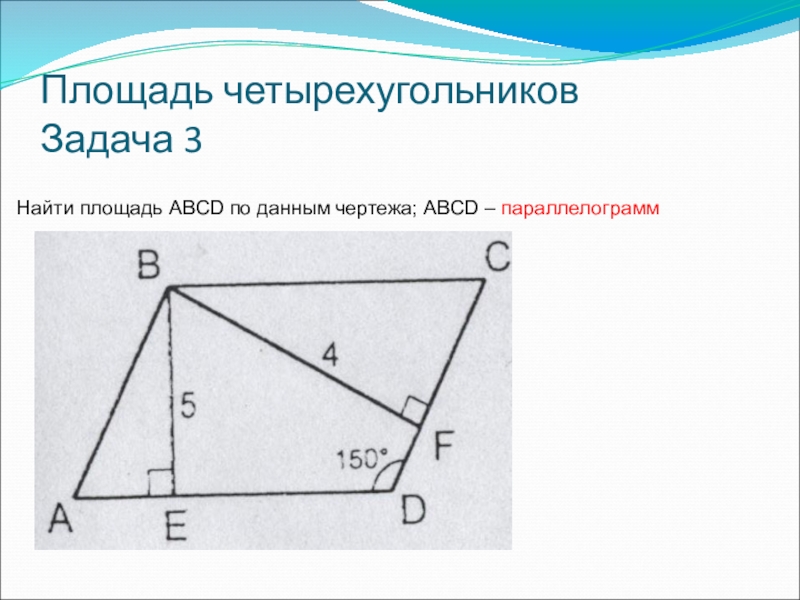
- 6. Площадь четырехугольников Задача 3Найти площадь ABCD по данным чертежа; ABCD – параллелограмм
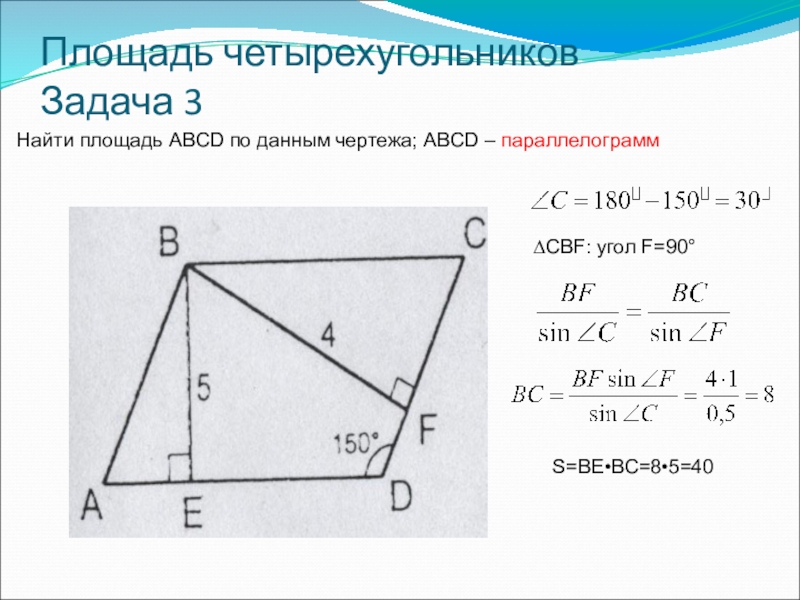
- 7. Площадь четырехугольников Задача 3Найти площадь ABCD по данным чертежа; ABCD – параллелограмм∆CBF: угол F=90°S=BE•BC=8•5=40
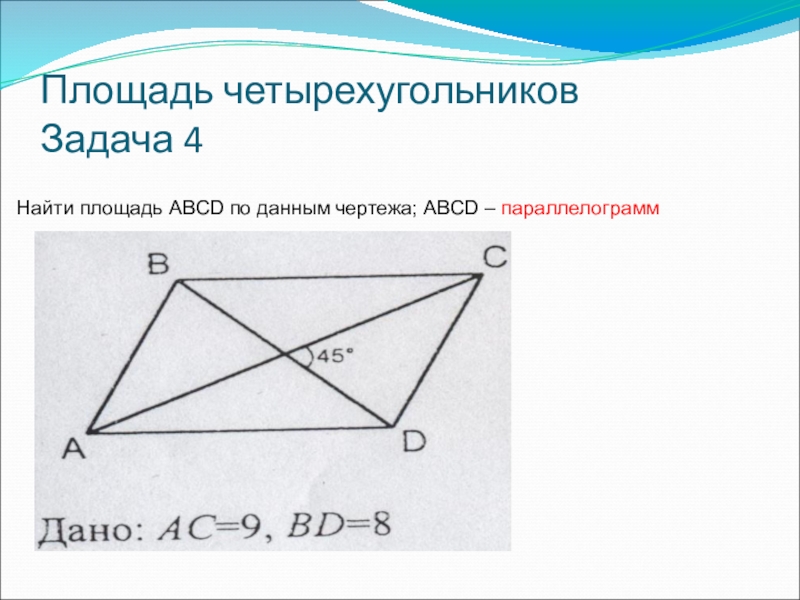
- 8. Площадь четырехугольников Задача 4Найти площадь ABCD по данным чертежа; ABCD – параллелограмм
- 9. Площадь четырехугольников Задача 4Найти площадь ABCD по данным чертежа; ABCD – параллелограмм
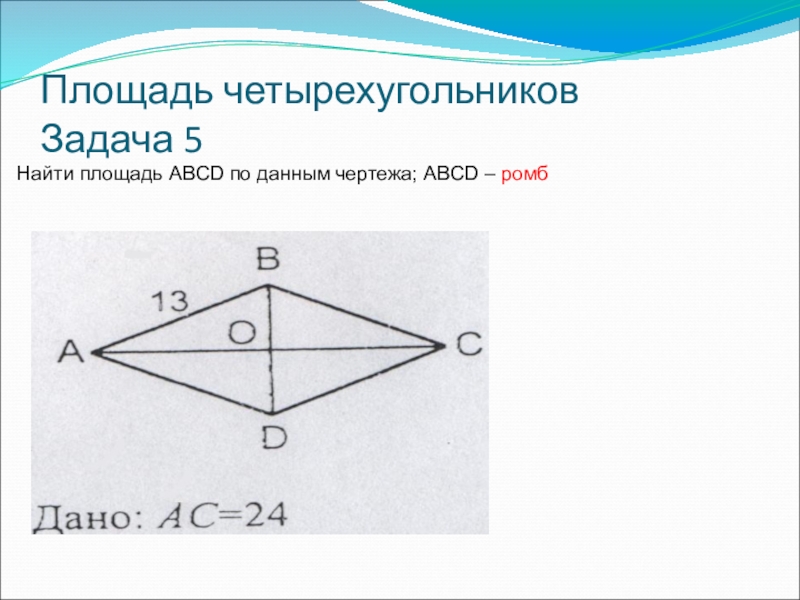
- 10. Площадь четырехугольников Задача 5Найти площадь ABCD по данным чертежа; ABCD – ромб
- 11. Площадь четырехугольников Задача 5Найти площадь ABCD по данным чертежа; ABCD – ромбBD=2BO=5•2=10∆AOB: угол O=90°
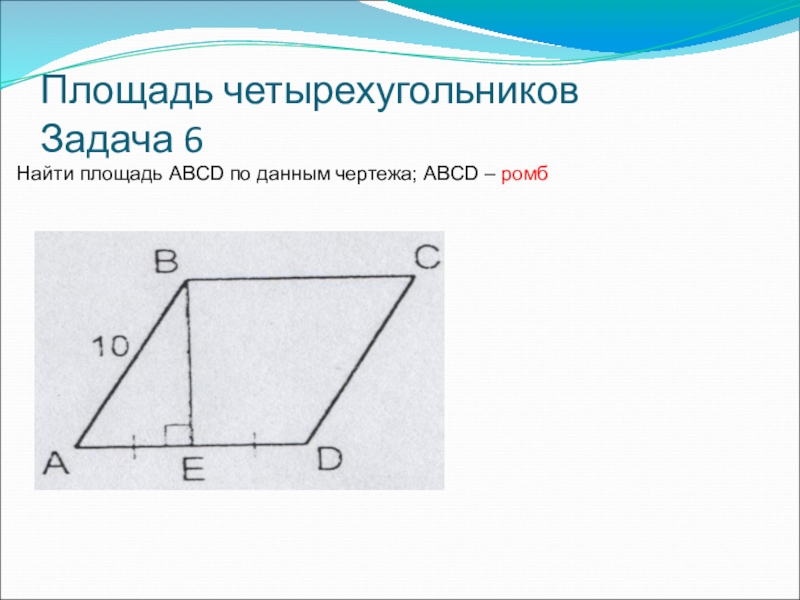
- 12. Площадь четырехугольников Задача 6Найти площадь ABCD по данным чертежа; ABCD – ромб
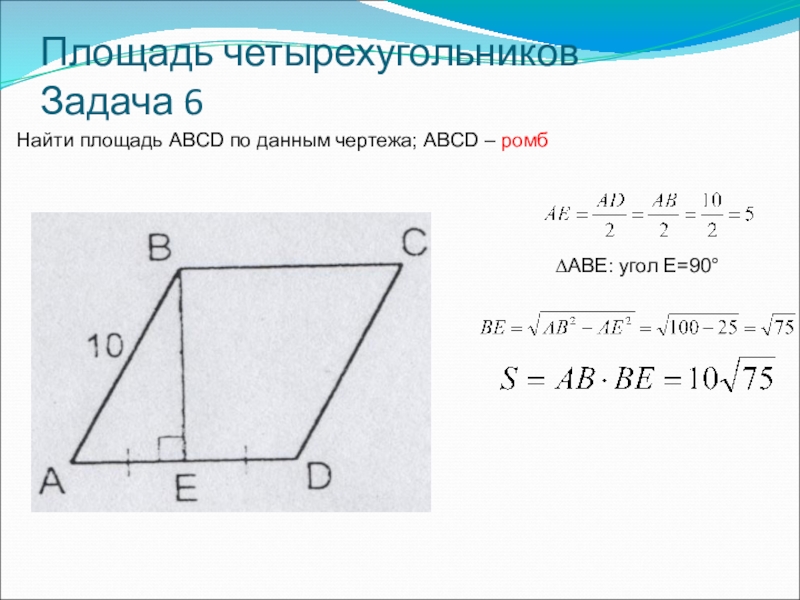
- 13. Площадь четырехугольников Задача 6Найти площадь ABCD по данным чертежа; ABCD – ромб∆ABE: угол E=90°
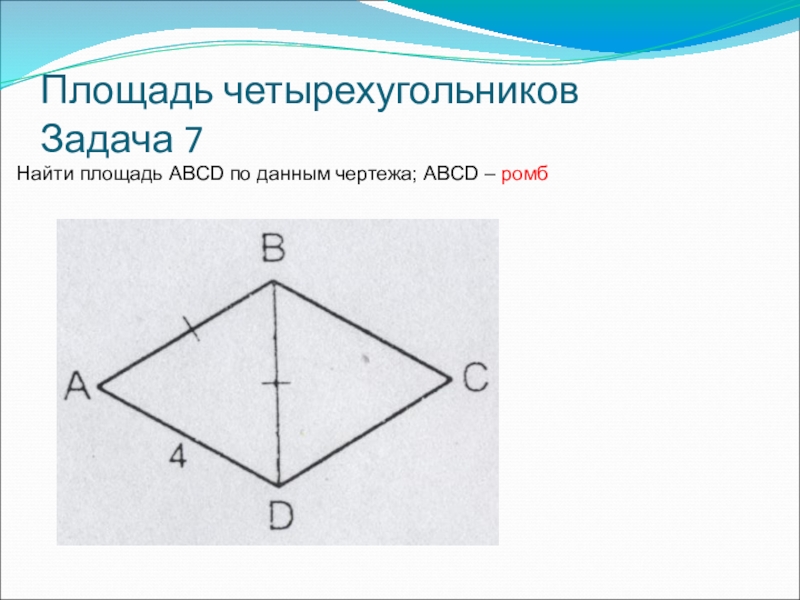
- 14. Площадь четырехугольников Задача 7Найти площадь ABCD по данным чертежа; ABCD – ромб
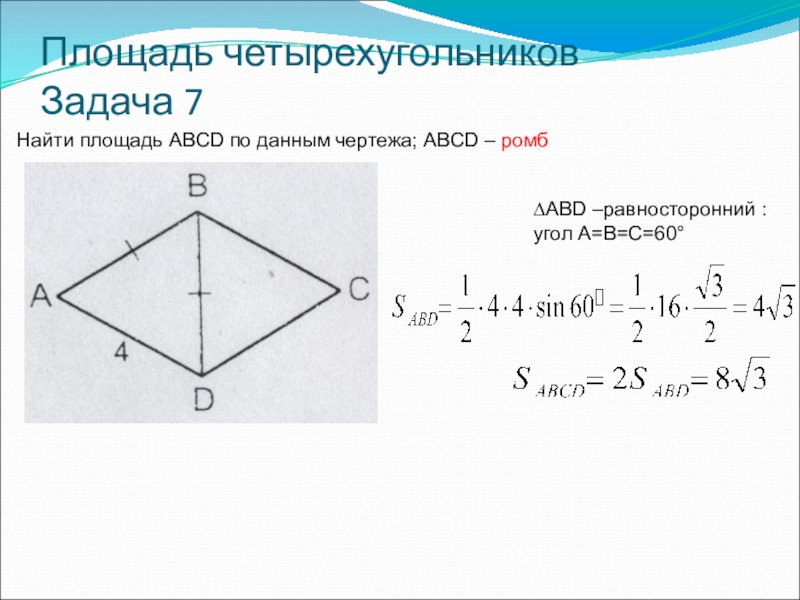
- 15. Площадь четырехугольников Задача 7Найти площадь ABCD по данным чертежа; ABCD – ромб∆ABD –равносторонний : угол A=B=C=60°
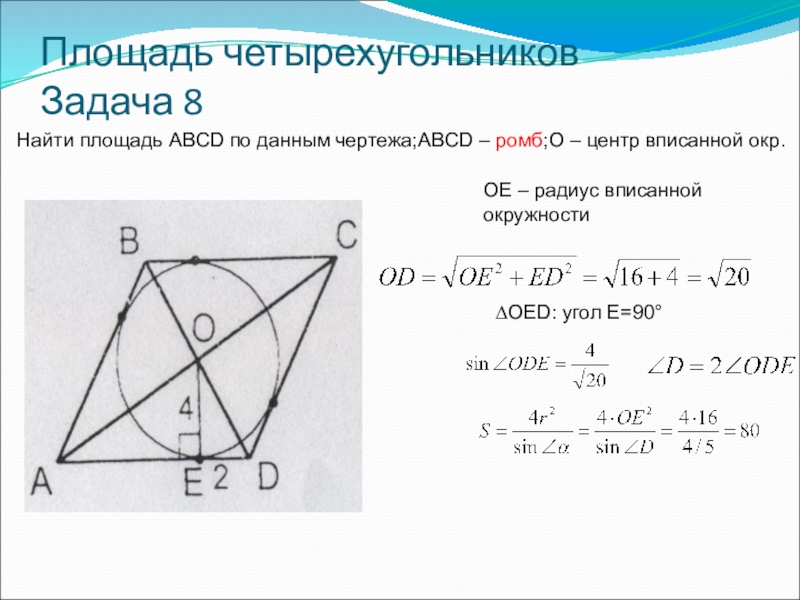
- 16. Площадь четырехугольников Задача 8Найти площадь ABCD по данным чертежа;ABCD – ромб;O – центр вписанной окружности.
- 17. Площадь четырехугольников Задача 8Найти площадь ABCD по
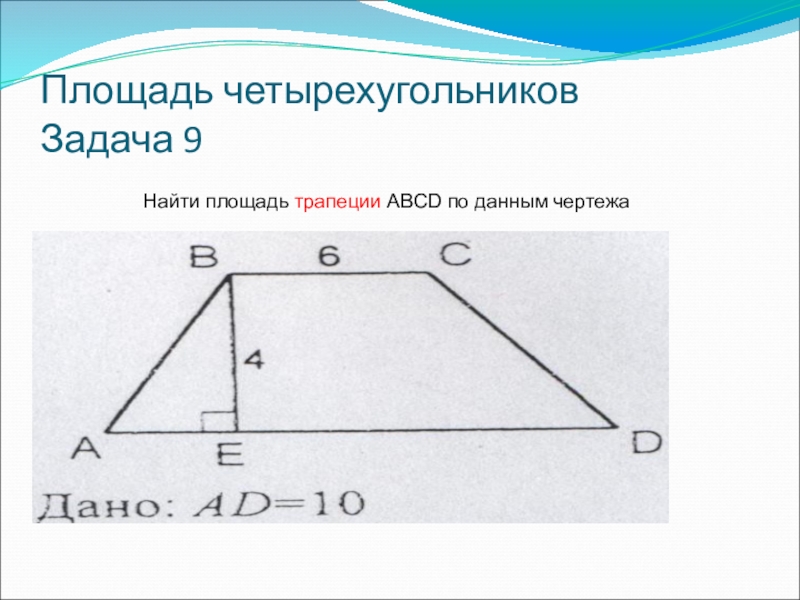
- 18. Площадь четырехугольников Задача 9Найти площадь трапеции ABCD по данным чертежа
- 19. Площадь четырехугольников Задача 9Найти площадь трапеции ABCD по данным чертежа
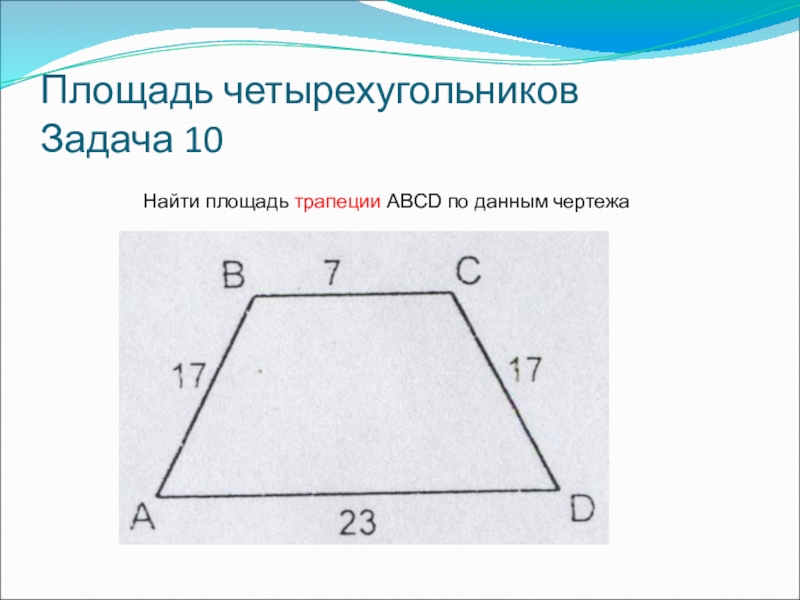
- 20. Площадь четырехугольников Задача 10Найти площадь трапеции ABCD по данным чертежа
- 21. Площадь четырехугольников Задача 10Найти площадь трапеции ABCD
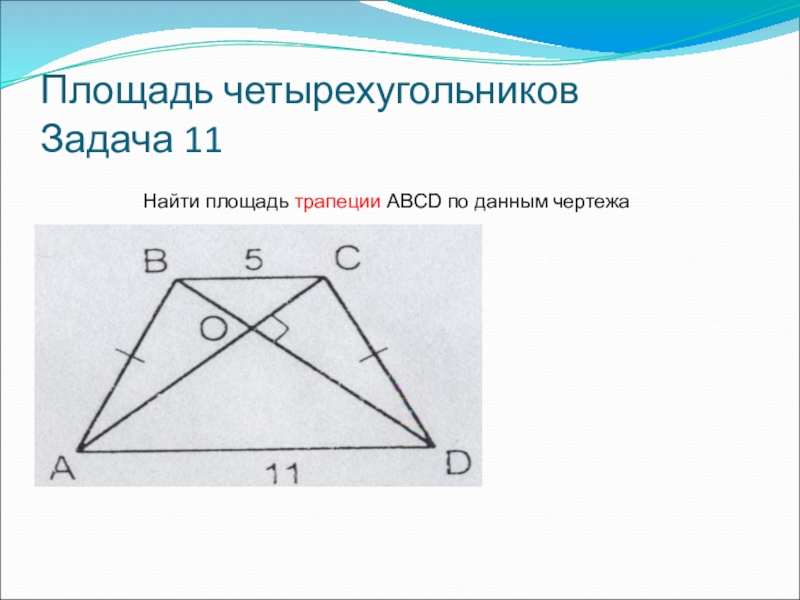
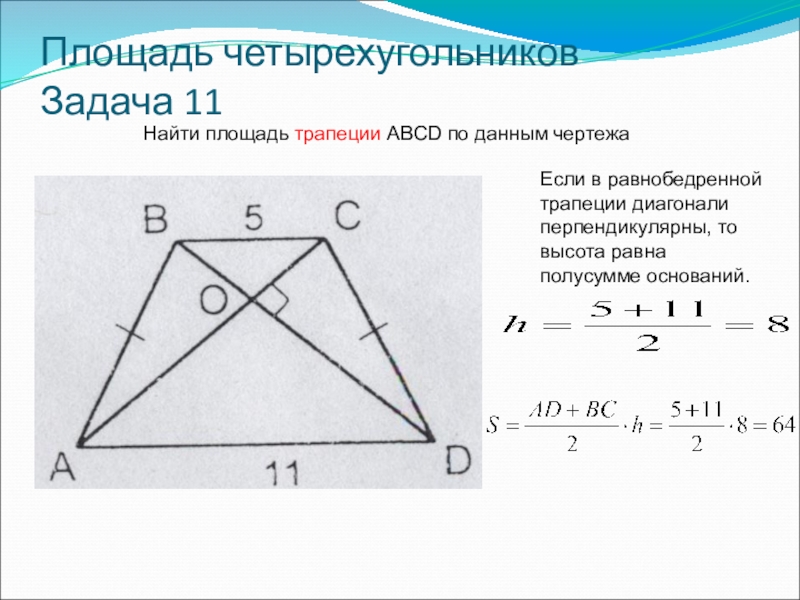
- 22. Площадь четырехугольников Задача 11Найти площадь трапеции ABCD по данным чертежа
- 23. Площадь четырехугольников Задача 11Найти площадь трапеции ABCD
- 24. Площадь четырехугольников Задача 12Найти площадь трапеции ABCD по данным чертежа;O – центр вписанной окружности.
- 25. Площадь четырехугольников Задача 12Найти площадь трапеции ABCD
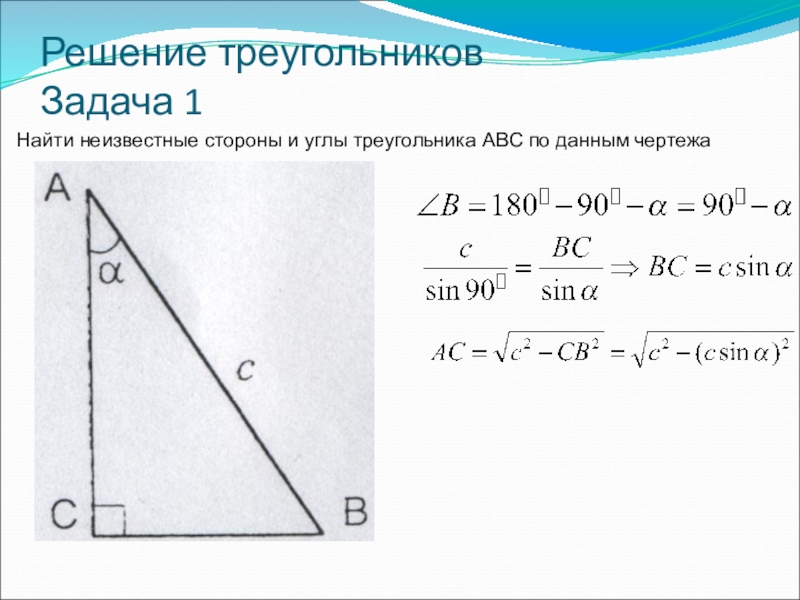
- 26. Решение треугольников Задача 1Найти неизвестные стороны и углы треугольника ABC по данным чертежа
- 27. Решение треугольников Задача 1Найти неизвестные стороны и углы треугольника ABC по данным чертежа
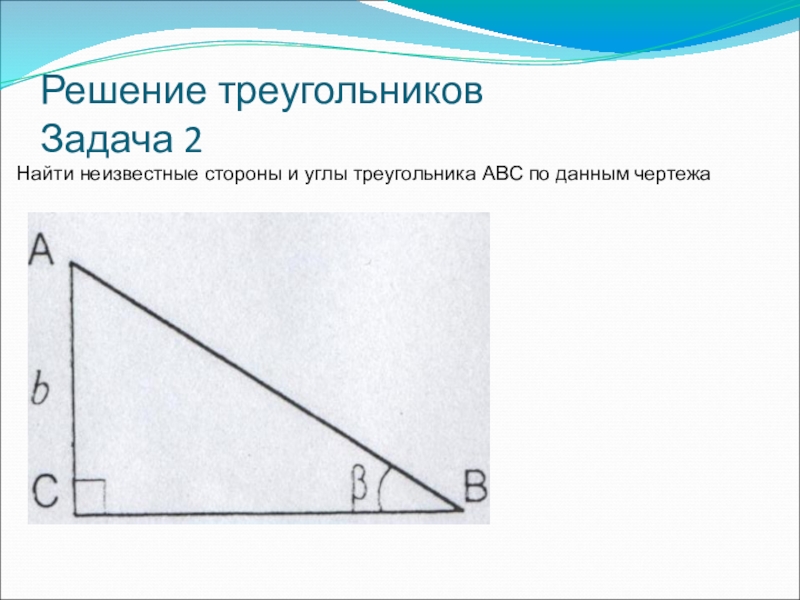
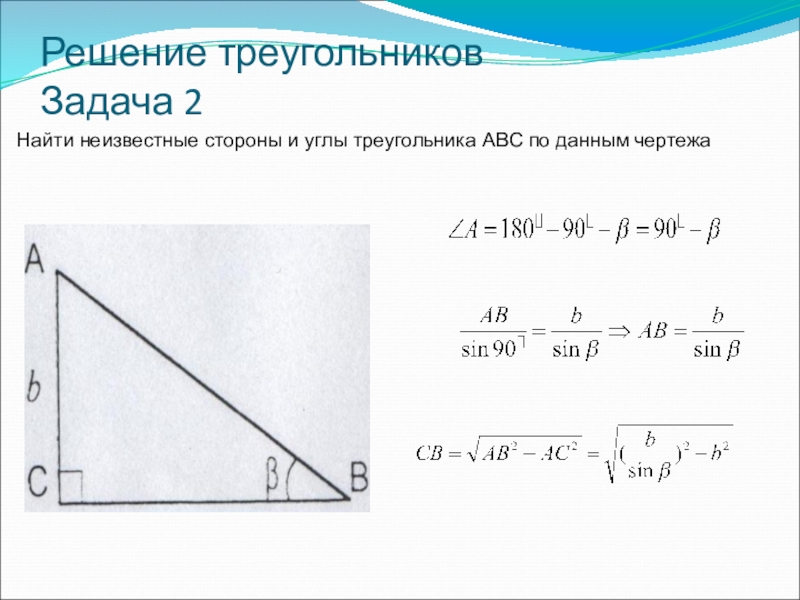
- 28. Решение треугольников Задача 2Найти неизвестные стороны и углы треугольника ABC по данным чертежа
- 29. Решение треугольников Задача 2Найти неизвестные стороны и углы треугольника ABC по данным чертежа
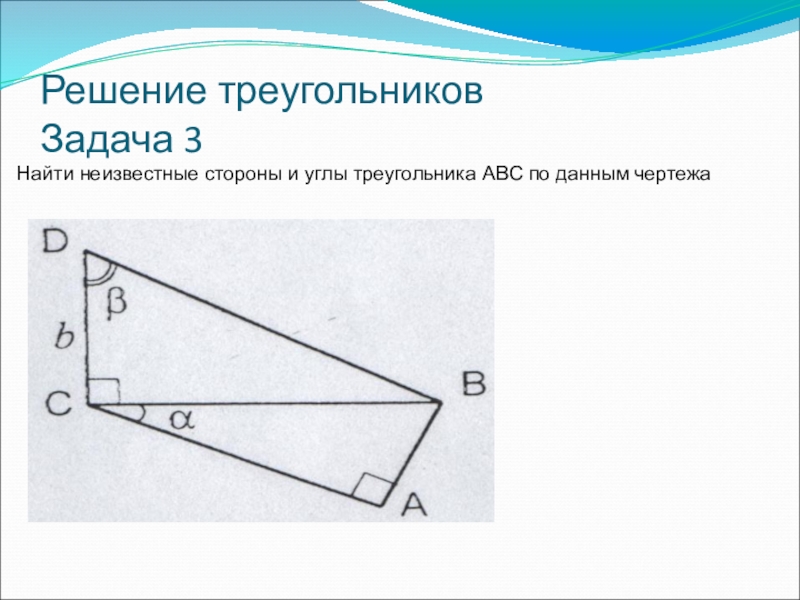
- 30. Решение треугольников Задача 3Найти неизвестные стороны и углы треугольника ABC по данным чертежа
- 31. Решение треугольников Задача 3Найти неизвестные стороны и углы треугольника ABC по данным чертежа
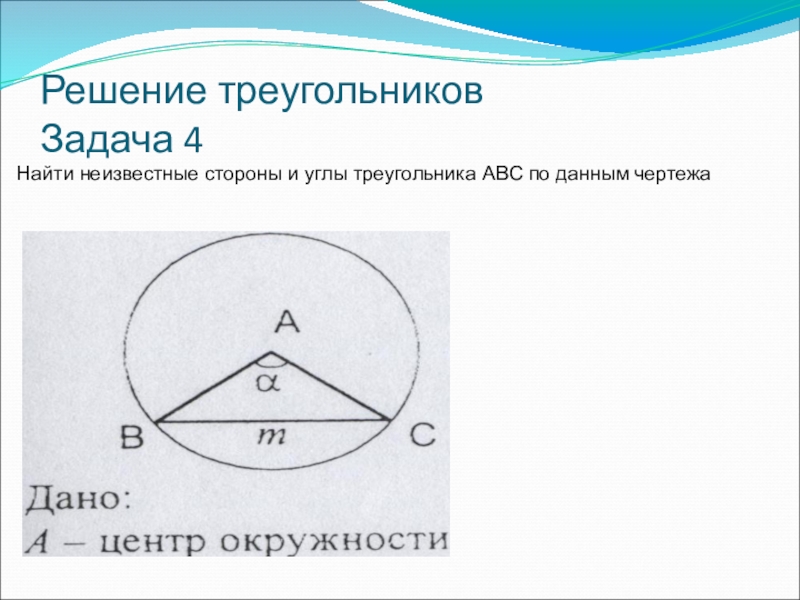
- 32. Решение треугольников Задача 4Найти неизвестные стороны и углы треугольника ABC по данным чертежа
- 33. Решение треугольников Задача 4Найти неизвестные стороны и углы треугольника ABC по данным чертежаAB=AC=R →∆ABC-равнобедренный
- 34. Решение треугольников Задача 5Найти неизвестные стороны и углы треугольника ABC по данным чертежа
- 35. Решение треугольников Задача 5Найти неизвестные стороны и углы треугольника ABC по данным чертежа
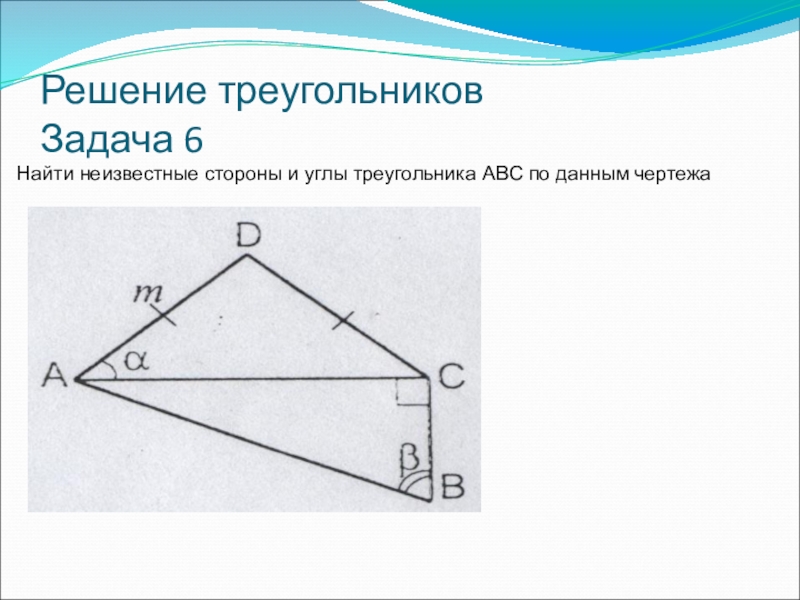
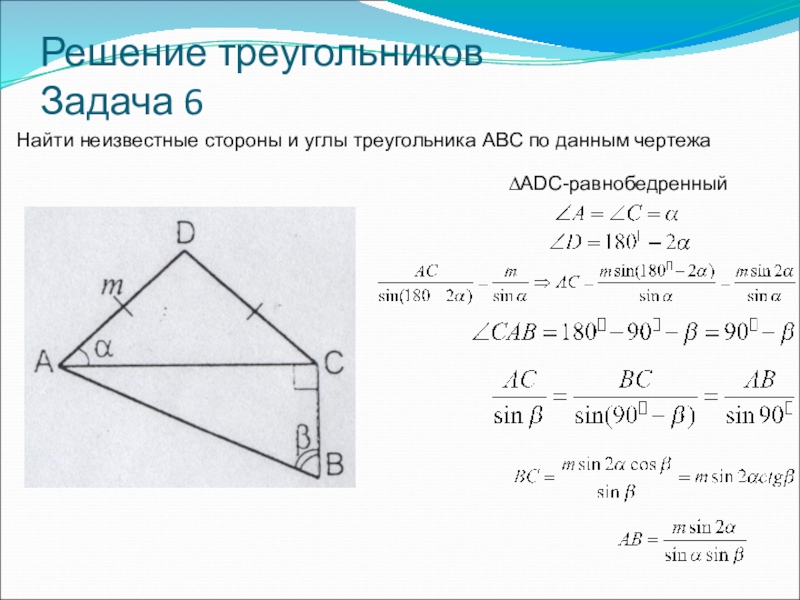
- 36. Решение треугольников Задача 6Найти неизвестные стороны и углы треугольника ABC по данным чертежа
- 37. Решение треугольников Задача 6Найти неизвестные стороны и углы треугольника ABC по данным чертежа∆ADC-равнобедренный
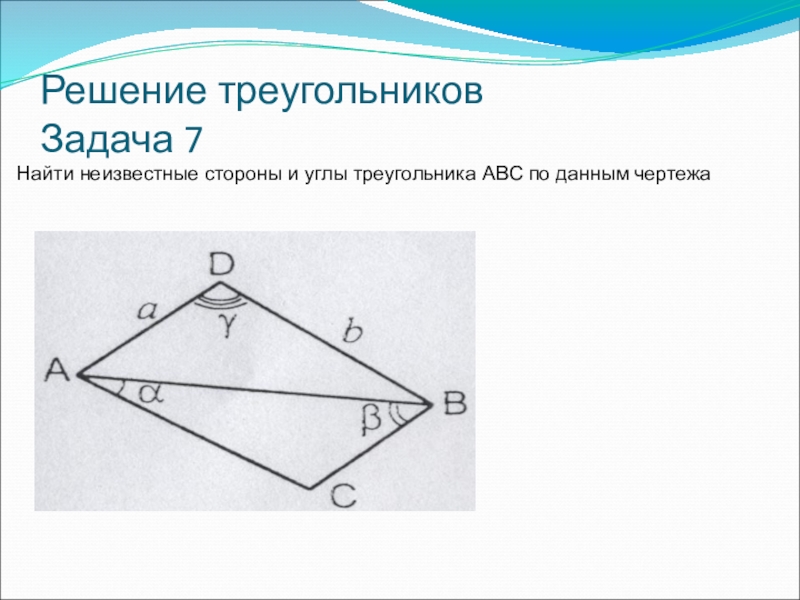
- 38. Решение треугольников Задача 7Найти неизвестные стороны и углы треугольника ABC по данным чертежа
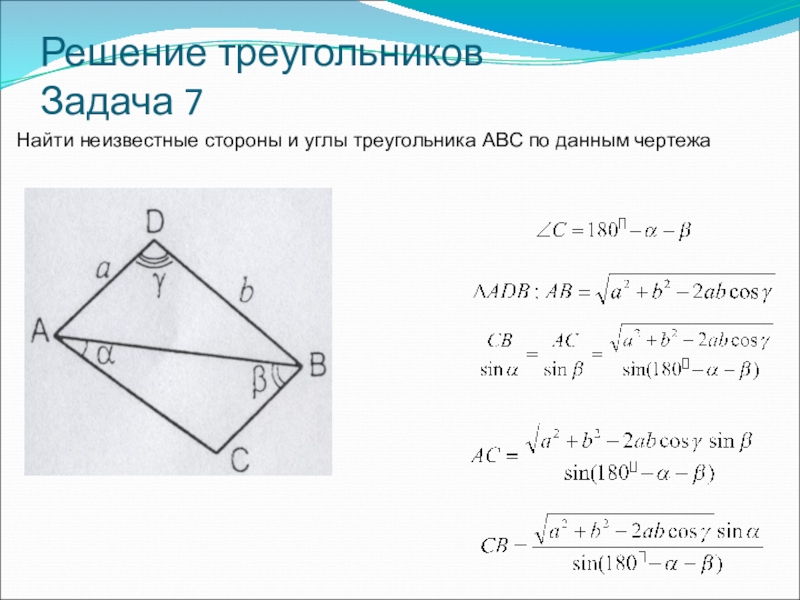
- 39. Решение треугольников Задача 7Найти неизвестные стороны и углы треугольника ABC по данным чертежа
- 40. Решение треугольников Задача 8Найти неизвестные стороны и углы треугольника ABC по данным чертежа
- 41. Решение треугольников Задача 8Найти неизвестные стороны и углы треугольника ABC по данным чертежа∆ABC-равнобедренный∆DOC: OD=r
- 42. Решение треугольников Задача 9Найти неизвестные стороны и углы треугольника ABC по данным чертежа
- 43. Решение треугольников Задача 9Найти неизвестные стороны и углы треугольника ABC по данным чертежа
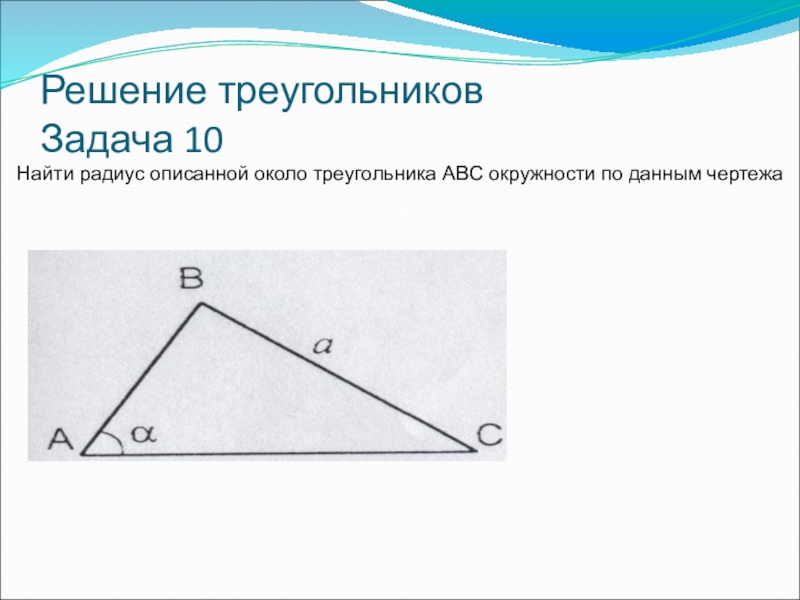
- 44. Решение треугольников Задача 10Найти радиус описанной около треугольника ABC окружности по данным чертежа
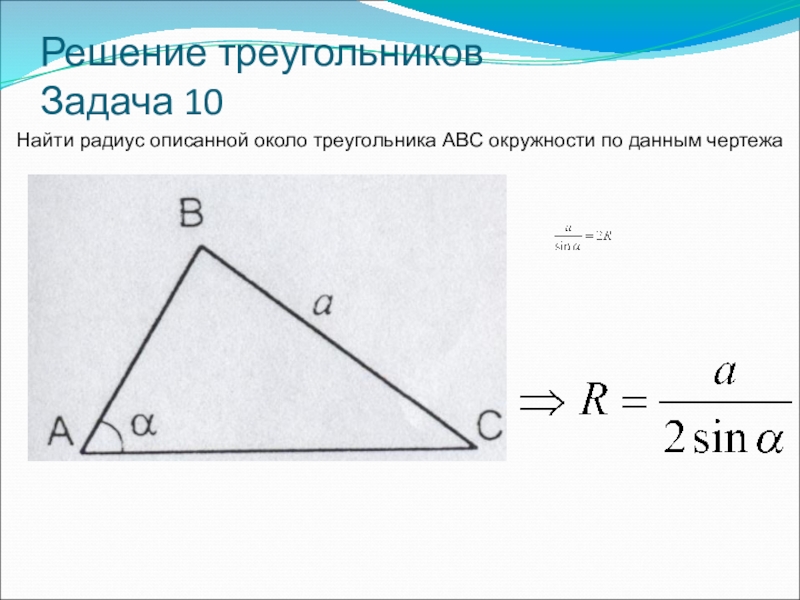
- 45. Решение треугольников Задача 10Найти радиус описанной около треугольника ABC окружности по данным чертежа
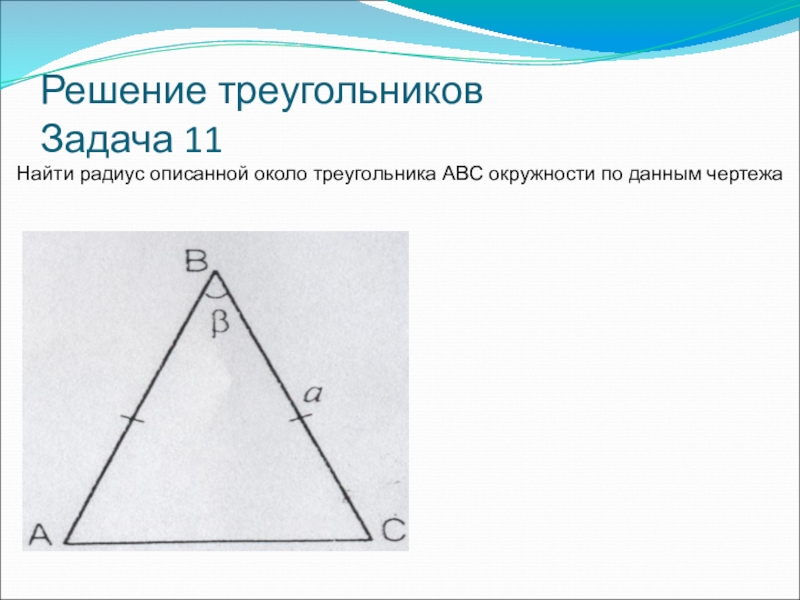
- 46. Решение треугольников Задача 11Найти радиус описанной около треугольника ABC окружности по данным чертежа
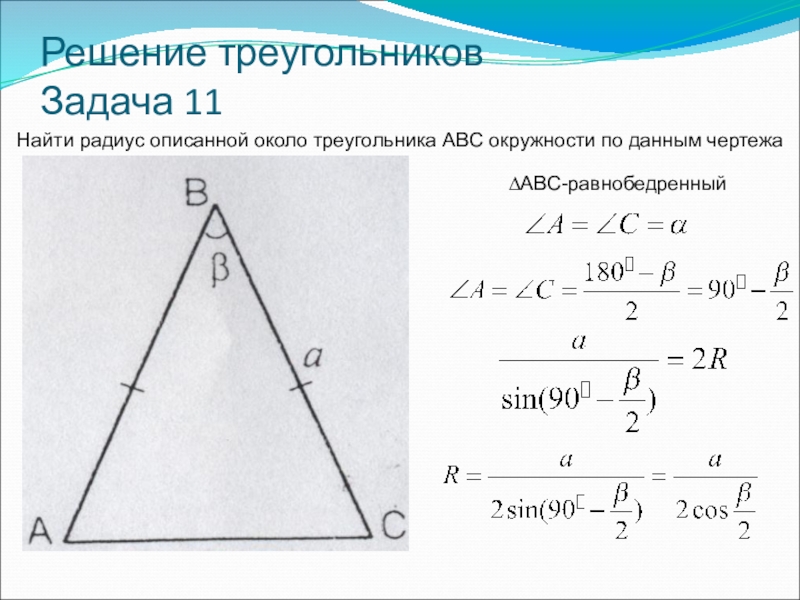
- 47. Решение треугольников Задача 11Найти радиус описанной около треугольника ABC окружности по данным чертежа∆ABC-равнобедренный
- 48. Решение треугольников Задача 12Найти радиус описанной около треугольника ABC окружности по данным чертежа
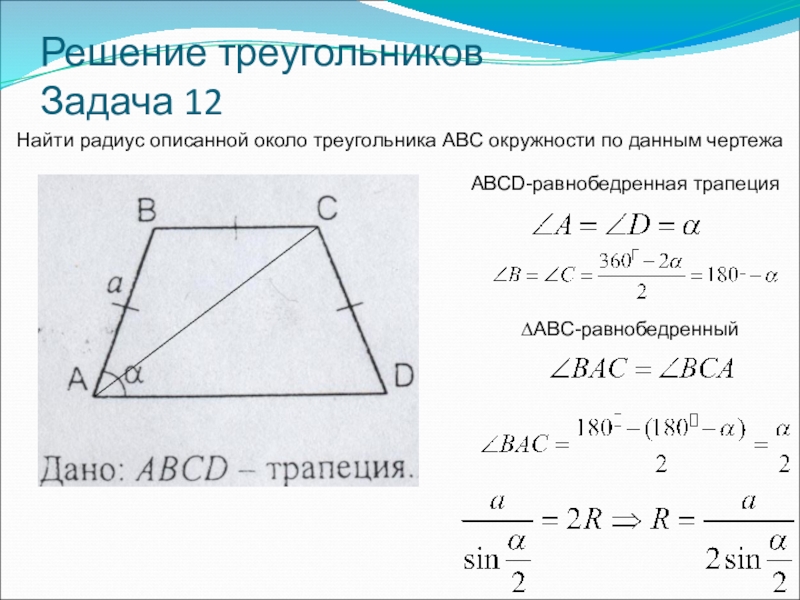
- 49. Решение треугольников Задача 12Найти радиус описанной около треугольника ABC окружности по данным чертежаABCD-равнобедренная трапеция
- 50. Решение треугольников Задача 12Найти радиус описанной около треугольника ABC окружности по данным чертежа∆ABC-равнобедренныйABCD-равнобедренная трапеция
Слайд 1Решение задач по готовым чертежам
Площадь четырехугольника
Решение треугольников
9-10 класс
МБОУ Гимназия№4
г. Новосибирска
Баринова Людмила Леонидовна учитель высшей квалификационной категории
Слайд 2Площадь четырехугольников
Задача 1
Найти площадь ABCD по данным чертежа; ABCD – параллелограмм
Слайд 3Площадь четырехугольников
Задача 1
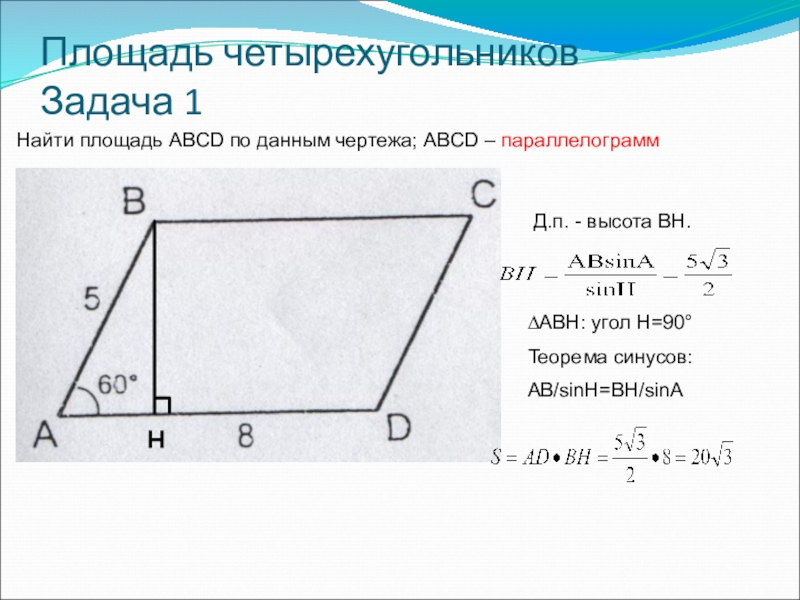
Найти площадь ABCD по данным чертежа; ABCD – параллелограмм
Д.п.
∆ABH: угол H=90°
Теорема синусов:
AB/sinH=BH/sinA
Слайд 4Площадь четырехугольников
Задача 2
Найти площадь ABCD по данным чертежа; ABCD – параллелограмм
Слайд 5Площадь четырехугольников
Задача 2
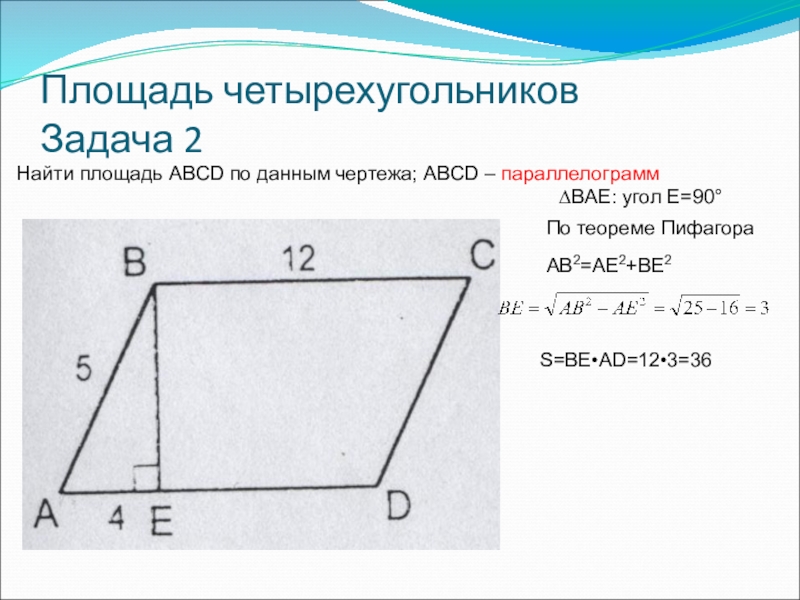
Найти площадь ABCD по данным чертежа; ABCD – параллелограмм
∆BAE:
По теореме Пифагора
AB2=AE2+BE2
S=BE•AD=12•3=36
Слайд 6Площадь четырехугольников
Задача 3
Найти площадь ABCD по данным чертежа; ABCD – параллелограмм
Слайд 7Площадь четырехугольников
Задача 3
Найти площадь ABCD по данным чертежа; ABCD – параллелограмм
∆CBF:
S=BE•BC=8•5=40
Слайд 8Площадь четырехугольников
Задача 4
Найти площадь ABCD по данным чертежа; ABCD – параллелограмм
Слайд 9Площадь четырехугольников
Задача 4
Найти площадь ABCD по данным чертежа; ABCD – параллелограмм
Слайд 11Площадь четырехугольников
Задача 5
Найти площадь ABCD по данным чертежа; ABCD – ромб
BD=2BO=5•2=10
∆AOB:
Слайд 13Площадь четырехугольников
Задача 6
Найти площадь ABCD по данным чертежа; ABCD – ромб
∆ABE:
Слайд 15Площадь четырехугольников
Задача 7
Найти площадь ABCD по данным чертежа; ABCD – ромб
∆ABD
Слайд 16Площадь четырехугольников
Задача 8
Найти площадь ABCD по данным чертежа;ABCD – ромб;O –
Слайд 17Площадь четырехугольников
Задача 8
Найти площадь ABCD по данным чертежа;ABCD – ромб;O –
OE – радиус вписанной окружности
∆OED: угол E=90°
Слайд 21Площадь четырехугольников
Задача 10
Найти площадь трапеции ABCD по данным чертежа
Д.п. - высоты
HH1=BC=7
∆ABH: угол H=90°
Слайд 23Площадь четырехугольников
Задача 11
Найти площадь трапеции ABCD по данным чертежа
Если в равнобедренной
Слайд 24Площадь четырехугольников
Задача 12
Найти площадь трапеции ABCD по данным чертежа;O – центр
Слайд 25Площадь четырехугольников
Задача 12
Найти площадь трапеции ABCD по данным чертежа;O – центр
Если в трапецию вписана окружность радиуса r, и она делит боковую сторону точкой касания на два отрезка a и b, то справедливо следующее равенство:
BC=4+6=10 AD=9+6=15(свойство отрезков касательных)
CD=2r=6•2=12
Слайд 26Решение треугольников
Задача 1
Найти неизвестные стороны и углы треугольника ABC по данным
Слайд 27Решение треугольников
Задача 1
Найти неизвестные стороны и углы треугольника ABC по данным
Слайд 28Решение треугольников
Задача 2
Найти неизвестные стороны и углы треугольника ABC по данным
Слайд 29Решение треугольников
Задача 2
Найти неизвестные стороны и углы треугольника ABC по данным
Слайд 30Решение треугольников
Задача 3
Найти неизвестные стороны и углы треугольника ABC по данным
Слайд 31Решение треугольников
Задача 3
Найти неизвестные стороны и углы треугольника ABC по данным
Слайд 32Решение треугольников
Задача 4
Найти неизвестные стороны и углы треугольника ABC по данным
Слайд 33Решение треугольников
Задача 4
Найти неизвестные стороны и углы треугольника ABC по данным
AB=AC=R →∆ABC-равнобедренный
Слайд 34Решение треугольников
Задача 5
Найти неизвестные стороны и углы треугольника ABC по данным
Слайд 35Решение треугольников
Задача 5
Найти неизвестные стороны и углы треугольника ABC по данным
Слайд 36Решение треугольников
Задача 6
Найти неизвестные стороны и углы треугольника ABC по данным
Слайд 37Решение треугольников
Задача 6
Найти неизвестные стороны и углы треугольника ABC по данным
∆ADC-равнобедренный
Слайд 38Решение треугольников
Задача 7
Найти неизвестные стороны и углы треугольника ABC по данным
Слайд 39Решение треугольников
Задача 7
Найти неизвестные стороны и углы треугольника ABC по данным
Слайд 40Решение треугольников
Задача 8
Найти неизвестные стороны и углы треугольника ABC по данным
Слайд 41Решение треугольников
Задача 8
Найти неизвестные стороны и углы треугольника ABC по данным
∆ABC-равнобедренный
∆DOC: OD=r
Слайд 42Решение треугольников
Задача 9
Найти неизвестные стороны и углы треугольника ABC по данным
Слайд 43Решение треугольников
Задача 9
Найти неизвестные стороны и углы треугольника ABC по данным
Слайд 44Решение треугольников
Задача 10
Найти радиус описанной около треугольника ABC окружности по данным
Слайд 45Решение треугольников
Задача 10
Найти радиус описанной около треугольника ABC окружности по данным
Слайд 46Решение треугольников
Задача 11
Найти радиус описанной около треугольника ABC окружности по данным
Слайд 47Решение треугольников
Задача 11
Найти радиус описанной около треугольника ABC окружности по данным
∆ABC-равнобедренный
Слайд 48Решение треугольников
Задача 12
Найти радиус описанной около треугольника ABC окружности по данным
Слайд 49Решение треугольников
Задача 12
Найти радиус описанной около треугольника ABC окружности по данным
ABCD-равнобедренная трапеция
Слайд 50Решение треугольников
Задача 12
Найти радиус описанной около треугольника ABC окружности по данным
∆ABC-равнобедренный
ABCD-равнобедренная трапеция