- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Разработка урока по теме Дифференциальные уравнения
Содержание
- 1. Разработка урока по теме Дифференциальные уравнения
- 2. Цели: Изучить виды простых дифференциальных уравнений.Овладеть навыками решения
- 3. Дифференциальным уравнением называется уравнение, связывающее между собой
- 4. Дифференциальное уравнение называется обыкновенным , если искомая
- 5. Решением (или интегралом) дифференциального уравнения называется такая
- 6. Частным решением дифференциального уравнения называется решение, полученное
- 7. Дифференциальным уравнением первого порядка называется уравнение, вкоторое входят производные (или дифференциалы) не выше первогопорядка.
- 8. 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ1) Разделить переменные2) Проинтегрировать
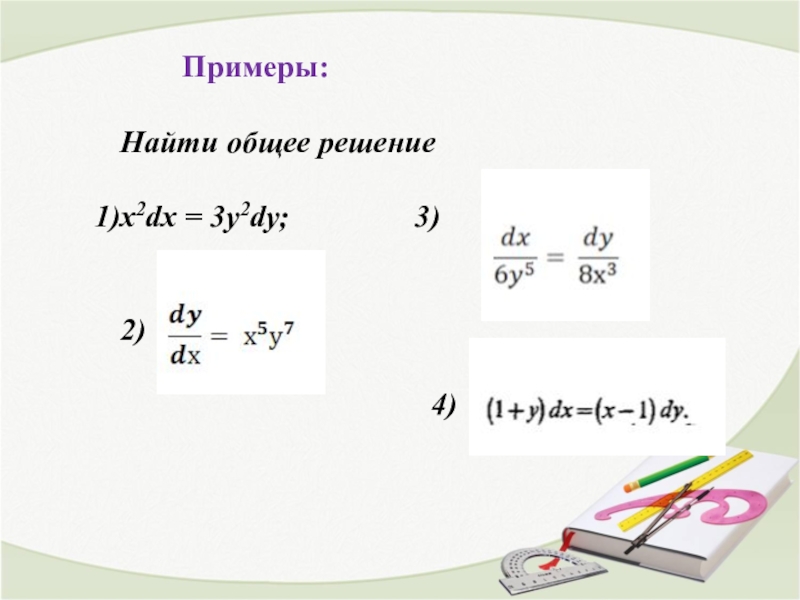
- 9. Примеры:Найти общее решениеx2dx = 3y2dy;
- 10. Примеры:Найти частное решениеsinxdx + ydy= 0, при
- 11. 2. ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКАОднородной функцией
- 12. Однородным уравнением называется уравнение вида:f(x, y)dx=φ(x, y)dyгде
- 13. Примеры: Найти общее решение уравнения
- 14. Найти частное решение уравнения1)2) 3)
- 15. 3. ЛИНЕЙНЫЕ ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
Цели: Изучить виды простых дифференциальных уравнений.Овладеть навыками решения дифференциальных уравнений с разделенными и разделяющимися переменными.Развивать логическое мышление, память, внимание и самостоятельность.
Слайд 2Цели:
Изучить виды простых дифференциальных уравнений.
Овладеть навыками решения дифференциальных уравнений с разделенными
и разделяющимися переменными.
Развивать логическое мышление, память, внимание и самостоятельность.
Развивать логическое мышление, память, внимание и самостоятельность.
Слайд 3Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную х, искомую
функцию у и ее производные или дифференциалы.
F(x, у, у')=0, F(x, у, у'')=0, F(x, у, у', у'', ..., уn)=0.
F(x, у, у')=0, F(x, у, у'')=0, F(x, у, у', у'', ..., уn)=0.
Слайд 4
Дифференциальное уравнение называется обыкновенным , если искомая функция зависит от одного
независимого переменного (х).
Порядком дифференциального уравнения называется порядок старшей
производной , входящей в данное уравнение.
Порядком дифференциального уравнения называется порядок старшей
производной , входящей в данное уравнение.
Слайд 5Решением (или интегралом) дифференциального уравнения называется такая функция, которая обращает это
уравнение в тождество.
Общим решением дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных (С), каков порядок уравнения.
Общим решением дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных (С), каков порядок уравнения.
Слайд 6Частным решением дифференциального уравнения называется решение, полученное из общего при различных
числовых значениях произвольных постоянных.
Интегральная кривая - график частного решения дифференциального уравнения.
Общему решению дифференциального уравнения соответствует совокупность (семейство) всех интегральных кривых.
Интегральная кривая - график частного решения дифференциального уравнения.
Общему решению дифференциального уравнения соответствует совокупность (семейство) всех интегральных кривых.
Слайд 7Дифференциальным уравнением первого порядка называется уравнение, в
которое входят производные (или дифференциалы)
не выше первого
порядка.
порядка.
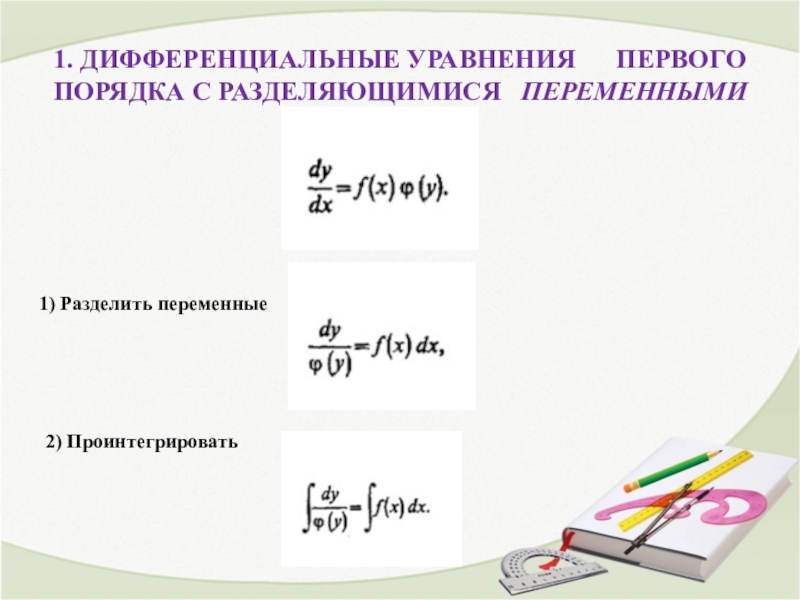
Слайд 81. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
1)
Разделить переменные
2) Проинтегрировать
Слайд 10Примеры:
Найти частное решение
sinxdx + ydy= 0, при у = 4,
х = π/3
уdy = xdx , при у = 4, х = -2
хdy = уdx , при у = 6, х = 2
(1+у)dх = (1-x)dу , при у = 3, х = -2
5)
уdy = xdx , при у = 4, х = -2
хdy = уdx , при у = 6, х = 2
(1+у)dх = (1-x)dу , при у = 3, х = -2
5)
Слайд 112. ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Однородной функцией переменных х и уназывается
функция» все члени которой имеют одинаковую степень.
Например:
Например:
Слайд 12Однородным уравнением называется уравнение вида:
f(x, y)dx=φ(x, y)dy
где f(x, y) и φ(x,
y)-однородые функции одной й той же степени.
Однородное уравнение при помощи подстановки у=их приводится к уравнению с разделяющимися переменными.
Однородное уравнение при помощи подстановки у=их приводится к уравнению с разделяющимися переменными.
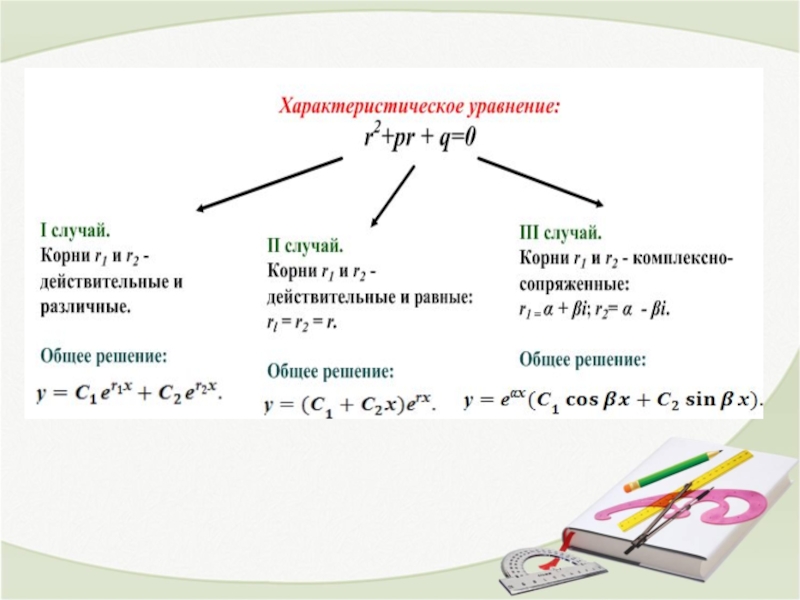
Слайд 153. ЛИНЕЙНЫЕ ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Линейным однородным
дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида:
где р и q-постоянные величины.
где р и q-постоянные величины.