г.о. Балашиха
16.11.2015
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Различные способы решения задач на концентрацию
Содержание
- 1. Различные способы решения задач на концентрацию
- 2. 1. В растворе 40% соли. Если добавить
- 3. В растворе 40% соли. Если добавить 120
- 4. «Правило креста» (конверт Пирсона)
- 5. «Правило креста»m1 - масса первого веществаm2 -
- 6. В растворе 40% соли. Если добавить 120
- 7. 2. Смешали 150 г 30% раствора кислоты
- 8. 3. Сколько нужно взять 10 % раствора
- 9. Слайд 9
- 10. Сколько нужно взять 10 % раствора соли
- 11. 4. Смешали 60% и 10 % раствор
- 12. 5. Сколько воды нужно добавить к 250
- 13. 6 . Сколько сухой соли нужно добавить
- 14. 7. Свежие фрукты содержат
- 15. 8. Первый сплав содержит 5 % меди,
- 16. 9. У некоторого человека были на продажу
1. В растворе 40% соли. Если добавить 120 г соли, процентное содержание соли станет 70%. Сколько граммов соли было в растворе первоначально? 0,7 (x + 120) = 0,4 x + 1200,7 x – 0,4 x =
Слайд 1«Решение задач на концентрацию различными методами»
Жирякова Людмила Викторовна
yчитель математики
МАОУ «Лицей»
Слайд 21. В растворе 40% соли. Если добавить 120 г соли, процентное
содержание соли станет 70%. Сколько граммов соли было в растворе первоначально?
0,7 (x + 120) = 0,4 x + 120
0,7 x – 0,4 x = 120 – 84
0,3 x = 36
x = 120 г 0,4 ∙ 120 = 48 г Ответ : 48 г
Слайд 3В растворе 40% соли. Если добавить 120 г соли, процентное содержание
соли станет 70%.
Сколько граммов соли было в растворе первоначально?
Было
соль
вода
40%
60%
соль
вода
70%
30%
соль
Х У
120 + Х У
Стало
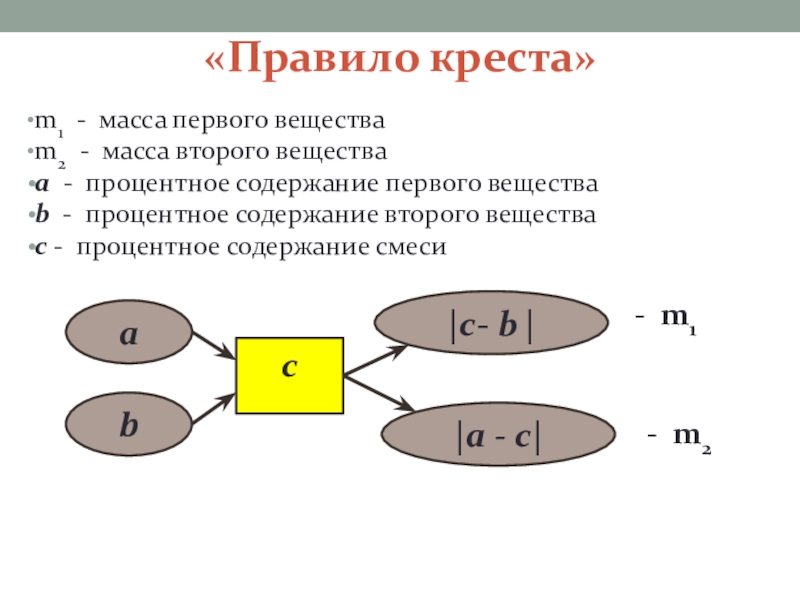
Слайд 5«Правило креста»
m1 - масса первого вещества
m2 - масса второго вещества
a -
процентное содержание первого вещества
b - процентное содержание второго вещества
c - процентное содержание смеси
b - процентное содержание второго вещества
c - процентное содержание смеси
a
b
|c- b |
|a - c|
c
- m1
- m2
Слайд 6В растворе 40% соли. Если добавить 120 г соли, процентное содержание
соли станет 70%. Сколько граммов соли было в растворе первоначально?
x - масса первого вещества
m2 = 120г - масса первого вещества
a = 40 % массовая доля первого вещества
b = 100 % массовая доля третьего вещества
c = 70 % массовая доля смеси
40%
100%
|100 – 70| = 30
|40 –70| = 30
70%
- х
- 120
X = 120 г, 40 % от 120 равно 48 г
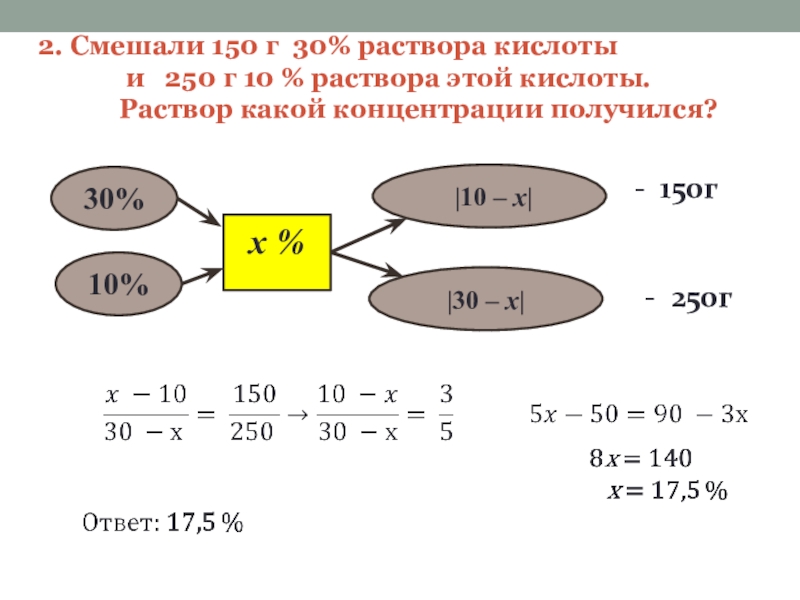
Слайд 72. Смешали 150 г 30% раствора кислоты
и 250 г 10 % раствора этой кислоты.
Раствор какой концентрации получился?
30%
10%
|10 – х|
|30 – х|
x %
- 150г
- 250г
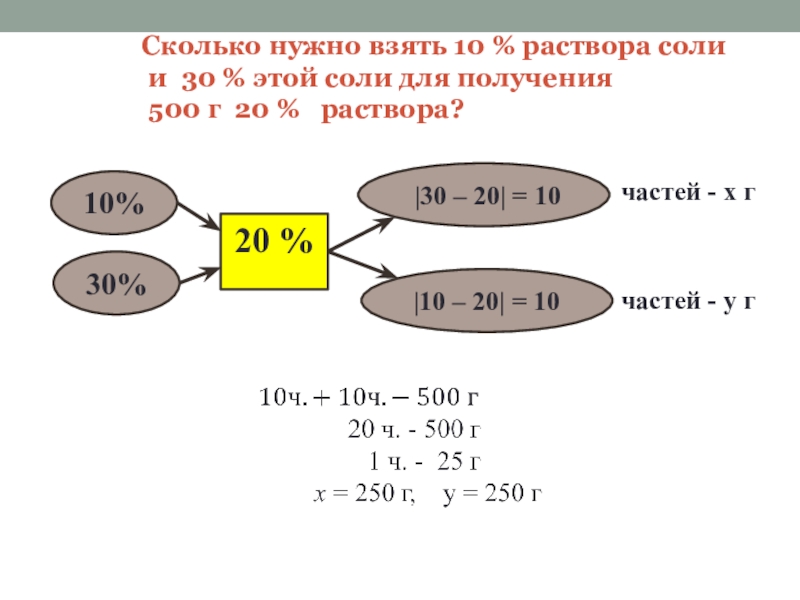
Слайд 83. Сколько нужно взять 10 % раствора соли и 30 %
этой соли для получения 500 г 20 % раствора?
Слайд 9 Сколько нужно взять
10 % раствора соли
и 30 % этой соли для получения
500 г 20 % раствора?
10%
30%
|30 – 20| = 10
|10 – 20| = 10
20 %
частей - х г
частей - у г
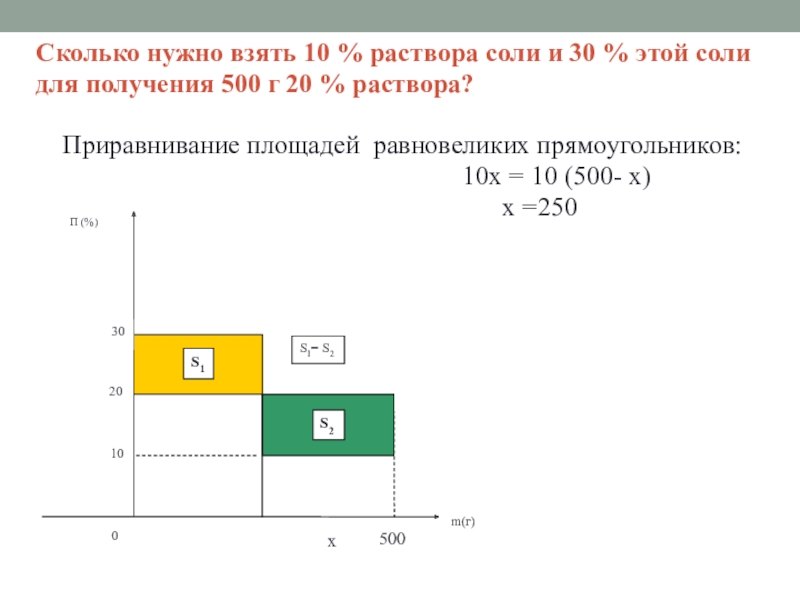
Слайд 10Сколько нужно взять 10 % раствора соли и 30 % этой
соли для получения 500 г 20 % раствора?
Приравнивание площадей равновеликих прямоугольников:
10x = 10 (500- x)
x =250
Слайд 114. Смешали 60% и 10 % раствор кислоты, получив при
этом 300 г 25 % раствора этой кислоты.
Сколько граммов каждого раствора нужно взять?
60%
10%
|25 – 10|= 15
|25 – 60| = 35
25 %
- x г
- y г
Слайд 125. Сколько воды нужно добавить к 250 г раствора соли для
понижения концентрации с 45 % до 10%?
45 %
0 %
|0 – 10| = 10
|45 – 10| = 35
10 %
- 250 г
- х г
Слайд 136 . Сколько сухой соли нужно добавить к 250 г раствора
10 % концентрации для увеличения её до 40%?
10 %
100 %
|100 – 40| = 60
|10 – 40| = 30
40 %
- 250 г
- х г
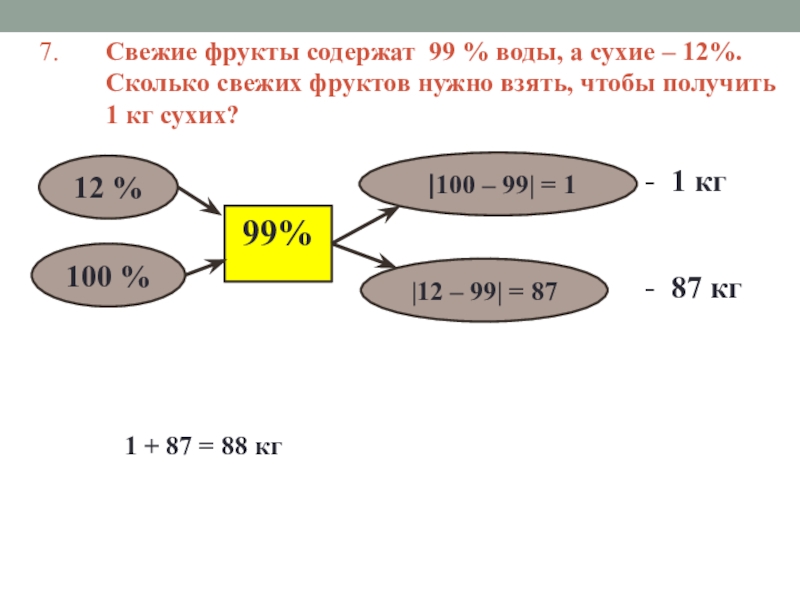
Слайд 147. Свежие фрукты содержат 99 % воды, а
сухие – 12%.
Сколько свежих фруктов нужно взять, чтобы получить
1 кг сухих?
12 %
100 %
|100 – 99| = 1
|12 – 99| = 87
99%
- 1 кг
- 87 кг
1 + 87 = 88 кг
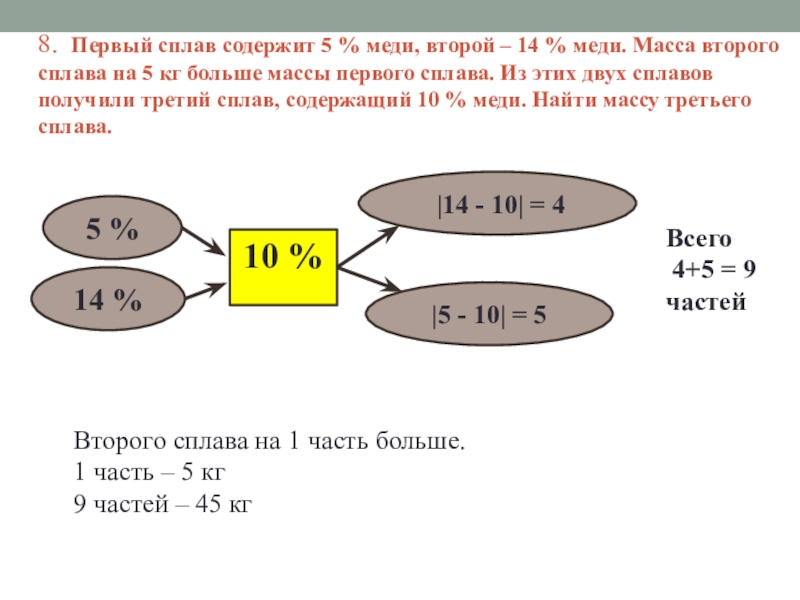
Слайд 158. Первый сплав содержит 5 % меди, второй – 14 %
меди. Масса второго сплава на 5 кг больше массы первого сплава. Из этих двух сплавов получили третий сплав, содержащий 10 % меди. Найти массу третьего сплава.
5 %
14 %
|14 - 10| = 4
|5 - 10| = 5
10 %
Всего
4+5 = 9 частей
Второго сплава на 1 часть больше.
1 часть – 5 кг
9 частей – 45 кг
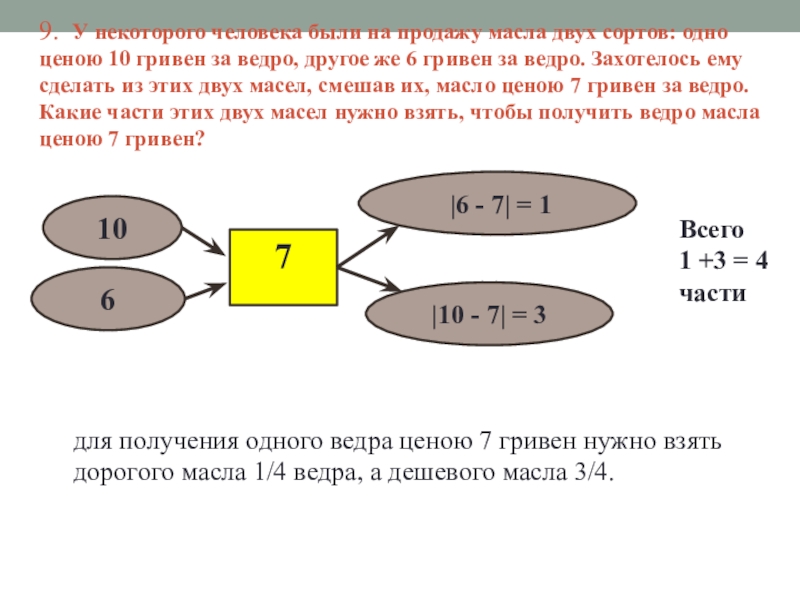
Слайд 169. У некоторого человека были на продажу масла двух сортов: одно
ценою 10 гривен за ведро, другое же 6 гривен за ведро. Захотелось ему сделать из этих двух масел, смешав их, масло ценою 7 гривен за ведро. Какие части этих двух масел нужно взять, чтобы получить ведро масла ценою 7 гривен?
10
6
|6 - 7| = 1
|10 - 7| = 3
7
Всего
1 +3 = 4 части
для получения одного ведра ценою 7 гривен нужно взять дорогого масла 1/4 ведра, а дешевого масла 3/4.
