- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проект Метод координат в математике и географии
Содержание
- 1. Проект Метод координат в математике и географии
- 2. Определение местоположения того или иного предмета на
- 3. Цель проекта:Исследовать и сравнить способы определения «адреса» объекта в географии и математики.
- 4. Задачи проекта: Ответить на следующие вопросы:Кто, когда
- 5. Историческая справка. Во II – III веках
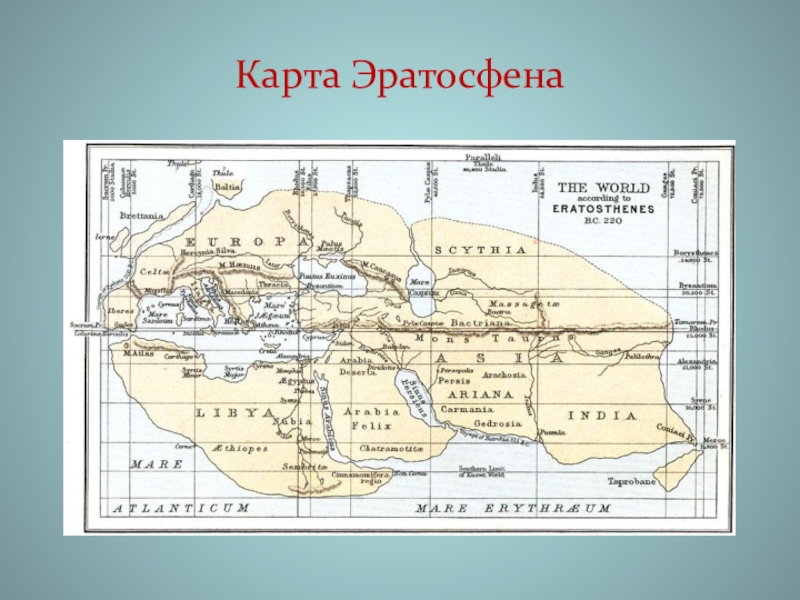
- 6. Карта Эратосфена
- 7. Во II в. до н. э. Гиппарх
- 8. Карта Гиппарха
- 9. Завершил плеяду великих античных астрономов и географов
- 10. 1. География : «geo» – Земля, «grafo»
- 11. Почему географические широта и долгота измеряются в
- 12. Появление алгебры, как ветви математики. В IX
- 13. В XIV в. французский математик Никола Орезм
- 14. Метод координатАлгебраТочка плоскости задается парой чисел М
- 15. Рене Декарт (1596-1650) – французский математик, философ,
- 16. 1. Нужно отметить, что у Декарта еще
- 17. Сравним системы координат в математике и географии.1.
- 18. Полярные и сферические координаты.Полярная система координат включает
- 19. Сферической системой координат пользуются, если необходимо определить
- 20. КОНЦЕПТУАЛЬНАЯ КАРТА ГеографияКартографияСистема координат1. Прямоугольные- географическая
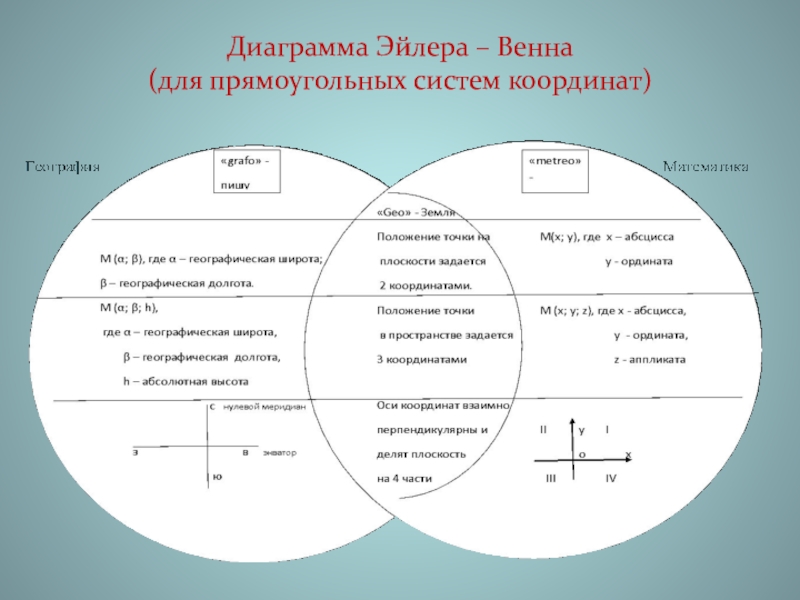
- 21. Диаграмма Эйлера – Венна (для прямоугольных систем координат)
- 22. Диаграмма Эйлера – Венна (для полярных систем координат).
- 23. Выводы:1. Слова «геометрия» и «география» имеют древнегреческое
- 24. Таким образом, понятия «координаты» в географии и
- 25. Литература:1. «География. Справочные материалы». Под ред. Максаковского.-М.,
- 26. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 1Учебный комплекс авторской физико-математической школы-лицея № 61.
ПРОЕКТ
«Метод координат в математике и
Выполнили: учащиеся 7 Б и 7 В классов УК АФМШЛ № 61
Евлашков Даниил
Литтау Роман
Хегай Владимир
Руководитель: Горборукова Н.В.
г. Бишкек – 2012 г.
Слайд 2Определение местоположения того или иного предмета на поверхности Земли или какой-либо точки
«Адрес» в географии – географическая широта;
географическая долгота;
абсолютная высота.
«Адрес» в математике – абсцисса, ордината точки
на координатной плоскости
Слайд 3Цель проекта:
Исследовать и сравнить способы определения «адреса» объекта в географии и
Слайд 4Задачи проекта:
Ответить на следующие вопросы:
Кто, когда и для чего впервые ввел
Существует ли генетическая связь между понятиями «географические координаты» и «координатный метод» в математике? Или это слова-омонимы?
На развитие каких наук оказал влияние метод координат?
Какие еще виды систем координат помимо прямоугольной существуют и используются человеком в настоящее время в практической деятельности?
Слайд 5Историческая справка. Во II – III веках до н. э. меридианы и
Слайд 7Во II в. до н. э. Гиппарх впервые разделил круг на
Слайд 9Завершил плеяду великих античных астрономов и географов Клавдий Птолемей (190 –
Слайд 101. География : «geo» – Земля, «grafo» – пишу.
2. Геометрия: «geo»
Как видно, эти две науки были тесно связаны между собой, их возникновение обусловлено практической деятельностью людей того времени.
Слайд 11Почему географические широта и долгота измеряются в градусах?
Географическая широта – это
Из курса геометрии известно, что дуги измеряются как в линейных величинах, так и в угловых: градусах и радианах.
Географическая долгота – это величина дуги параллели от нулевого меридиана до заданной точки.
Видно, что географические координаты – понятие математическое.
Слайд 12Появление алгебры, как ветви математики. В IX веке узбекский математик и астроном
Слайд 13В XIV в. французский математик Никола Орезм предложил ввести , по
Слайд 14Метод координат
Алгебра
Точка плоскости задается парой чисел М (x;y) - алгебраический объект
Прямая
Геометрия
Точка плоскости - геометрический объект
Слайд 15Рене Декарт (1596-1650) – французский математик, философ, физик и физиолог.
Декарт является
В математике именно ему принадлежит основная заслуга в создании метода координат, который был положен в основу аналитической геометрии.
Слайд 161. Нужно отметить, что у Декарта еще не было того, что
Слайд 17Сравним системы координат в математике и географии.
1. Для определения положения объекта
2. Для определения положения точки на плоскости необходимы 2 координаты: абсцисса и ордината.
3. Параллели и меридианы взаимно перпендикулярны.
4. Оси OX и OY взаимно перпендикулярны.
5. Для определения точки в пространстве требуется 3 – я координата:
абсолютная высота (в географии);
аппликата в математике.
6. Экватор и нулевой меридиан делят поверхность земного шара на 4 части
7. Координатные оси делят плоскость на 4 части, а пространство на 8 частей.
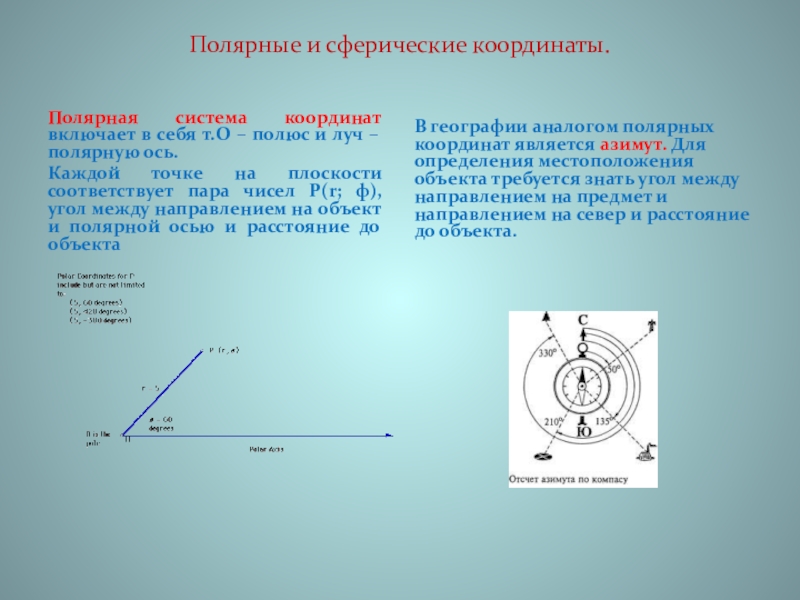
Слайд 18Полярные и сферические координаты.
Полярная система координат включает в себя т.О –
Каждой точке на плоскости соответствует пара чисел Р(r; ф), угол между направлением на объект и полярной осью и расстояние до объекта
В географии аналогом полярных координат является азимут. Для определения местоположения объекта требуется знать угол между направлением на предмет и направлением на север и расстояние до объекта.
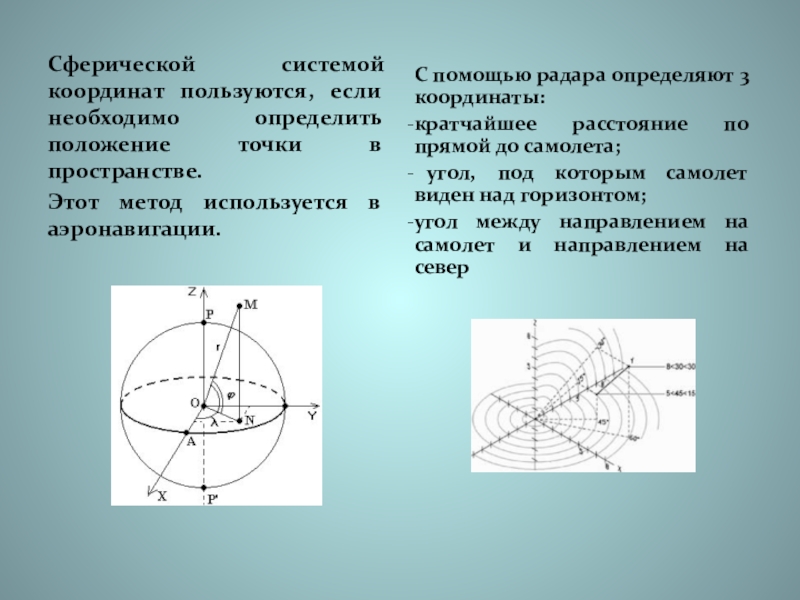
Слайд 19Сферической системой координат пользуются, если необходимо определить положение точки в пространстве.
Этот
С помощью радара определяют 3 координаты:
кратчайшее расстояние по прямой до самолета;
угол, под которым самолет виден над горизонтом;
угол между направлением на самолет и направлением на север
Слайд 20КОНЦЕПТУАЛЬНАЯ КАРТА
География
Картография
Система координат
1. Прямоугольные
- географическая широта
- географическая долгота
- абсолютная высота
2.
- азимут
- расстояние до объекта
- абсолютная высота
Математика
Алгебра Геометрия
Метод координат
1. Прямоугольные
- абсцисса
- ордината
- аппликата
2. Полярные
- угол поворота
- расстояние от начала координат до точки
Слайд 23Выводы:
1. Слова «геометрия» и «география» имеют древнегреческое происхождение и связаны с
2. Географические широта и долгота измеряются в градусах, так как представляют собой дуги окружностей, стягивающих центральные углы, т. е. являются математическими величинами.
3. И в математике, и в географии используются как прямоугольные, так и полярные координаты.
4. В прямоугольных системах координат оси (экватор и нулевой меридиан, оси OX и OY) взаимно перпендикулярны и делят плоскость на 4 части: Северное, Южное, Западное и Восточное полушария в географии и I, II, III, IV квадранты.
5. Положение точки на плоскости задается 2 координатами: широтой и долготой в географии, абсциссой и ординатой в математике.
6. При определении положения объекта в пространстве появляется третья координата: абсолютная высота в географии и аппликата в математике.
7.Для задания полярных координат необходимы: точка отсчета, угол поворота, расстояние от полюса до заданной точки.
Слайд 24Таким образом, понятия «координаты» в географии и математике не являются словами-омонимами.
Слайд 25Литература:
1. «География. Справочные материалы». Под ред. Максаковского.-М., «Просвещение», 1989.
2. Прочухаев В.Г.
3. Маслов А.В. «Геодезия».- М., Недра, 1972
4. Знаменский М.А. «Измерительные работы на местности».- М., «Учпедгиз», 1986.
5. Энциклопедический словарь юного математика. Сост. Л.П. Савин, - М., «Педагогика», 1985.
6. https://www.10489.jpg
7. https://www.dekart2d.gif
8. https.//www.image100.jpg
9. https.//www.edumedia-sciences.com
10. https.//www.k08-latlon.gif