- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Признаки параллельности прямых
Содержание
- 1. Признаки параллельности прямых
- 2. Цель урока Вспомнить, какие прямые называются
- 3. Какие прямые называются параллельными? Посмотрим на схемуУкажите
- 4. Доказательство:Пусть при пересечении двух прямых a и
- 5. Второй признак параллельности прямыхЕсли при пересечении двух
- 6. ЗадачаΔАВС р/бВС основание ΔАВСДоказать, что α ׀׀bТак
- 7. Выполнить самостоятельно34Углы 3 и 4 односторонние ив
- 8. Подведение итогов урокаВ чем заключается первый признак
- 9. Математическое доминоL1 и L4L2 и L5L1 и L2L3 и L2L4 и L3
- 10. Домашнее заданиеРабочая тетрадь № 88, 89,90,91
Слайд 1Признаки параллельности прямых
Открытый урок по геометрии в 7 классе, учителя математики
Слайд 2Цель урока
Вспомнить, какие прямые называются параллельными.
Какие пары
Изучить признаки параллельности прямых
Слайд 3Какие прямые называются параллельными?
Посмотрим на схему
Укажите накрест лежащие углы и
Укажите односторонние углы и вспомните их свойство:
Укажите соответственные углы и вспомните свойство этих углов:
:
1
2
3
4
5
6
7
8
Две прямые на плоскости называются параллельными, если они не пересекаются
Слайд 4Доказательство:
Пусть при пересечении двух прямых a и b секущей f накрест
Точка О является серединой отрезка АВ, проведем из этой точки перпендикуляр ОН к прямой а. На прямой b от точки В отложим отрезок ВН1, равный отрезку АН.
Треугольник ОНА и ОН1В равны по двум сторонам и углу между ними (АО=ОВ, АН=ВН1, и ), следовательно
Из равенства углов 3 и 4 следует, что точка Н1 лежит на продолжении прямой ОН. А из равенства углов 5 и 6 следует, что ∟6 – прямой (т.к. ∟5-прямой).
Таким образом прямые a и b перпендикулярны прямой НН1, поэтому параллельны.
Для доказательства параллельности прямых необходимо знать 3 признака:
Первый признак параллельности прямых
Если при пересечении двух прямых секущей накрест лежащие углы равны. То эти прямые параллельны
a
b
f
О
Н
Н1
В
А
1
2
3
4
5
6
Слайд 5Второй признак параллельности прямых
Если при пересечении двух прямых секущей соответственные углы
Доказательство:
Пусть при пересечении двух прямых a и b секущей f соответственные углы равны:
Так как углы 2 и 3 вертикальные, то они равны ∟2=∟3, то ∟1 =∟2= ∟3, а ∟1= ∟3 накрест лежащие, Следовательно прямые a и b параллельны
Третий признак параллельности прямых
Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то эти прямые параллельны.
Доказательство:
Пусть при пересечении двух прямых a и b секущей f сумма односторонних углов ∟1+∟4=1800. Так как ∟3 и ∟4 смежные, то ∟3+∟4= 1800, из этих равенств следует, накрест лежащие углы 1 и 3 равны:∟1=∟3, а рас накрест лежащие углы равны, то прямые a и b параллельны.
a
b
f
1
2
3
4
Слайд 6
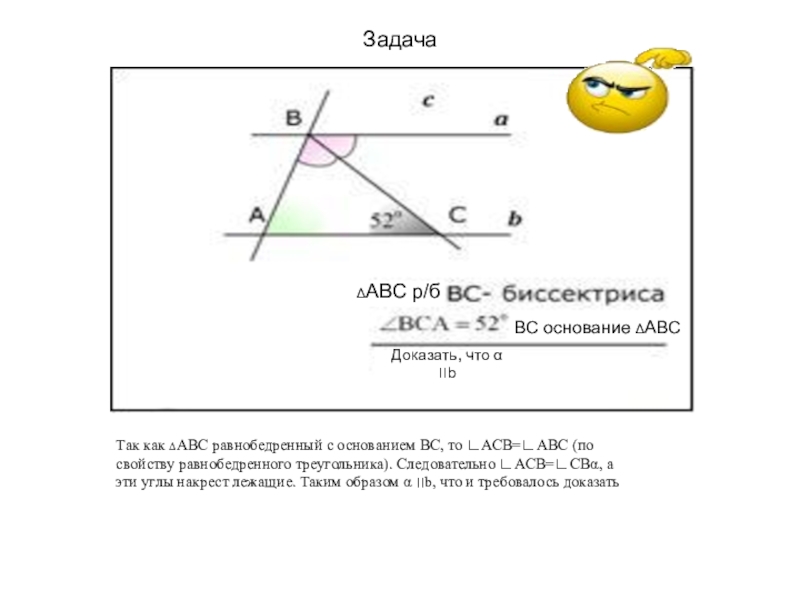
Задача
ΔАВС р/б
ВС основание ΔАВС
Доказать, что α ׀׀b
Так как ΔАВС равнобедренный с
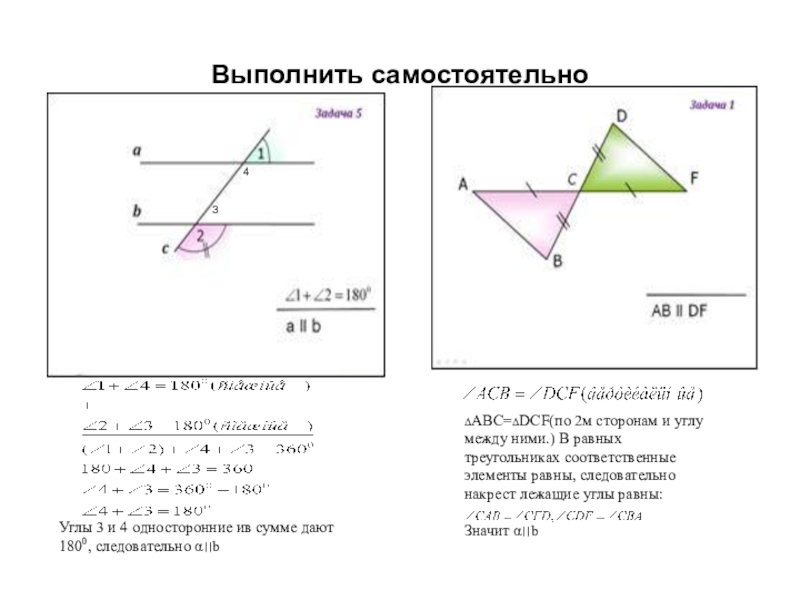
Слайд 7Выполнить самостоятельно
3
4
Углы 3 и 4 односторонние ив сумме дают 1800, следовательно
ΔАВС=ΔDCF(по 2м сторонам и углу между ними.) В равных треугольниках соответственные элементы равны, следовательно накрест лежащие углы равны:
Значит α׀׀b
Слайд 8Подведение итогов урока
В чем заключается первый признак параллельных прямых?
В чем заключается
В чем заключается третий признак параллельных прямых?