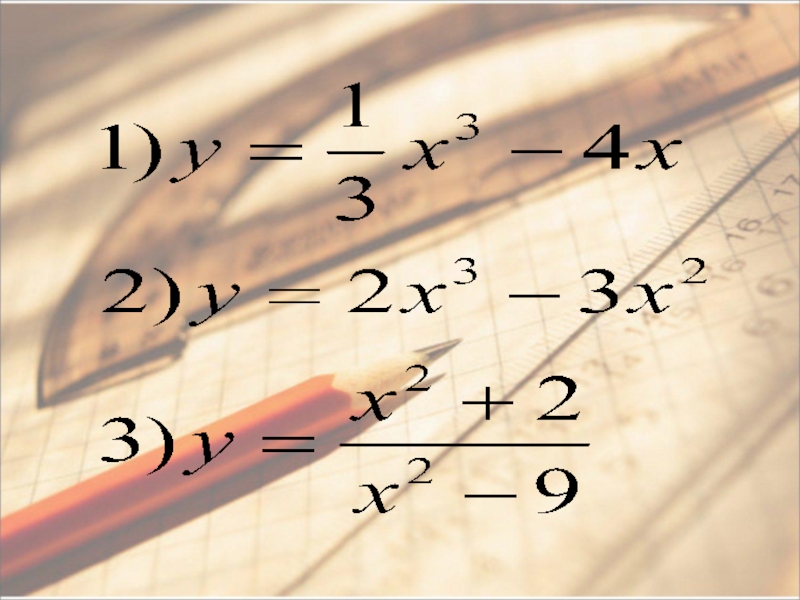- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Применение производной к построению графиков функции
Содержание
- 1. Применение производной к построению графиков функции
- 2. Тема занятия. Применение производной к построению графиков функции.
- 3. Цель занятия: Систематизировать ранее изученный материал для
- 4. Повторение пройденного материала;Вспомним основные понятия и определения, необходимые для исследования функции и построению ее графика.
- 5. Схема исследования и построения графика функции.
- 6. Промежутки монотонности функции ( возрастания и
- 7. Применение производной к построению графиков функций.
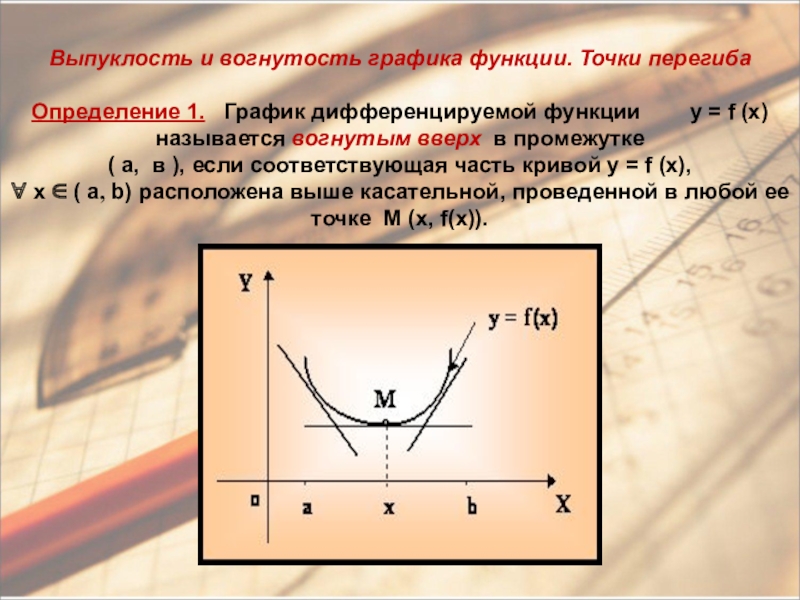
- 8. Выпуклость и вогнутость графика функции. Точки перегиба
- 9. Определение 2. График дифференцируемой функции y = f
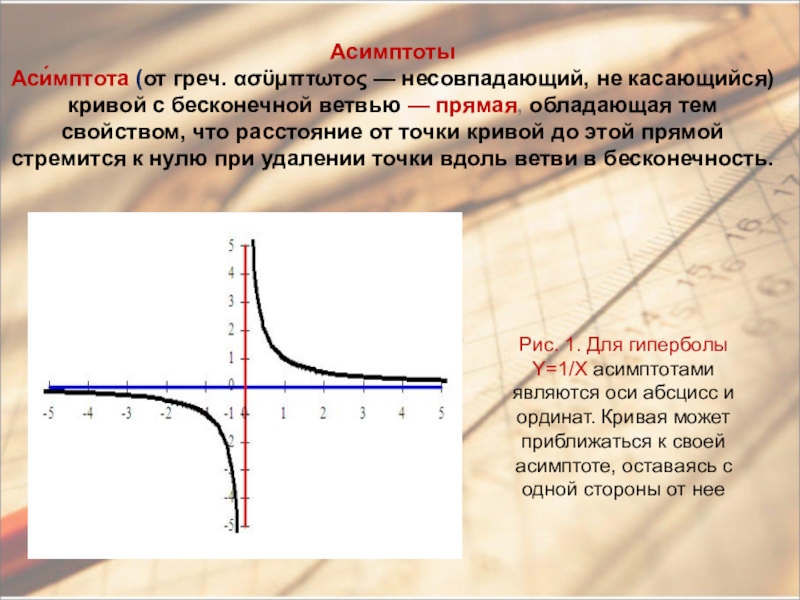
- 10. Асимптоты Аси́мптота (от греч. ασϋμπτωτος — несовпадающий, не
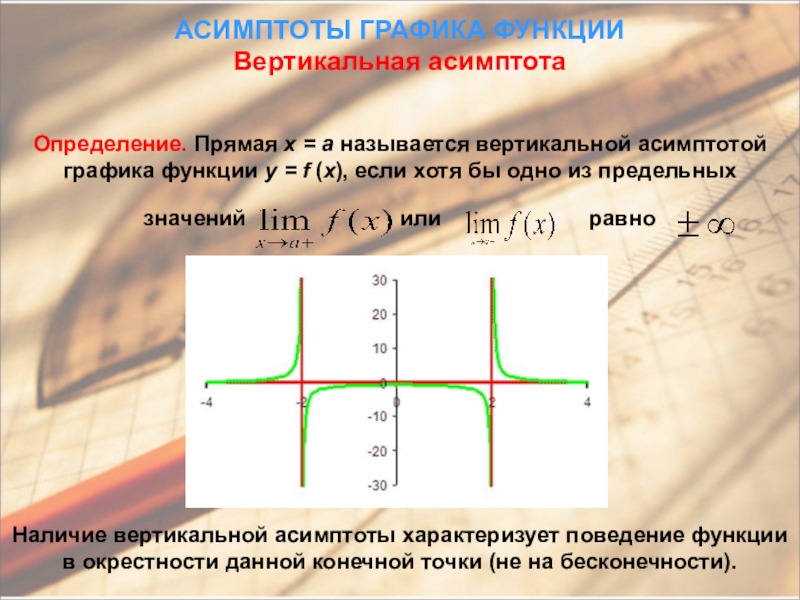
- 11. АСИМПТОТЫ ГРАФИКА ФУНКЦИИ Вертикальная асимптота
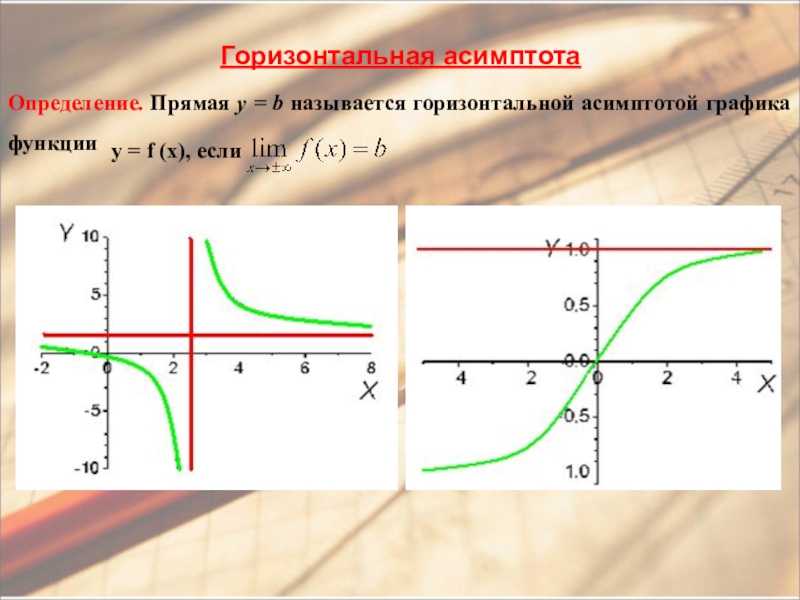
- 12. Горизонтальная асимптотаОпределение. Прямая y = b называется
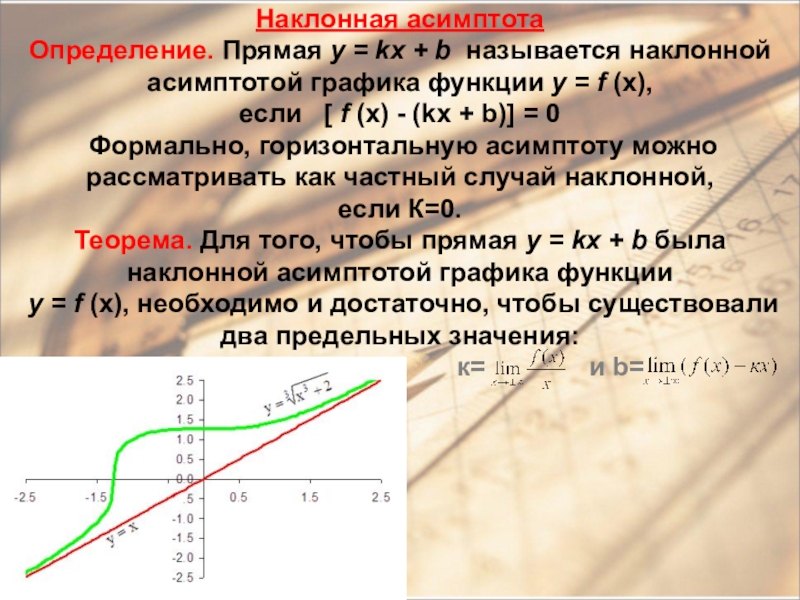
- 13. Наклонная асимптота Определение. Прямая y = kx
- 14. Построение графиков функций.
- 15. Решение :
- 16. Слайд 16
- 17. x
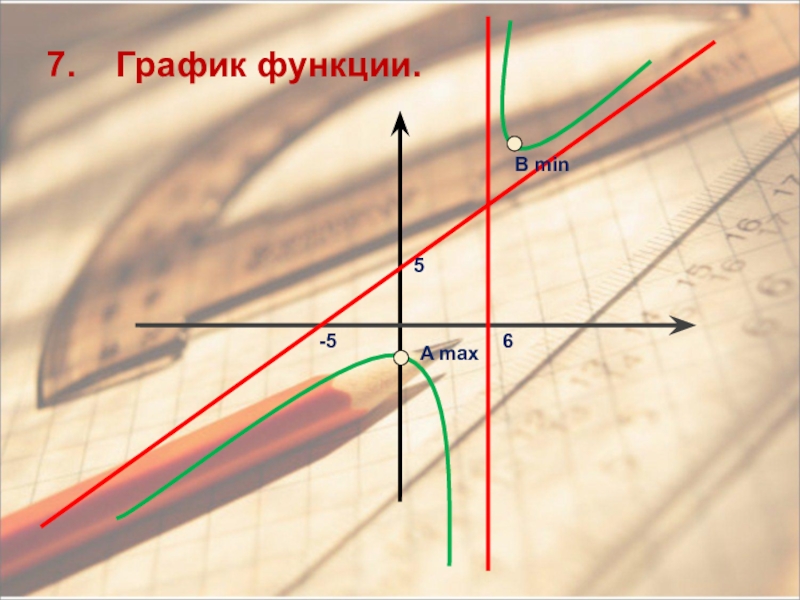
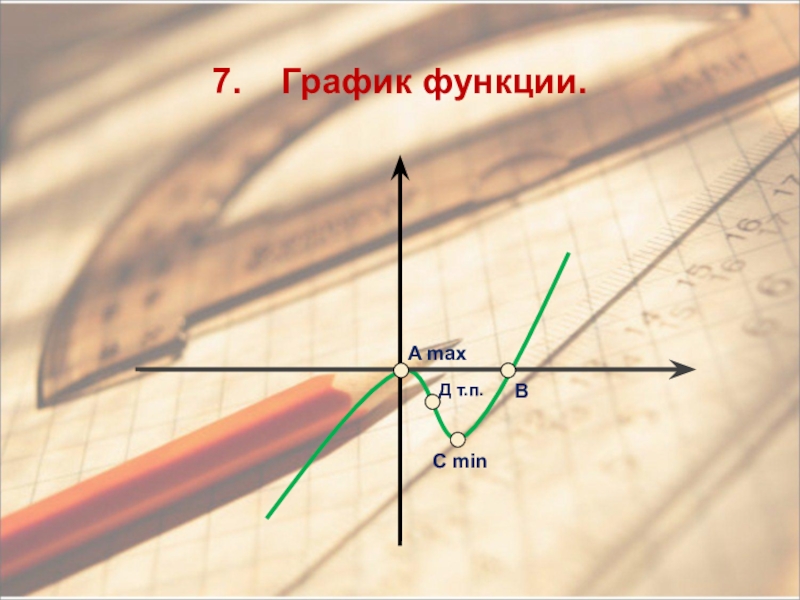
- 18. A max7. График функции. -565В min
- 19. Самостоятельная исследовательская работа студентов.
- 20. Построение графиков функций.Применяя полученные знания, исследовать функцию с помощью производной и построить ее график.
- 21. Слайд 21
- 22. Проверим выполненные задания.
- 23. Слайд 23
- 24. X
- 25. X
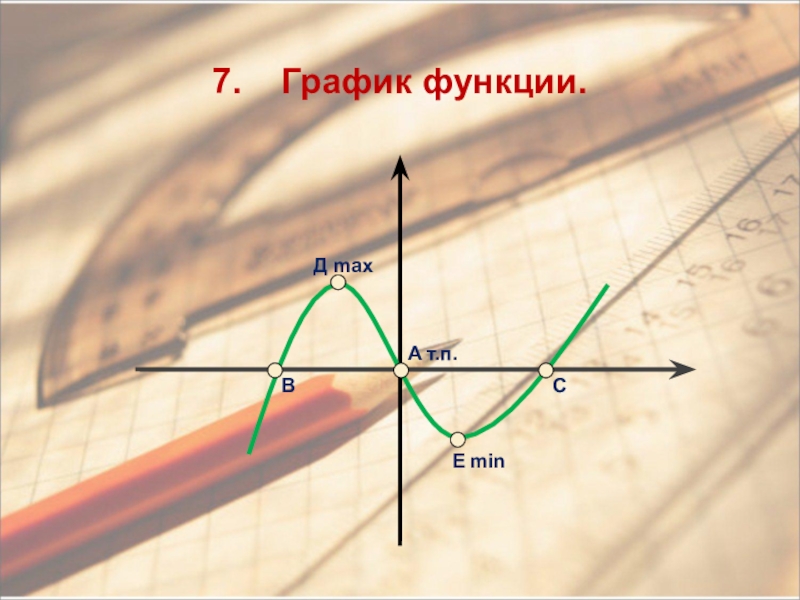
- 26. 7. График функции. BД maxA т.п.E minC
- 27. Решение:
- 28. XX
- 29. A maxC minB7. График функции. Д т.п.
- 30. Решение :
- 31. Слайд 31
- 32. X
- 33. Точек перегиба нет.X
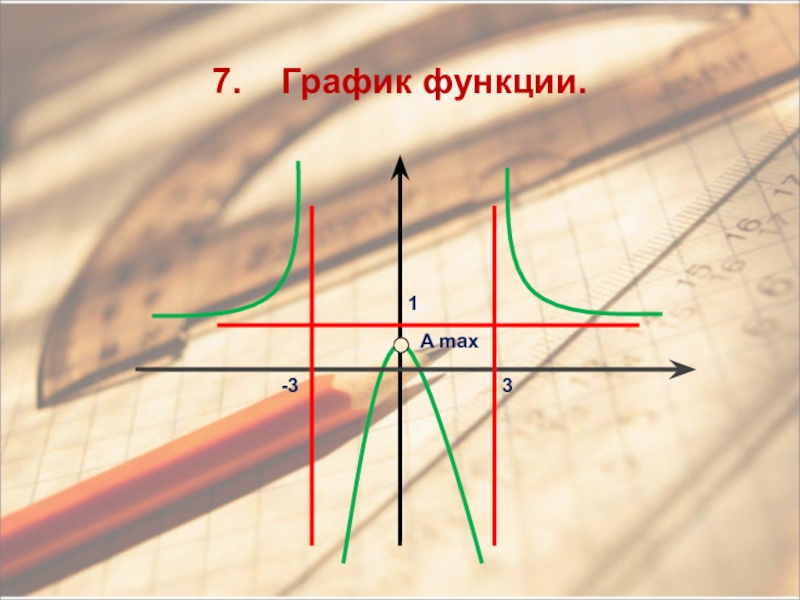
- 34. A max7. График функции. -331
- 35. Итоги урока.Для получения оценки «3» необходимо выполнить
- 36. Домашнее задание:Исследовать функции и построить их графики (задания не выполненные на уроке)
Слайд 1Урок подготовлен
Преподавателем математики
ГБОУ Колледжа автомобильного транспорта №9
Саруль Т.Л.
Слайд 3Цель занятия: Систематизировать ранее изученный материал для исследования и построения графиков
Знания и навыки студентов.
-знать производные элементарных функций и правила дифференцирования;
-знать признак возрастания ( убывания) функции;
-знать определения стационарных и критических точек, точек максимума и минимума;
-знать признак выпуклости( вогнутости) графика функции, понятие точки перегиба;
-знать алгоритм исследования и построения графика функции с помощью производной;
-уметь применять полученные знания для построения графиков функций на основе предварительного проведенного исследования функции в соответствии с планом.
Слайд 4Повторение пройденного материала;
Вспомним основные понятия и определения, необходимые для исследования функции
Слайд 6 Промежутки монотонности функции ( возрастания и убывания) Если во всех
Слайд 7Применение производной к построению графиков функций. Теорема Ферма. Если хо-точка экстремума дифференцируемой
Слайд 8Выпуклость и вогнутость графика функции. Точки перегиба Определение 1. График дифференцируемой функции
Слайд 9Определение 2. График дифференцируемой функции y = f (x) , ∀ x ∈
Теорема 1. (Достаточные условия выпуклости графика)
Î
Если для дважды дифференцируемой функции
y = f(x) вторая производная f″ (x) > 0 , ∀ x ∈ ( a, b) , то график этой функции выпуклый вниз в данном промежутке.
2. Если f″ (x) < 0, x ∈ ( a, b ), то график у = f (x) выпуклый вверх.
Слайд 10Асимптоты Аси́мптота (от греч. ασϋμπτωτος — несовпадающий, не касающийся) кривой с бесконечной ветвью
Рис. 1. Для гиперболы Y=1/X асимптотами являются оси абсцисс и ординат. Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее
Слайд 11АСИМПТОТЫ ГРАФИКА ФУНКЦИИ Вертикальная асимптота Определение. Прямая x = a называется вертикальной
Наличие вертикальной асимптоты характеризует поведение функции в окрестности данной конечной точки (не на бесконечности).
Слайд 12Горизонтальная асимптота
Определение. Прямая y = b называется горизонтальной асимптотой графика функции
y = f (х), если
Слайд 13Наклонная асимптота Определение. Прямая y = kx + b называется наклонной асимптотой
Слайд 14Построение графиков функций. Рассмотрим полную схему исследования функции и построения ее графика
Слайд 20Построение графиков функций.
Применяя полученные знания, исследовать функцию с помощью производной и
Слайд 35Итоги урока.
Для получения оценки «3» необходимо выполнить задания 1 или 2;
Для
Для получения оценки «5» необходимо выполнить любое из заданий 1 или 2 и задание 3.