- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Приложение к курсу Наглядная геометрия 6 класс
Содержание
- 1. Приложение к курсу Наглядная геометрия 6 класс
- 2. Цели работы:Выяснение существования иной, отличной от школьной
- 3. Георг Александр Пик (1859-1942) австрийский математикГеорга, который
- 4. Широкую известность получила открытая им в 1899
- 5. В — количество целочисленных точек внутри многоугольника Г — количество
- 6. Применение формулы ПикаНесмотря на различие форм представленных
- 7. Применение формулы ПикаДля многоугольника, изображенного на рисунке,
- 8. На клетчатой бумаге с клетками размером 1
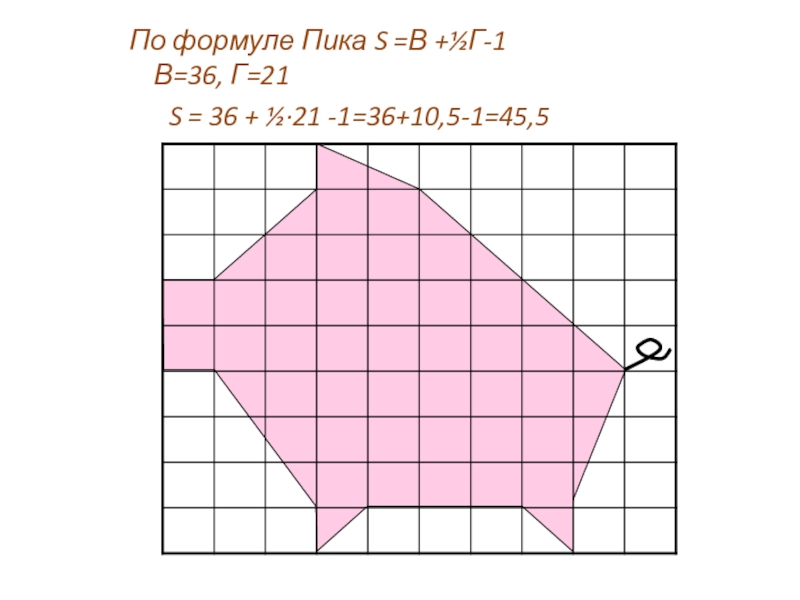
- 9. По формуле Пика S =В +½Г-1 В=36, Г=21 S = 36 + ½·21 -1=36+10,5-1=45,5
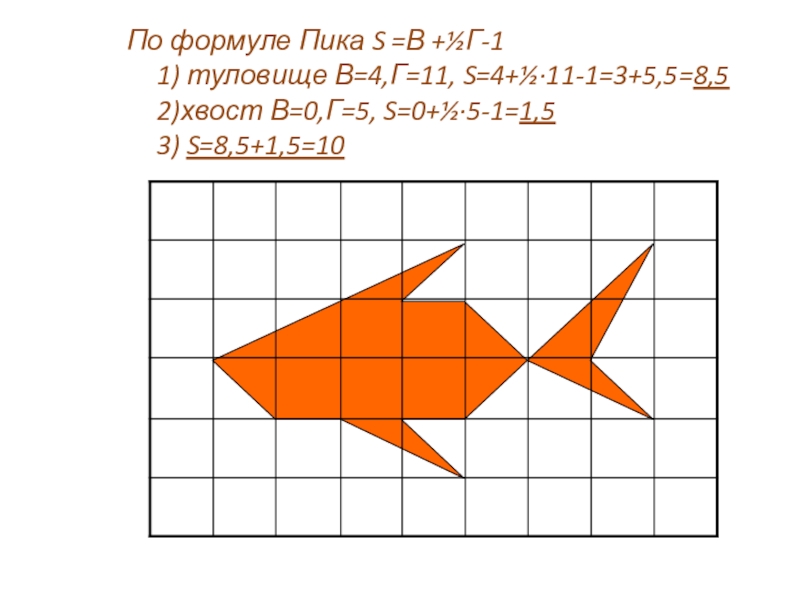
- 10. По формуле Пика S =В +½Г-1 1) туловище В=4,Г=11, S=4+½·11-1=3+5,5=8,5 2)хвост В=0,Г=5, S=0+½·5-1=1,5 3) S=8,5+1,5=10
Цели работы:Выяснение существования иной, отличной от школьной программы, формулы нахождения площади решетчатого многоугольника.Нахождение области применения искомой формулы.
Слайд 1Формула Пика
Приложение к курсу «НАГЛЯДНАЯ ГЕОМЕТРИЯ»
МБОУ СОШ №182 г. Новосибирска
Учитель математики:
Небольсина Евгения Александровна
Слайд 2Цели работы:
Выяснение существования иной, отличной от школьной программы, формулы нахождения площади
решетчатого многоугольника.
Нахождение области применения искомой формулы.
Нахождение области применения искомой формулы.
Слайд 3
Георг Александр Пик (1859-1942) австрийский математик
Георга, который был одарённым ребёнком, обучал
отец, возглавлявший частный институт. В 16 лет Георг окончил школу и поступил в Венский университет. В 20 лет получил право преподавать физику и математику.
В Немецком университете в Праге Георг Пик в 1900—1901 годах занимал пост декана философского факультета.
В Немецком университете в Праге Георг Пик в 1900—1901 годах занимал пост декана философского факультета.
Пик и физик Антон Лампа были главными инициаторами назначения Альберта Эйнштейна профессором в университет, и благодаря их усилиям Эйнштейн, с которым Пик впоследствии сдружился, в 1911 году возглавил кафедру теоретической физики в Немецком университете в Праге.
Слайд 4Широкую известность получила открытая им в 1899 году теорема Пика для
расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники.
Круг математических интересов Пика был чрезвычайно широк. В частности, им написаны работы в области функционального анализа и дифференциальной геометрии, эллиптических и абелевых функций, теории дифференциальных уравнений и комплексного анализа, всего более 50 тем. С его именем связаны матрица Пика, интерполяция Пика — Неванлинны, лемма Шварца — Пика.
Слайд 5 В — количество целочисленных точек внутри многоугольника
Г — количество целочисленных точек на границе
многоугольника.
Формула Пика (или теорема Пика) — классический результат комбинаторной геометрии и геометрии чисел, согласно которому площадь многоугольника с целочисленными вершинами равна
S=В + Г/2 − 1
Формула выполняется, если вершины многоугольника находятся в точках целочисленной решётки.
Слайд 6Применение формулы Пика
Несмотря на различие форм представленных фигур, все они имеют
одинаковую площадь:
В = 1, Г = 5, S = В + Г/2 − 1 = 2,5
В = 1, Г = 5, S = В + Г/2 − 1 = 2,5
В частности, площадь треугольника с вершинами в узлах и не содержащего узлов ни внутри, ни на сторонах (кроме вершин), равна 1/2. Этот факт даёт геометрическое доказательство формулы для разницы подходящих дробей цепной дроби.
Слайд 7Применение формулы Пика
Для многоугольника, изображенного
на рисунке, В=23, Г=7.
Поэтому S=
23+3,5+1=27,5 клеток
Понятно, что площади треугольника, параллелограмма или трапеции проще и быстрее находить по соответствующим формулам. А вот когда дан многоугольник с количеством углов 5 и более, формула подсчета площади с вершинами в узлах сетки становится универсальной.
Вообще, формула Пика очень удобна, когда сложно догадаться, как разбить фигуру на удобные многоугольники или достроить.
Слайд 8На клетчатой бумаге с клетками размером 1 см на 1 см изображены
фигуры (см. рисунок). Найдите их площади в квадратных сантиметрах.
Применение формулы Пика
В – 5; Г – 14, то 5+14:2-1=11 кв.см
В-14, Г-10,то 14+10:2-1=18 кв.см
В-9, Г-12, тогда: 9+12:2-1=14 кв.см
Слайд 10По формуле Пика S =В +½Г-1 1) туловище В=4,Г=11, S=4+½·11-1=3+5,5=8,5 2)хвост В=0,Г=5, S=0+½·5-1=1,5 3)
S=8,5+1,5=10
