- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Презинтация на тему Сложение и вычетание векторов
Содержание
- 1. Презинтация на тему Сложение и вычетание векторов
- 2. Сумма двух векторовРассмотрим пример: Петя из
- 3. Сумма двух векторовВекторы можно складывать – в
- 4. Законы сложения векторов
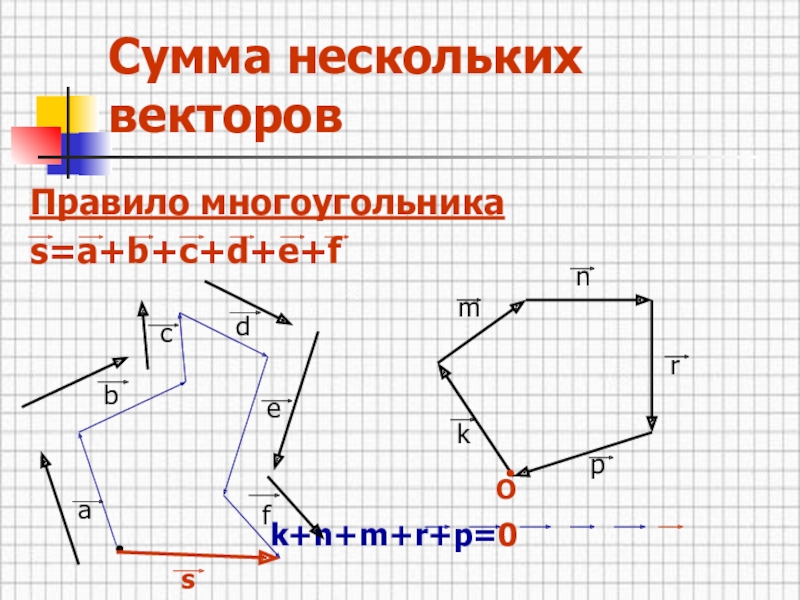
- 5. Сумма нескольких векторовПравило многоугольникаs=a+b+c+d+e+f k+n+m+r+p=0 abcdefskmnrpO
- 6. Противоположные векторы Пусть
- 7. Вычитание векторовТакже можно найти разность двух векторов
- 8. Вычитание векторов–
- 9. Умножение вектора на число
- 10. Умножение вектора на число Для любых чисел
- 11. Решение задач№335№337№347
Слайд 2Сумма двух векторов
Рассмотрим пример:
Петя из дома(D) зашел к Васе(B),
В результате этих двух перемещений, которые можно представить векторами DB и BK, Петя переместился из точки D в К, т.е. на вектор DК:
DK=DB+BK.
Вектор DK называется суммой векторов DB и BK.
D
B
K
Слайд 3Сумма двух векторов
Векторы можно складывать – в результате получается вектор. При
1) При применении правила треугольника один из векторов откладывают от конца другого, т.е. :
2) При применении правила параллелограмма оба вектора откладывают из общей начальной точки, т.е. , где F – вершина параллелограмма, противоположная общей начальной точке векторов.
Слайд 6Противоположные векторы
Пусть а – произвольный ненулевой
Определение. Вектор b называется противоположным вектору а, если а и b имеют равные длины и противоположно направлены.
a = АВ, b = BA
Вектор, противоположный вектору c, обозначается так: -c.
Очевидно, с+(-с)=0 или АВ+ВА=0
А
B
a
b
c
-c
Слайд 7Вычитание векторов
Также можно найти разность двух векторов – в результате получается
Слайд 9Умножение
вектора на число
Определение. Произведением ненулевого
противоположно направлены при k<0.
Произведением нулевого вектора на любое число считается нулевой вектор.
Для любого числа k и любого вектора а векторы а и ka коллинеарны.
а
-2a
3а
Слайд 10Умножение
вектора на число
Для любых чисел k, n и любых векторов
(kn) а = k (na) (сочетательный закон)
(k+n) а = kа + na (второй распределительный закон)
K ( а+ b ) = kа + kb (первый распределительный закон)
Свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях. Например,
p = 2( a – b) + ( c + a ) – 3( b – c + a ) =
= 2a – 2b + c + a – 3b + 3c – 3a = - 5b + 4c