- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад творческая работа Галухиной Алёны
Содержание
- 1. Презентация творческая работа Галухиной Алёны
- 2. 1. Узнать историю возникновения квадратов.2. Познакомиться поближе
- 3. Задачи проекта1.Познакомиться с магическими квадратами.2.Научиться правильно и
- 4. История возникновения магических квадратов
- 5. Возникновение магических квадратов относится к глубокой древности.
- 6. Таблица Ло Шу- состоит из 9 клеток:
- 7. Впервые изображение встречается на гравюре «Меланхолия» немецкогохудожника
- 8. Альбрехт Дюрер Гравюра “Меланхолия”1514 год1632135101189671241
- 9. Проверим достоверность квадрата А.Дюрера 16325101196716+3+2+5+10+11+8=12=9+6+7+4151413812113=4+15+14+1=34Найдем сумму цифр в каждой строке343434
- 10. 16325101196716+10+7+13+11+6+4=415141381211=3434Найдем сумму цифр в каждой диагонали
- 11. 16325101196716+3+5+2+13+11+8=7=10+11+6+4151413812110=9+6+4+15=7+12+14+1=3434343434Найдем сумму цифр в каждом квадрате 2×2
- 12. Так же бывают и другие виды
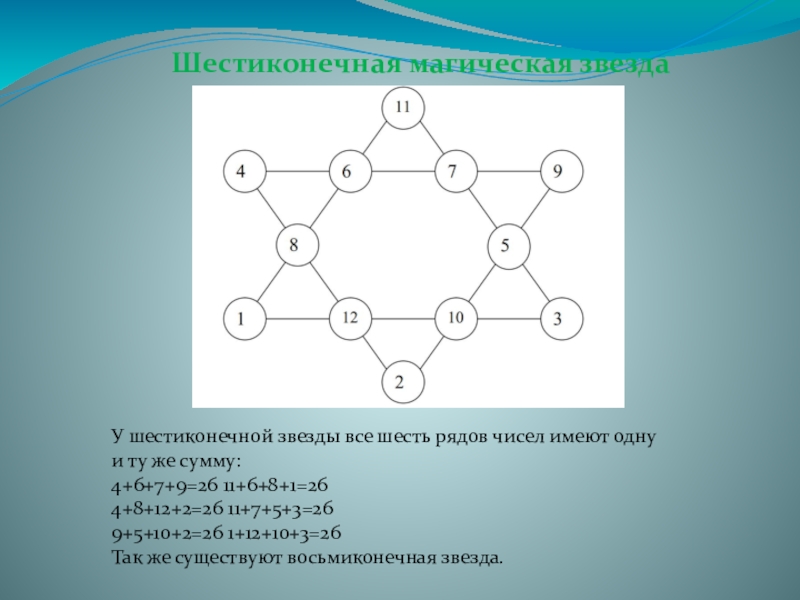
- 13. Шестиконечная магическая звездаУ шестиконечной звезды все шесть
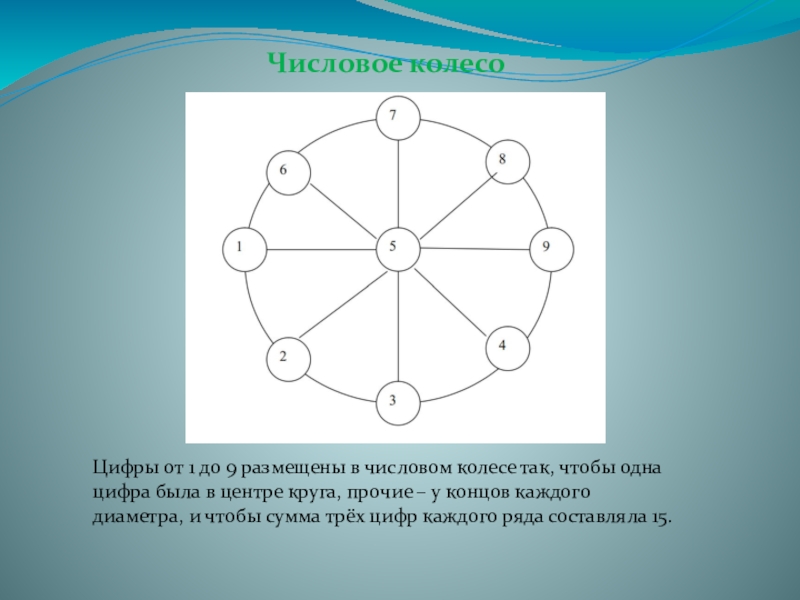
- 14. Числовое колесо Цифры от 1 до
- 15. Магический циферблатЦиферблат разделён на 6 частей любой
- 16. Эту игру, также известную как магический квадрат
- 17. Sudoku - диагональ. В этих sudoku цифры
- 18. Sudoku - диагональ. В этих sudoku цифры
- 19. Классические Sudoku. Обычные Sudoku 9х9.Например:
- 20. Как построить магический квадрат
- 21. Построение магического квадрата четвёртого порядкаПроведём диагонали квадрата
- 22. Практические задания
- 23. 1. Магический квадратРасставьте 6 цифр от 1
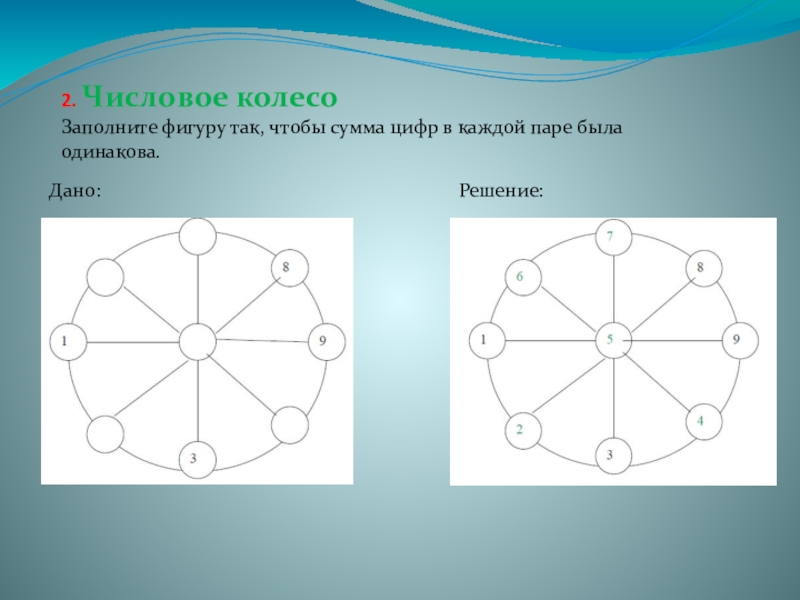
- 24. 2. Числовое колесоЗаполните фигуру так, чтобы сумма цифр в каждой паре была одинакова.Решение:Дано:
- 25. Список литературы1. Аллан Рей, Вилльямс Мартин «Математика
Слайд 1Математические
магические квадраты
Выполнила:
Учащаяся 7 класса
МКОУ Елизаровская ООШ
Галухина Алёна
Слайд 21. Узнать историю возникновения квадратов.
2. Познакомиться поближе с популярной игрой судоку.
3.
Цели проекта
Слайд 3Задачи проекта
1.Познакомиться с магическими квадратами.
2.Научиться правильно и быстро заполнять магические квадраты.
3.Узнать,
Слайд 5Возникновение магических квадратов относится к глубокой древности. Согласно легенде, во времена
Слайд 6Таблица Ло Шу- состоит из 9 клеток: 3 строк и 3
Слайд 7Впервые изображение встречается на гравюре «Меланхолия» немецкого
художника Альбрехта Дюрера (1514). Этот
4 строк и 4 столбцов, заполненных натуральными числами от 1 до 16. В нем сумма чисел по каждой строке, каждому столбцу и двум диагоналям равна 34. Средние числа в нижней строке (15 и 14) означают дату 1514 — год издания этой гравюры А. Дюрера.
Этот магический квадрат замечателен еще и
другими интересными свойствами: в нем одному и
тому же числу (34) равна сумма не только чисел,
стоящих в строках, столбцах и двух диагоналях, но и
суммы чисел, стоящих в квадратах из четырех
клеток, расположенных по углам и в середине, а
также сумма чисел, стоящих в вершинах этого
магического квадрата, следовало бы называть как-
нибудь иначе, например волшебными,
сверхмагическими и т.п.
Слайд 9Проверим достоверность квадрата А.Дюрера
16
3
2
5
10
11
9
6
7
16+
3+
2+
5+
10+
11+
8=
12=
9+
6+
7+
4
15
14
13
8
12
1
13=
4+
15+
14+
1=
34
Найдем сумму цифр в каждой строке
34
34
34
Слайд 1116
3
2
5
10
11
9
6
7
16+
3+
5+
2+
13+
11+
8=
7=
10+
11+
6+
4
15
14
13
8
12
1
10=
9+
6+
4+
15=
7+
12+
14+
1=
34
34
34
34
34
Найдем сумму цифр в каждом квадрате 2×2
Слайд 12
Так же бывают и другие виды магических фигур:
Магический треугольник
В кружках этого треугольника расставлены все девять значащих цифр так, чтобы
сумма их на каждой стороне составляла 20
Слайд 13Шестиконечная магическая звезда
У шестиконечной звезды все шесть рядов чисел имеют одну
4+6+7+9=26 11+6+8+1=26
4+8+12+2=26 11+7+5+3=26
9+5+10+2=26 1+12+10+3=26
Так же существуют восьмиконечная звезда.
Слайд 14Числовое колесо
Цифры от 1 до 9 размещены в
Слайд 15Магический циферблат
Циферблат разделён на 6 частей любой формы, - так, чтобы
имеющихся на каждом участке, была одна и та же.
Слайд 16Эту игру, также известную как магический квадрат придумал в 1783году
швейцарский математик
Игровое поле sudoku состоит из квадрата 9х9 клеток, разделенного на меньшие
квадраты 3х3 клеток. У головоломки всего одно правило: игроку необходимо
заполнить клетки цифрами от 1 до 9, таким образом, чтобы в каждой строке, в
каждом столбце и каждом квадрате 3х3 каждая цифра встречалась только один раз.
В некоторых ячейках уже в начале игры стоят числа, что может влиять на сложность
раскладки. Ключ к решению головоломки – это логика и внимание.
В середине ХХ века такие головоломки стали популярны в США, где их называли
Number place, а из Америки они попали в Японию, получив название sudoku (от
«су»- число, цифра и «доку»- позиция, место).
Настоящую популярность sudoku обрела в 80х годах ХХ века, когда японские
журналы начали публиковать эту головоломку на своих страницах. В 2005году
английские газеты также стали печатать sudoku, и это стало началом ее
триумфального шествия по всей Европе.
Есть несколько видов sudoku.
Судоку
Слайд 17Sudoku - диагональ. В этих sudoku цифры не повторяются не только
Например:
Слайд 18Sudoku - диагональ. В этих sudoku цифры не повторяются не только
Например:
Слайд 21Построение магического квадрата четвёртого порядка
Проведём диагонали квадрата 4 х 4
Вставляем в
Теперь ставим 16 в левый верхний угол и вписываем оставшиеся числа в порядке убывания.
Слайд 231. Магический квадрат
Расставьте 6 цифр от 1 до 9 так, чтобы
Решение:
Дано:
Слайд 242. Числовое колесо
Заполните фигуру так, чтобы сумма цифр в каждой паре
Решение:
Дано:
Слайд 25Список литературы
1. Аллан Рей, Вилльямс Мартин «Математика на пять». Издательство «АСТ
Москва, 1998г., стр. 36.
2. Доморяд А.П. «Математические развлечения и игры». Издательство
«ФИЗМАТИЗМ». Москва, 1958г., стр. 207 – 208.
3. Кордемский Б.А. «Математические завлекалки». Издательство «ОНИКС АЛЬЯНС
– В». Москва, 2000г., стр. 382 – 383.
4. Климченко Д.В. «Задачи по математике для любознательных». Издательство
«ПРОСВЕЩЕНИЕ». Москва, 1992г., стр.20, 63, 75.
5. Перельман Я.И. «Живая математика». Издательство «НАУКА». Москва, 1974., стр.
25, 57.
6. Перельман Я.И. «Занимательные задачи и опыты». Издательство «ДЕТСКАЯ
ЛИТЕРАТУРА». Москва, 1972г., стр. 350 – 351, 357 – 360.
7. Перельман Я.И. «Математика для любознательных». Издательство «РИМИС».
Москва, 2008г., стр. 99 – 107.
12. Постников М.М. «Магические квадраты». Издательство «НАУКА». Москва,
1969г., стр. 365.
8. Савин А.П «Математика от А до Я» - энциклопедический словарь для юношества.
Издательский дом «современная педагогика», издательство «ПЕДАГОГИКА -
ПРЕСС». Москва, 2001г., стр. 353 – 355.
9. Серпинский В. «Что мы знаем и чего не знаем о простых числах». Издательство
«ФИЗМАТИЗМ». Москва, 1963г., стр. 27 – 28.
10. Тресиддер Д. «Словарь символов». Издательство «ФАИР ПРЕСС». Москва,
2001г., стр. 141.
11. Якушева «Справочник школьника». Издательство «СЛОВО». Москва, 1995г.
12. Журнал «Судоку». Москва, 2010г., стр. 36 – 40.